- 1.34 MB
- 2021-06-26 发布
定州市 2017-2018 学年度第一学期期中考试
高二理科数学试卷
第Ⅰ卷(共 60 分)
一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1.双曲线 342
22
yx 的渐近线方程为( )
A. xy 2 B. xy 2 C. xy 2
2 D. xy 2
1
2.以下判断正确的是( )
A.命题“若 ba ,则
ba
11 ”为真命题 B.命题“ 01, 0
2
00 xxRx ”的
否定是“ 01, 2 xxRx ” C.“ )(2 Zkk ”是“函数
)sin()( xxf 是偶函数”的充要条件 D.命题“在 ABC 中,若 BA ,则
BA sinsin ”为假命题
3.分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量
的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有
甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多
少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180 钱,甲、乙、
丙三人一起出关,关税共100 钱,要按照各人带多少的比例进行交税,问三人各应付多少税?
则下列说法错误的是( )
A.甲应付
109
4151 钱 B.乙应付
109
2432 钱 C.丙应付
109
5616 钱 D.三
者中甲付的钱最多,丙付的钱最少
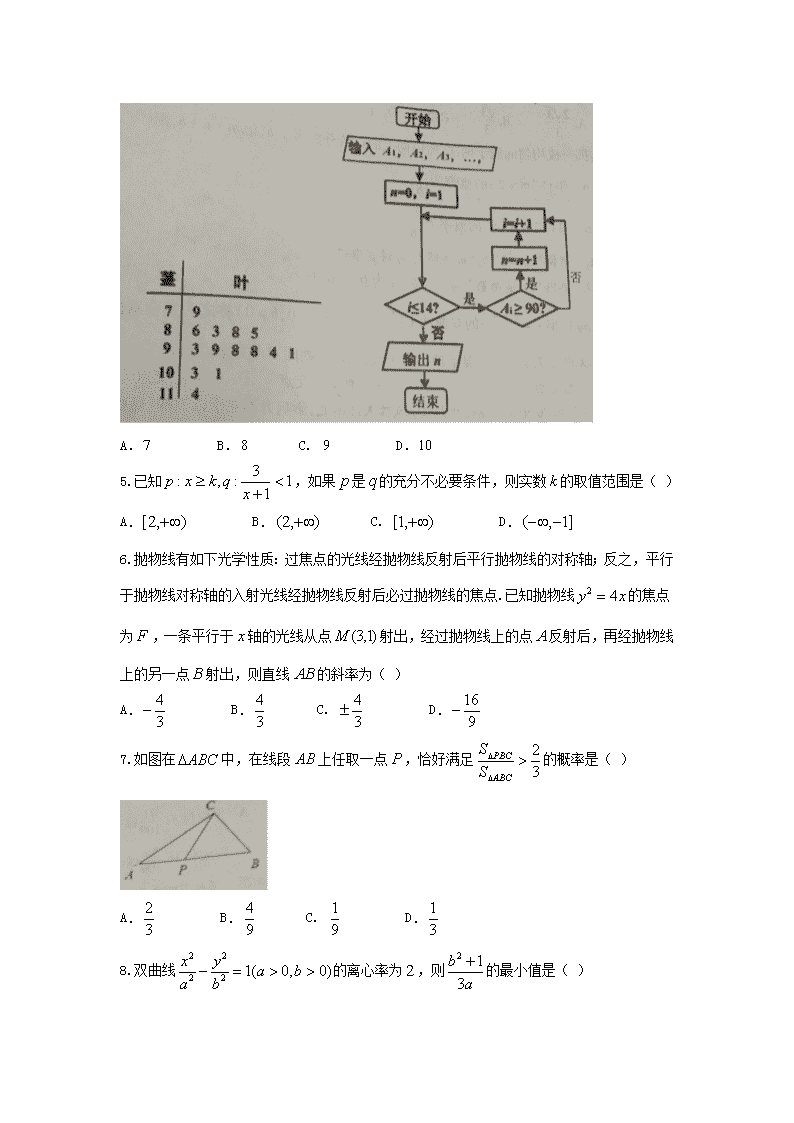
4.如图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到第14次的考试成绩依
次记为 1421 ,, AAA ,下图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,
那么算法流程图输出的结果是( )
A. 7 B.8 C. 9 D.10
5.已知 11
3:,:
xqkxp ,如果 p 是 q 的充分不必要条件,则实数 k 的取值范围是( )
A. ),2[ B. ),2( C. ),1[ D. ]1,(
6.抛物线有如下光学性质:过焦点的光线经抛物线反射后平行抛物线的对称轴;反之,平行
于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 xy 42 的焦点
为 F ,一条平行于 x 轴的光线从点 )1,3(M 射出,经过抛物线上的点 A 反射后,再经抛物线
上的另一点 B 射出,则直线 AB 的斜率为( )
A.
3
4 B.
3
4 C.
3
4 D.
9
16
7.如图在 ABC 中,在线段 AB 上任取一点 P ,恰好满足
3
2
ABC
PBC
S
S 的概率是( )
A.
3
2 B.
9
4 C.
9
1 D.
3
1
8.双曲线 )0,0(12
2
2
2
bab
y
a
x 的离心率为 2 ,则
a
b
3
12 的最小值是( )
A.
3
32 B.
3
3 C. 2 D.1
9.连掷一枚均匀的骰子两次,所得向上的点数分别为 ba, ,记 bam ,则( )
A.事件“ 2m ”的概率为
18
1 B.事件“ 11m ”的概率为
18
1 C.事件
“ 2m ”与“ 3m ”互为对立事件 D.事件“ m 是奇数”与“ ba ”互为互
斥事件
10.把离心率
2
15 e 的双曲线 )0,0(1: 2
2
2
2
bab
y
a
xC 称之为黄金双曲线,若以原
点为圆心,以虚半轴长为半径画圆O ,则圆O 与黄金双曲线( )
A.无交点 B.有1个交点 C. 有 2 个交点 D.有 4 个交点
11. 2015 年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》,某
记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年
龄在 ],19,15[],14,10[ ],24,20[
]34,30[],29,25[ 的爱看比例分别为 %%,30%,20%,18%,10 t ,现用这 5 个年龄段的中间值
x 代表年龄段,如12代表 17],14,10[ 代表 ]19,15[ ,根据前四个数据求得 x 关于爱看比例 y 的
线性回归方程为 )%68.4(
kxy ,由此可推测t 的值为( )
A.33 B.35 C. 37 D.39
12.设 21,FF 为椭圆 )0(1: 2
2
2
2
1 bab
y
a
xC 与双曲线 2C 的公共的左右焦点,它们在第一
象限内交于点 21, FMFM 是以线段 1MF 为底边的等腰三角形,若双曲线 2C 的离心率
]4,2
3[e ,则椭圆 1C 的离心率取值范围是( )
A. ]9
5,9
4[ B. ]8
3,0[ C. ]9
4,8
3[ D. ]1,9
5[
第Ⅱ卷(共 90 分)
二、填空题(每题 5 分,满分 20 分,将答案填在答题纸上)
13.原命题“若 3x ,则 0x ”的逆否命题是 .
14.比较两数的大小: )4(1000 )2(111111 .
15.抛物线 )0(22 ppyx 的焦点为 F ,其准线l 与双曲线 194
22
yx 相交于 BA、 两
点,若 FAB 为等边三角形,则 p 等于 .
16.下列命题中
①已知点 )0,3(),0,3( BA ,动点 P 满足 ||2|| PBPA ,则点 P 的轨迹是一个圆;
②已知 3||||),0,2(),0,2( PNPMNM ,则动点 P 的轨迹是双曲线右边一支;
③两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1;
④在平面直角坐标系内,到点 )1,1( 和直线 32 yx 的距离相等的点的轨迹是抛物线;
⑤设定点 )2,0(),2,0( 21 FF ,动点 P 满足条件 )0(4|||| 21 aaaPFPF ,则点 P 的轨
迹是椭圆.
正确的命题是 .
三、解答题 (本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演
算步骤.)
17. 已知命题 :p 直线 032 yx 与抛物线 )0(2 mmxy 没有交点;已知命题 :q 方程
125
22
m
y
m
x 表示双曲线;若 qp 为真, qp 为假,试求实数 m 的取值范围.
18. 已知抛物线 xy 2 与直线 )1( xky 相交于 BA, 两点.
(1)求证: OBOA ;
(2)当 AB 的弦长等于 10 时,求 k 的值.
19. 某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污
损,可见部分如图.
(1)求分数在 )60,50[ 的频率及全班人数;
(2)求分数在 )90,80[ 之间的频数,并计算频率分布直方图中 )100,80[ 间距形的高;
(3)若要从分数在 )100,80[ 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,
至少有一份分数在 )100,90[ 之间的概率.
20. 已知圆 4)1(: 22 yxC ,点 ),( ba .
(1)若 a 是从 3,2,1 三个数中任取的一个数,b 是从 2,1,0 三个数中任取的一个数,求点 ),( ba
在圆C 内的概率;
(2)若 a 是从区间 ]3,1[ 任取的一个数,b 是从区间 ]2,0[ 任取的一个数,求点 ),( ba 在圆C
外的概率.
21. 已知 21,FF 是椭圆 )0(12
2
2
2
bab
y
a
x 的左右焦点,O 为原点,P )5
5,2( 在椭圆
上,线段 1PF 与 y 轴的交点 N 满足 )(2
1
1
OFOPON .
(1)求椭圆的标准方程;
(2)过椭圆右焦点 2F 作直线l 交椭圆于 BA, 两点,交 y 轴于 M 点,若
2221 , BFMBAFMA ,求 21 .
22.已知 21,FF 分别是椭圆 )0(1: 2
2
2
2
bab
y
a
xE 的左、右焦点,离心率为
2
1 , NM, 分
别是椭圆的上、下顶点, 222
NFMF .
(1)求椭圆 E 的方程;
(2)过 )2,0(M 作直线与 E 交于 BA, 两点,求三角形 AOB 面积的最大值(O 是坐标原点).
试卷答案
一、选择题
1-5: ACBCD 6-10:ADADD 11、12:BC
二、填空题
13.若 0x ,则 3x 14. 15. 23 16.①②③
三、解答题
17.解:若直线 032 yx 与抛物线 )0(2 mmxy 没有交点,
由 032 yx 得 32 yx ,代入 )0(2 mmxy 得 )32(2 ymy ,
得 0322 mmyy .
则由 0124 2 mm ,解得 30 m ,
若方程 125
22
m
y
m
x 表示双曲线,则 0)25( mm ,
得 0m 或
2
5m ,
若 qp 为真, qp 为假,则 qp, 一真一假,
若 p 真 q 假,则
2
50
30
m
m
得
2
50 m ,
若 p 假 q ,则
02
5
03
mm
mm
或
或
得 0m 或 3m ,
综上所述 m 的取值范围是 0m 或 3m 或
2
50 m .
18.解:(1)由方程组
)1(
2
xky
xy ,消去 x 后,整理得 02 kyky ,
设 0),,(),,( 2211 kyxByxA ,由韦达定理知: 121 yy .
因为 BA、 在抛物线 xy 2 上, 2
2
21
2
1 , xyxy ,所以 21
2
2
2
1 xxyy .
则 11
212
2
1
1
yyx
y
x
ykk OBOA ,
所以 OBOA .
(2)连接 AB ,由(1)知 1,1
2121 yykyy ,
)1(4)1(114)(11||11|| 2
221
2
212212
kkyyyykyykAB
104111 22
kk
则 10)41)(11( 22
kk
即 06)1(5)1( 2
2
2
kk
得 0)11)(61( 22
kk
所以 1,11
2 kk .
19.解:(1)分数在 )60,50[ 的频率为 08.010008.0 ,
由茎叶图知:分数在 )60,50[ 之间的频数为 2 ,
全班人数为 2508.0
2 .
(2)分数在 )90,80[ 之间的频数为 32225 ;
频率分布直方图中 )90,80[ 间的矩形的高为 012.010/25
3 .
(3)将 )90,80[ 之间的 3 个分数编号为 )100,90[,,, 321 aaa 之间的 2 个分数编号为 21,bb ,在
)100,80[ 之间的试卷中任取两份的基本事件为:
),,(),,( 3121 aaaa ),,(),,(),,(),,(),,( 2212322111 babaaababa ),,(),,( 2313 baba
),( 21 bb 共10个,其中,至少有一个在 )100,90[ 之间的基本事件有 7 个,
故至少有一份分数在 )100,90[ 之间的概率是 7.010
7 .
20.解:(1)用数对 ),( ba 表示基本事件,则其所有可能结果有:
),2,1(),1,1(),0,1( ),0,3(),2,2(),1,2(),0,2(
)2,3(),1,3( 共 9 个.
事件 A {点 ),( ba 在圆C 内},
其结果为: )1,2(),0,2(),1,1(),0,1( 共 4 个,
所以
9
4)( AP .
(2)所有可能结果 }20
31|),{(
b
aba 表示的区域图中正方形 ABCD ,事件 {点
),( ba 在圆C 外}表示的区域为图中阴影部分,
所以
4122
24
122
)(
2
BP .
21.解:(1)因为 )(2
1
1
OFOPON 知 N 为 1PF 中点,而 O 又为 21FF 中点,所以ON 为
PFF 21 的中位线,又由于 21FFON ,所以 211 FFPF ,由 P 坐标可知 )0,2(2F ,所以
PFFRtFF 2121 ),0,2(),0,2( 中,由勾股定理得
5
59|| 1 PF ,又因为
5
5|| 2 PF ,所以
552||||2 21 aPFPFa .
易得椭圆的标准方程为: 15
2
2
yx
(2)设 ),0(),,(),,( 32211 yMyxByxA 显然直线l 存在斜率,
故设l 的方程为: )2( xky ,
由
15
)2(
2
2
yx
xky
联立得 052020)15( 2222 kxkxk
15
520,15
20,0 2
2
212
2
21
k
kxxk
kxx ,
又
2221 , BFMBAFMA ,将各点坐标代入得:
2
2
2
1
1
1 2,2 x
x
x
x
10
415
520)15
20(2
15
5202)15
20(2
4)(2
2)(2
22
2
2
2
2
2
2
2
2
2121
2121
2
2
1
1
21
k
k
k
k
k
k
k
k
xxxx
xxxx
x
x
x
x .
22. 解:(1)由题知, ),0(),,0(),0,(2 bNbMcF
22,2 2222
22
babcNFMF ,①
2222
4
3,2
1,2
1 acabaca
ce ,②
①②联立解得 3,4 22 ba ,
椭圆 E 的方程为 134
22
yx .
(2)设 ),(),,( 2211 yxByxA ,显然直线 AB 斜率存在,设其方程为 2 kxy 。代入
01243 22 yx 整理得 0416)43( 22 kxxk ,
则 0)43(44)16( 22 kk ,即
4
12 k ,
221221 43
4,43
16
kxxk
kxx
,
]4))[(1(||| 21
2
21
2 xxxxkAB
22
22
2
2
2
2
)34(
)14)(1(48]43
44)43
16)[(1(
k
kk
kk
kk
所以O 到l 的距离
21
2
k
d
,
所以三角形 AOB 面积 22
2
222
22
)34(
)14(34
1
2
)34(
)14)(1(48
2
1)(
k
k
kk
kkkS ,
设 014 2 kt ,所以 3
8162
34
816
34
)4(
34)( 2
ttttt
tts ,
当且仅当
tt 16 ,即 4t ,即 414 2 k ,即
2
5k 时取等号,
所以 AOB 面积最大值为 3 .