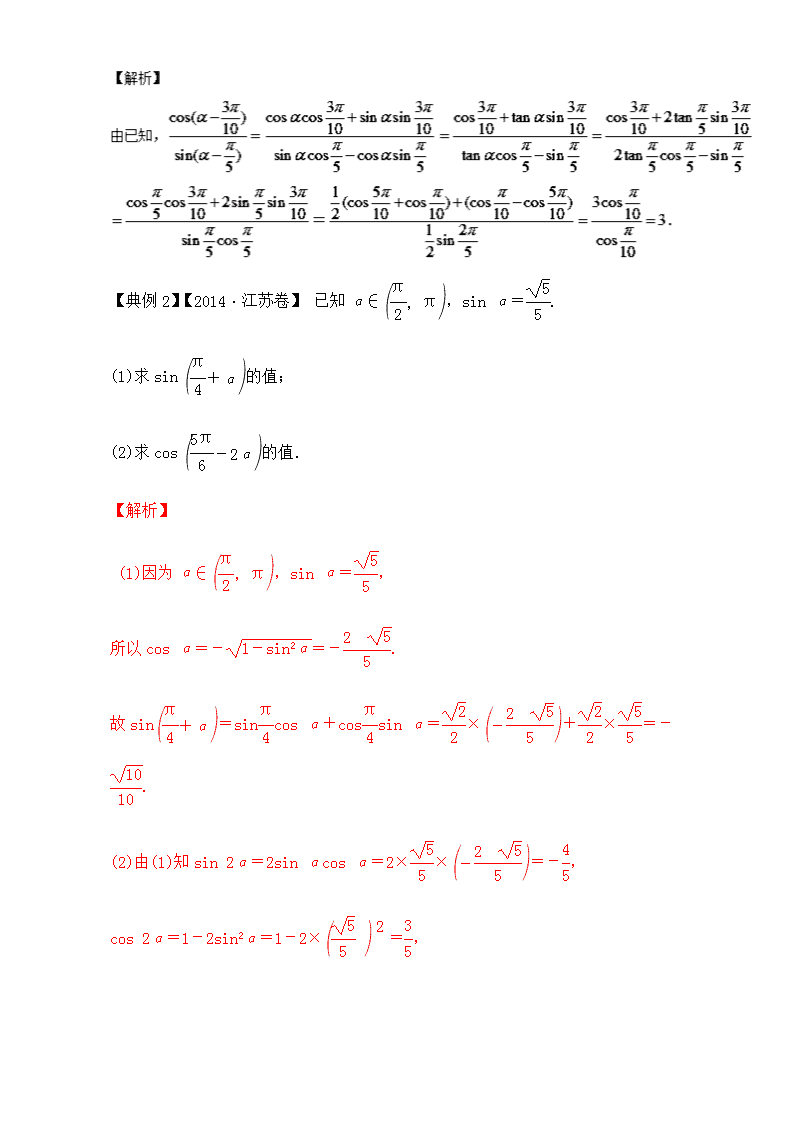- 186.00 KB
- 2021-06-26 发布
热点题型五 两角和(差)的正弦、余弦及正切
【基础知识整合】
1.两角和与差的余弦、正弦、正切公式
cos(α-β)=cos αcos β+sin αsin β (C(α-β))
cos(α+β)=cos αcos β-sin αsin β (C(α+β))
sin(α-β)=sin αcos β-cos αsin β (S(α-β))
sin(α+β)=sin αcos β+cos αsin β (S(α+β))
tan(α-β)= (T(α-β))
tan(α+β)= (T(α+β))
2.二倍角公式
sin 2α=2sin αcos α;
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;
tan 2α=.
3.公式的逆用、变形等
(1)tan α±tan β=tan(α±β)(1∓tan αtan β);
(2)cos2α=,sin2α=;
(3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=sin.
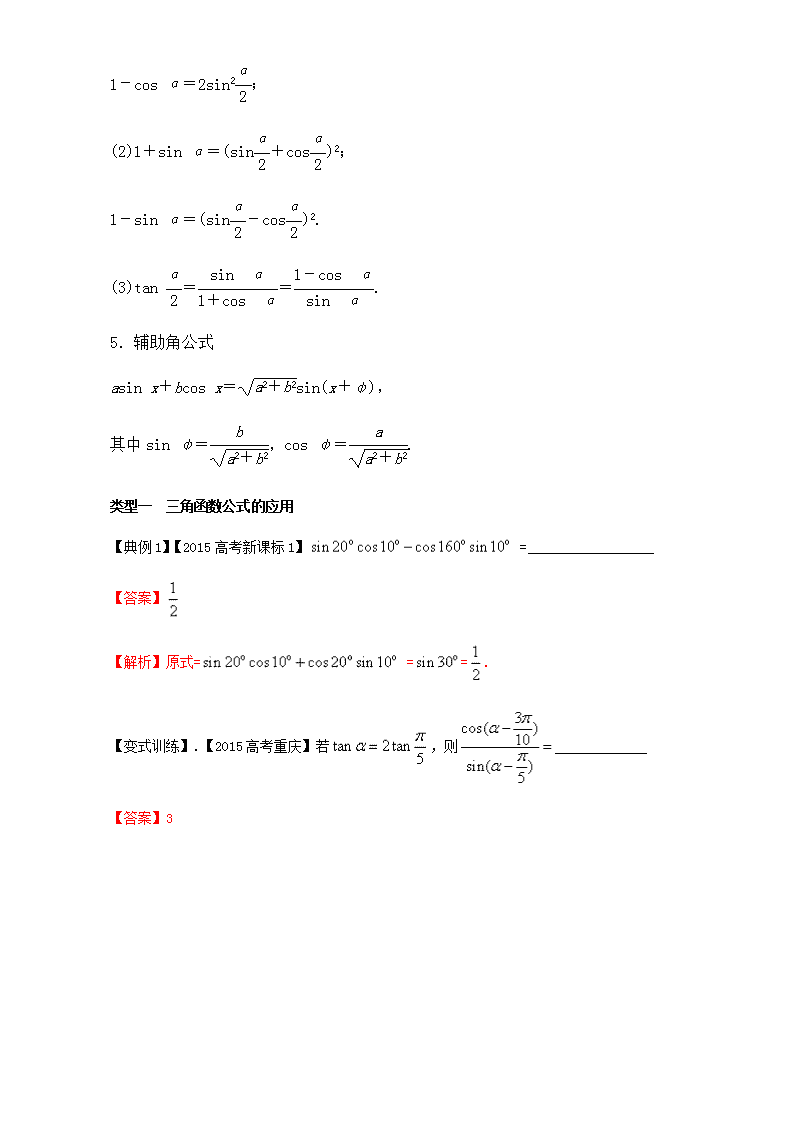
4.公式的常见变形
(1)1+cos α=2cos2;
1-cos α=2sin2;
(2)1+sin α=(sin+cos)2;
1-sin α=(sin-cos)2.
(3)tan ==.
5.辅助角公式
asin x+bcos x=sin(x+φ),
其中sin φ=,cos φ=.
类型一 三角函数公式的应用
【典例1】【2015高考新课标1】 =
【答案】
【解析】原式= ==.
【变式训练】.【2015高考重庆】若,则
【答案】3
【典例2】【2014·江苏卷】 已知α∈,sin α=.
(1)求sin的值;
(2)求cos的值.
【解析】
(1)因为α∈,sin α=,
所以cos α=-=-.
故sin=sincos α+cossin α=×+×=-.
(2)由(1)知sin 2α=2sin αcos α=2××=-,
cos 2α=1-2sin2α=1-2×=,
所以cos=coscos 2α+sinsin 2α=×+×=-.
【变式训练】【2014·新课标全国卷Ⅱ】 函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为________.
【答案】1
【解析】函数f(x)=sin(x+2φ)-2sin φcos(x+φ)
=sin【(x+φ)+φ】-2sin φcos(x+φ)
=sin(x+φ)cos φ-cos(x+φ)sin φ=sin x,
故其最大值为1.
【解题技巧】
(1)两角和与差的三角函数公式可看作是诱导公式的推广,可用α、β的三角函数表示α±β的三角函数,在使用两角和与差的三角函数公式时,特别要注意角与角之间的关系,完成统一角和角与角转换的目的.
(2)运用两角和与差的三角函数公式时,不但要熟练、准确,而且要熟悉公式的逆用及变形,如tan α+tan β=tan(α+β)·(1-tan αtan β) 和二倍角的余弦公式的多种变形等.
类型二、三角函数式的化简与给角求值
【典例3】 【2016高考新课标2理数】若,则( )
(A) (B) (C) (D)
【答案】D
考点:三角恒等变换.
【思路点拨】三角函数的给值求值,关键是把待求角用已知角表示:
(1)已知角为两个时,待求角一般表示为已知角的和或差.
(2)已知角为一个时,待求角一般与已知角成“倍的关系”或“互余互补”关系.
【变式训练】
【2015江苏高考,8】已知,,则的值为_______.
【答案】3
【解析】
【考点定位】两角差正切公式
【思路点拨】善于发现角之间的差别与联系,合理对角拆分,完成统一角和角与角转换的目的是三角函数式的求值的常用方法. 三角函数求值有三类(1)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.(2)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.(3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,确定角.
【一题多解】
【2015高考四川,理12】 .
【答案】.
【考点定位】三角恒等变换及特殊角的三角函数值.
有.第二种方法是直接凑为特殊角,利用特殊角的三角函数值求解.
【思路点拨】这是一个来自于课本的题,这告诉我们一定要立足于课本.首先将两个角统一为一个角,然后再化为一个三角函数一般地,有.第二种方法是直接凑为特殊角,利用特殊角的三角函数值求解.
【解题技巧】
(1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子结构与特征.
(2)对于给角求值问题,往往所给角都是非特殊角,解决这类问题的基本思路有:
①化为特殊角的三角函数值;
②化为正、负相消的项,消去求值;
③化分子、分母出现公约数进行约分求值.
类型三、三角函数的给值求值、给值求角
【典例4】【2015高考广东】已知.
(1)求的值;
(2)求的值.
【答案】(1);(2).
【典例5】【2015·常州一模】已知α,β均为锐角,且sin α=,tan(α-β)=-.
(1)求sin(α-β)的值;
(2)求cos β的值.
【解析】 (1)∵α,β∈,从而-<α-β<.
又∵tan(α-β)=-<0,∴-<α-β<0.
∴sin(α-β)=-.
(2)由(1)可得,cos(α-β)=.
∵α为锐角,且sin α=,∴cos α=.
∴cos β=cos【α-(α-β)】
=cos αcos(α-β)+sin αsin(α-β)
=×+×
=.
【变式训练1】【2015·青岛质量检测】设α为锐角,若cos=,则sin的值为________.
【答案】
【变式训练2】【2014·华中师大模拟】已知α,β∈(0,π),且tanα=2,cosβ=-.
(1)求cos2α的值;
(2)求2α-β的值.
【解析】(1)cos2α=cos2α-sin2α====-.
(2)因为α∈(0,π),且tanα=2,所以α∈(0,).
又cos2α=-<0,故2α∈(,π),sin2α=.
由cosβ=-,β∈(0,π),
得sinβ=,β∈(,π).
所以sin(2α-β)=sin2αcosβ-cos2αsinβ=×(-)-(-)×=-.
又2α-β∈(-,),所以2α-β=-.
【典例6】【2015·重庆】已知函数f(x)=sinsin x-cos2x.
(1)求f(x)的最小正周期和最大值;
(2)讨论f(x)在上的单调性.
【思维点拨】 (1)讨论形如y=asin ωx+bcos ωx型函数的性质,一律化成y=sin(ωx+φ)型的函数.
(2)研究y=Asin(ωx+φ)型函数的最值、单调性,可将ωx+φ视为一个整体,换元后结合y=sin x的图象解决.
【规范解答】
【解析】 (1)f(x)=sinsin x-cos2x
=cos xsin x-(1+cos 2x)=sin 2x-cos 2x-=sin-,
因此f(x)的最小正周期为π,最大值为
(2)当x∈时,0≤2x-≤π,
从而当0≤2x-≤,
即≤x≤时,f(x)单调递增,
当≤2x-≤π,即≤x≤时,f(x)单调递减.
综上可知,f(x)在上单调递增;
在上单调递减.
【温馨提醒】
(1)讨论三角函数的性质,要先利用三角变换化成y=Asin(ωx+φ),φ的确定一定要准确.
(2)将ωx+φ视为一个整体,设ωx+φ=t,可以借助y=sin t的图象讨论函数的单调性、最值等.
【解题技巧】
(1)解题中注意变角,①当“已知角”有两个时,一般把“所求角”表示为两个“已知角”的和或差的形式;②当“已知角”有一个时,此时应着眼于“所求角”与 “已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”;
(2)通过求角的某种三角函数值来求角,在选取函数时,遵照以下原则:①已知正切函数值,选正切函数;②已知正、余弦函数值,选正弦或余弦函数;若角的范围是,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为,选正弦较好.