- 81.50 KB
- 2021-06-25 发布
课时分层训练(十一)
A组 基础达标
(建议用时:30分钟)
1.(2017·如皋市高三调研一)已知函数f(x)=e3x-6-3x,求函数y=f(x)的极值.
[解] 由f′(x)=3e3x-6-3=3(e3x-6-1)=0,得x=2.
x
(-∞,2)
2
(2,+∞)
f′(x)
-
0
+
f(x)
所以,由上表可知f(x)极小值=f(2)=-5,
所以f(x)在x=2处取得极小值-5,无极大值.
2.(2017·镇江期中) 已知函数f(x)=e2x-1-2x.
(1)求函数f(x)的导数f′(x);
(2)证明:当x∈R时,f(x)≥0 恒成立. 【导学号:62172356】
[解] (1)函数f(x)=e2x-1-2x,定义域为R,
f′(x)=e2x-1×(2x-1)′-2=2e2x-1-2.
(2)由题意f′(x)=2e2x-1-2,x∈R ,
x,f′(x),f(x)在x∈R上变化如下表:
x
f′(x)
-
0
+
f(x)
极小值
当x=时f(x)取得极小值也是最小值,
而f=0,
故f(x)≥0恒成立.
3.(2016·北京高考)设函数f(x)=xea-x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.
(1)求a,b的值;
(2)求f(x)的单调区间.
[解] (1)因为f(x)=xea-x+bx,
所以f′(x)=(1-x)ea-x+b.
依题设,即
解得
(2)由(1)知f(x)=xe2-x+ex.
由f′(x)=e2-x(1-x+ex-1)及e2-x>0知,f′(x)与1-x+ex-1同号.
令g(x)=1-x+ex-1,则g′(x)=-1+ex-1.
所以,当x∈(-∞,1)时,g′(x)<0,g(x)在区间(-∞,1)上单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)在区间(1,+∞)上单调递增.
故g(1)=1是g(x)在区间(-∞,+∞)上的最小值,
从而g(x)>0,x∈(-∞,+∞).
综上可知,f′(x)>0,x∈(-∞,+∞),故f(x)的单调递增区间为(-∞,+∞).
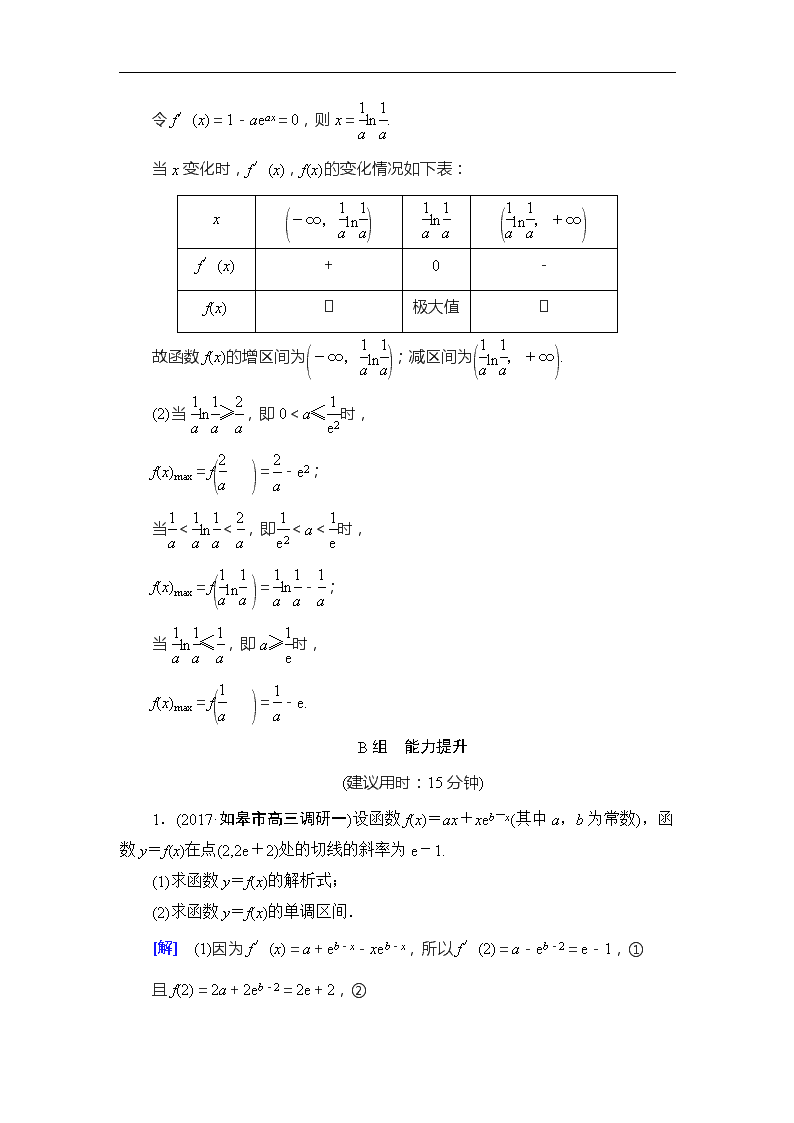
4.已知函数f(x)=x-eax(a>0).
(1)求函数f(x)的单调区间;
(2)求函数f(x)在上的最大值. 【导学号:62172357】
[解] (1)f(x)=x-eax(a>0),则f′(x)=1-aeax,
令f′(x)=1-aeax=0,则x=ln.
当x变化时,f′(x),f(x)的变化情况如下表:
x
ln
f′(x)
+
0
-
f(x)
极大值
故函数f(x)的增区间为;减区间为.
(2)当ln≥,即0<a≤时,
f(x)max=f=-e2;
当<ln<,即<a<时,
f(x)max=f=ln-;
当ln≤,即a≥时,
f(x)max=f=-e.
B组 能力提升
(建议用时:15分钟)
1.(2017·如皋市高三调研一)设函数f(x)=ax+xeb-x(其中a,b为常数),函数y=f(x)在点(2,2e+2)处的切线的斜率为e-1.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
[解] (1)因为f′(x)=a+eb-x-xeb-x,所以f′(2)=a-eb-2=e-1,①
且f(2)=2a+2eb-2=2e+2,②
由①②得a=e,b=2,所以f(x)=ex+xe2-x.
(2)f′(x)=e+e2-x-xe2-x,
由f″(x)=-e2-x-e2-x+xe2-x=e2-x(x-2)=0,得x=2.
当x变化时,f″(x),f′(x)的变化情况如下表:
x
(-∞,2)
2
(2,+∞)
f″(x)
-
0
+
f′(x)
f′(x)最小值=e-1>0,即f′(x)>0恒成立.
所以f(x)的单调增区间为(-∞,+∞).
2.已知函数f(x)=(x-k)2e.
(1)求f(x)的单调区间;
(2)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围.
[解] (1)由f(x)=(x-k)2e,得
f′(x)=(x2-k2)e,
令f′(x)=0,得x=±k,
若k>0,当x变化时,f(x)与f′(x)的变化情况如下:
x
(-∞,-k)
-k
(-k,k)
k
(k,+∞)
f′(x)
+
0
-
0
+
f(x)
4k2e-1
0
所以f(x)的单调递增区间是(-∞,-k)和(k,+∞),单调递减区间是(-k,k).
若k<0,当x变化时,f(x)与f′(x)的变化情况如下:
x
(-∞,k)
k
(k,-k)
-k
(-k,+∞)
f′(x)
-
0
+
0
-
f(x)
0
4k2e-1
所以f(x)的单调递减区间是(-∞,k)和(-k,+∞),单调递增区间是(k,-k).
(2)当k>0时,因为f(k+1)=e>,
所以不会有∀x∈(0,+∞),f(x)≤.
当k<0时,由(1)知f(x)在(0,+∞)上的最大值是f(-k)=.
所以∀x∈(0,+∞),f(x)≤等价于f(-k)=≤,
解得-≤k<0.
故当∀x∈(0,+∞),f(x)≤时,k的取值范围是.
3.已知函数f(x)=ex-e-x-2x.
(1)讨论f(x)的单调性;
(2)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值.
[解] (1)f′(x)=ex+e-x-2≥0,等号仅当x=0时成立.
所以f(x)在(-∞,+∞)单调递增.
(2)g(x)=f(2x)-4bf(x)
=e2x-e-2x-4b(ex-e-x)+(8b-4)x,
g′(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]
=2(ex+e-x-2)(ex+e-x-2b+2).
①当b≤2时,g′(x)≥0,等号仅当x=0时成立,
所以g(x)在(-∞,+∞)上单调递增.
而g(0)=0,所以对任意x>0,g(x)>0.
②当b>2时,若x满足20).
当a≤0时,f′(x)>0,f′(x)没有零点;
当a>0时,设u(x)=e2x,v(x)=-,
因为u(x)=e2x在(0,+∞)上单调递增,v(x)=-在(0,+∞)上单调递增,
所以f′(x)在(0,+∞)上单调递增.
又f′(a)>0,当b满足00时,f′(x)存在唯一零点.
(2)证明:由(1),可设f′(x)在(0,+∞)上的唯一零点为x0,当x∈(0,x0)时,f′(x)<0;
当x∈(x0,+∞)时,f′(x)>0.
故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,所以当x=x0时,f(x
)取得最小值,最小值为f(x0).
由于2e2x0-=0,
所以f(x0)=+2ax0+aln≥2a+aln .
故当a>0时,f(x)≥2a+aln .