专题47+空间中的垂直关系（检测）-2019年高考数学（文）名师揭秘之一轮总复习 53页

‎【学习目标】‎ ‎1.熟练掌握直线和平面垂直的定义，判定定理和性质定理，并能依据条件，灵活运用.‎ ‎2.掌握两个平面垂直的判定定理、性质定理，并能进行论证和解决有关问题.‎ ‎3.熟悉线线垂直、线面垂直、面面垂直的转化.强化空间垂直感觉.‎ ‎【知识要点】‎ ‎1．直线与平面垂直的判定 ‎(1)(定义)如果一条直线和平面内_______________都垂直，那么这条直线和这个平面垂直．‎ ‎(2)判定定理：如果一条直线和一个平面内的_________________都垂直，那么这条直线垂直于这个平面．用符号语言表示为：m⊂α，n⊂α，m∩n＝B，l⊥m，l⊥n⇒l⊥α.‎ ‎(3)如果两条平行线中的一条___________一个平面，那么另一条也垂直于这个平面．用符号语言表示为：___________________．‎ ‎(4)(面面垂直的性质定理)如果两个平面垂直，那么在一个_______________垂直于它们交线的直线垂直于另一个平面．‎ ‎(5)(两平面平行的性质定理)如果两个平面平行，那么与其中一个平面_____________的直线也与另一个平面垂直．‎ ‎(6)如果两个相交平面都垂直于第三个平面，那么它们的______________也垂直于第三个平面．‎ ‎2．直线和平面垂直的性质 如果两条不重合的直线____________于一个平面，那么这两条直线平行，即a⊥α，b⊥α⇒a∥b.‎ ‎3．两平面垂直的判定 ‎(1)(定义)两个平面相交，如果所成的二面角是_________________，那么这两个平面互相垂直；‎ ‎(2)(判定定理)如果一个平面_______________另一个平面的一条_____________，那么这两个平面互相垂直．即_______________，a⊂α⇒α⊥β.‎ ‎4．两平面垂直的性质 如果两个平面垂直，那么在一个平面内垂直于它们____________的直线垂直于另一个平面．即α⊥β，α∩β＝l，_____________，a⊂α⇒a⊥β.‎ ‎【高考模拟】‎ 一、单选题 ‎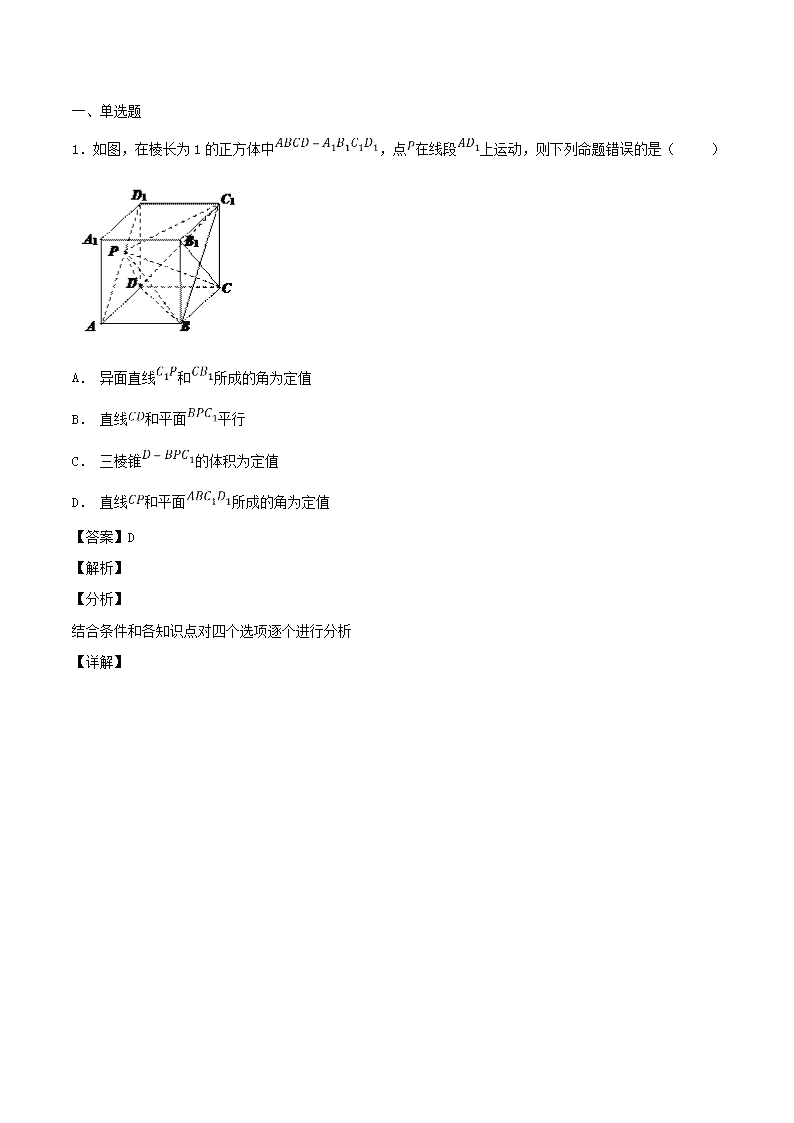1．如图，在棱长为1的正方体中，点在线段上运动，则下列命题错误的是（ ）‎ A． 异面直线和所成的角为定值 B． 直线和平面平行 C． 三棱锥的体积为定值 D． 直线和平面所成的角为定值 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 结合条件和各知识点对四个选项逐个进行分析 ‎【详解】‎ ‎，而平面 点到平面的距离即为点到该平面的距离，‎ 三棱锥的体积为定值，故正确 ‎，由线面夹角的定义，令与的交点为，可得即为直线和平面所成的角，当移动时这个角是变化的，故错误 故选 ‎【点睛】‎ 本题考查了异面直线所成角的概念、线面平行及线面角等，三棱锥的体积的计算可以进行顶点轮换及线面平行时，直线上任意一点到平面的距离都相等这一结论，即等体积法的转换。‎ ‎2．三棱锥中，则在底面的投影一定在三角形的（ ）‎ A． 内心 B． 外心 C． 垂心 D． 重心 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先画出图形，过作平面，垂足为，连接并延长交于，连接，可推出，结合，根据线面垂直定理，得证，同理可证，从而可得出结论．‎ ‎【详解】‎ 过作平面，垂足为，连接并延长交于，连接.‎ 又，‎ 平面 又平面 ‎，同理 是三角形的垂心.‎ 故选C.‎ ‎【点睛】‎ 本题考查了三角形垂心的性质，考查了直线和平面垂直的判定定理和性质定理，以及直线和直线垂直的判定，在证明线线垂直时，其常用的方法是利用证明线面垂直，在证明线线垂直，同时熟记线面位置关系的判定定理和性质定理是解答的关键.‎ ‎3．如图，在三棱锥中，⊥底面，，则直线与平面所成角的大小为 A． B． ‎ C． D． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据⊥底面，判断出为直线与平面所成角，利用三角形为等腰直角三角形求解 ‎【详解】‎ ‎【点睛】‎ 求解线面角的步骤：先找出线面角，再证明线面角，最后求解线面角。‎ ‎4．如图，在中，，为所在平面外一点，，则四面体中直角三角形的个数为 (　）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据线面垂直得线线垂直，根据线线垂直确定直角三角形的个数.‎ ‎【详解】‎ ‎【点睛】‎ 本题考查线面垂直判定与性质，考查基本分析论证能力.‎ ‎5．四棱锥中，底面是边长为的正方形，若四条侧棱相等，且该四棱锥的体积，则二面角的大小为 A． B． C． D． ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由体积和底面边长分别求出四棱锥的高和斜高，找出二面角的平面角解三角形 ‎【详解】‎ 如图，连接，交于点 四条侧棱相等 面，取的中点，则为二面角的平面角 则 则 故选 ‎【点睛】‎ 要求二面角的大小就要先找出二面角的平面角，然后解三角形，本题中条件给出四条侧棱相等则可以判定顶点的射影在底面中心，然后求解 ‎6．如图，在三棱锥中，侧面底面BCD，，，，，直线AC与底面BCD所成角的大小为　　‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 取BD中点,可证，为直线AC与底面BCD所成角。‎ ‎【详解】‎ 取BD中点，由，，又侧面底面BCD，所以。‎ 所以为直线AC与底面BCD所成角。‎ ‎,所以。选A.‎ ‎【点睛】‎ 本题考查线面角，用几何法求线面角要一作、二证、三求，要有线面垂直才有线面角。‎ ‎7．如图, 在正方体中, , 过直线的平面平面,则平面截该正方体所得截面的面积为（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由正方体结构特征，易得体对角线，取中点，则为所求截面，再进行求解即可.‎ ‎【详解】‎ 如图所示，连接交于，取中点，连接、、和，‎ ‎【点睛】‎ 本题考查面面垂直的判定，考查正方体的结构特征，借助正方体的结构正确的判定垂直平面的位置是解题关键.‎ ‎8．如图，已知平面，，、是直线上的两点，、是平面内的两点，且，，，，．是平面上的一动点，且直线，与平面所成角相等，则二面角的余弦值的最小值是（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 为所求的二面角的平面角，由得出，求出在内的轨迹，根据轨迹的特点求出的最大值对应的余弦值 ‎【详解】‎ ‎，‎ 在平面内，以为轴，以的中垂线为轴建立平面直角坐标系 则，设 ‎，整理可得：‎ 在内的轨迹为为圆心，以为半径的上半圆 平面平面，，‎ 为二面角的平面角，‎ 当与圆相切时，最大，取得最小值 此时 故选 ‎【点睛】‎ 本题主要考查了二面角的平面角及其求法，方法有：定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等，依据题目选择方法求出结果。‎ ‎9．已知三棱锥的四个顶点都在球的球面上，平面，是边长为2的等边三角形，若球的体积为，则直线与平面所成角的正切值为 A． B． C． D． ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 取的中点，则为所求线面角，利用勾股定理求出即可得出答案．‎ ‎【详解】‎ ‎【点睛】‎ 本题考查了棱锥与球的位置关系，属于中档题．‎ ‎10．如图，矩形中，，是线段（不含点）上一动点，把沿折起得到，使得平面平面，分别记，与平面所成角为，平面与平面所成锐角为，则（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由题意画出图形，作出与平面所成角为，平面与平面所成锐角为，分别求出和，与平面所成角为则答案可求．‎ ‎【详解】‎ 如图，过作，在中，由，可得． 由等积法可得，则 ‎∵平面平面，且，可得平面， 则． 过作，垂足为，连接，则为平面与平面所成的锐角． ∵到的距离 ‎ ‎ 即 ． 故选：A．‎ ‎【点睛】‎ 本题考查空间中直线与平面、平面与平面所成角的求法，考查空间想象能力与逻辑思维能力，是中档题．‎ ‎11．如图，在三棱柱中，各棱长相等，侧棱垂直于底面，点是侧面的中点，则与平面所成角的大小是（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 取BC的中点E，连接AE，DE，则平面，从而为所求角，在中计算即可.‎ ‎【详解】‎ 取BC的中点E，连接AE，DE，‎ 则平面，‎ 为与平面所成的角，‎ 设三棱柱的棱长为1，则，‎ ‎，‎ ‎.‎ 故选：A.‎ ‎【点睛】‎ 本题考查了线面角的计算，作出所求的线面角是解题的关键，属于基础题.‎ ‎12．如图，正方体的棱长为1，线段上有两个动点，且；则下列结论错误的是（）.‎ A． B． ‎ C． 三棱锥 的体积为定值 D． △ 的面积与△的面积相等 ‎【答案】D ‎【解析】‎ ‎【详解】‎ 分析：在正方体中，点到的距离为，而到的距离为，因此可以判断D是错误的.‎ 详解：在正方体中，平面，‎ 而平面，故，故A正确.‎ 又平面，因此平面，故B正确.‎ 当变化时，三角形的面积不变，点到平面的距离就是到平面的距离，它是一个定值，故三棱锥的体积为定值（此时可看成三棱锥的体积），故C正确. ‎ 在正方体中，点到的距离为，而到的距离为， D是错误的.‎ 综上，选D. ‎ 点睛：在三棱锥的体积的计算过程中，我们要选择合适的顶点和底面，使得顶点到底面的距离容易求得.‎ ‎13．对于命题：①平行于同一直线的两个平面平行；②平行于同一平面的两个平面平行；③垂直于同一直线的两直线平行；④垂直于同一平面的两直线平行.其中正确的个数有( )‎ A． 1 个 B． 2个 C． 3个 D． 4个 ‎【答案】B ‎【解析】分析：通过找出①③的反例，判断正误；利用平面平行的性质与判定判断②的正误；利用直线垂直平面的性质判定④的正误，得到正确结果.‎ 点睛：本题考查了用文字语言叙述的空间中平行和垂直关系的判定，是基础题，熟练掌握空间中的线线、线面、面面的位置关系是解题的关键.‎ ‎14．在四面体ABCD中，已知棱AC的长为，其余各棱长都为1，则二面角A-CD-B的余弦值为　 (　 )‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】分析：根据图像，连接的中点为，的中点为，由题意，，则为二面角A-CD-B的平面角，在中根据余弦定理求解即可。‎ 详解：将四面体ABCD放入三棱锥进行研究，如图根据题意，设的中点为，的中点为，连接 ‎，所以，则，，则为二面角A-CD-B的平面角，，，由余弦定理可知，故选C。‎ 点睛：用几何方法求二面角的大小的步骤：1、先找出二面角的平面角。‎ ‎2、证明二面角的平面角。3、求解二面角的平面角。‎ ‎15．在正方体中, 与垂直的是(　　)‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】分析：先证明BD⊥平面,再证明⊥BD.‎ 详解：因为BD⊥AC,BD⊥,,‎ 所以BD⊥平面，所以⊥BD.故答案为：A.‎ 点睛：本题主要考查线面垂直的判定和性质，意在考查学生对这些知识的掌握水平和空间想象转化能力，属于基础题.‎ ‎16．如图，P是正四面体V-ABC的面VBC上一点，点P到平面ABC距离与到点V的距离相等，则动点P的轨迹是( )‎ A． 直线 B． 抛物线 C． 离心率为的椭圆 D． 离心率为3的双曲线 ‎【答案】C ‎【解析】分析：由题设条件将点P到平面ABC距离与到点V的距离相等转化成在面VBC中点P到V的距离与到定直线BC的距离比是一个常数，依据圆锥曲线的第二定义判断出其轨迹的形状．‎ 点睛：（1）本题主要考查二面角、椭圆的定义、轨迹方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．(2)解答本题的关键是联想到圆锥曲线的第二定义.‎ ‎17．把边长为的正方形沿对角线折起，当、两点距离为时，二面角的大小为（ ）‎ A． 30° B． 45° C． 60° D． 90°‎ ‎【答案】D ‎【解析】分析：设正方形对角线交点为，可证明为二面角的平面角，‎ 折起后的图形中，，又知，由勾股定理可得结果.‎ 详解：‎ 点睛：本题主要考查二面角的求法，属于中档题. 求二面角的大小既能考查线线垂直关系，又能考查线面垂直关系，同时可以考查学生的计算能力，是高考命题的热点，求二面角的方法通常有两个思路：一是利用空间向量，建立坐标系，这种方法优点是思路清晰、方法明确，但是计算量较大；二是传统方法，求出二面角平面角的大小，这种解法的关键是找到平面角.‎ ‎18．将一副斜边长相等的直角三角板拼接成如图所示的空间图形，其中，.若将它们的斜边重合，让三角形以为轴转动，则下列说法不正确的是（ ）‎ A． 当平面平面时，，两点间的距离为 B． 当平面平面时，与平面所成的角为 C． 在三角形转动过程中，总有 D． 在三角形转动过程中，三棱锥的体积最大可达到 ‎【答案】C ‎【解析】分析：A选项，结合图象，利用面面垂直的性质及直角三角形斜边上的中线长等于斜边长的一半求解；B选项，先作出与平面所成的角，再求得其为；C选项用反证法，假设垂直，根据线面垂直的判定与性质推到是否可能，从而得出结论；D选项根据棱锥的体积公式，在底面积不变的情况下，体积的大小取决于高，当平面ABD⊥平面ABC时，高最大，求出即可．‎ 详解：A选项，取AB中点O，连接DO、CO，‎ ‎∵AD=BD=，∴DO=1，AB=2，OC=1‎ ‎∵平面ABD⊥平面ABC，DO⊥AB，∴DO⊥平面ABC，DO⊥OC，‎ ‎∴DC=，A选项正确；‎ B选项，过点D作DM⊥AB，连接MC，则∠DCM就是与平面所成的角，因为DM=CM,所以∠DCM=45°，所以B选项正确；‎ C选项，若AB⊥CD，则AB⊥平面CDO，AB⊥OC，∵O为中点，∴AC=BC，∠BAC=45°与∠BAC=30°矛盾，∴C选项错误；‎ D选项，当DO⊥平面ABC时，棱锥的高最大，此时V棱锥=×AC×BC×DO=××1×1=．D选项正确．‎ 故答案为：C 点睛：（1）本题主要考查空间线面位置关系和空间角的计算，意在考查学生对这些知识的掌握水平和空间想象能力.(2)解答类似空间真假命题的判断，方法比较灵活，有的可以举反例，有的可以反证，有的可以直接证明.‎ ‎19．已知正方体的棱长为2，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为 A． B． C． D． ‎ ‎【答案】A ‎【解析】分析：利用正方体棱的关系，判断平面α所成的角都相等的位置，然后求解α截此正方体所得截面面积的最大值．‎ 点睛：本题考查直线与平面所成角的大小关系，考查空间想象能力以及计算能力，属于难题．解题关键是平面α与平面A平行.‎ ‎20．在三棱柱中，各棱长相等，侧棱垂直于底面，点D是侧面的中心，则AD与平面所成角的大小是( )‎ A． 30° B． 45° C． 60° D． 90°‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 三棱柱是正三棱柱，取的中点，则就是与平面所成角，解直角三角形求出的大小，即为所求．‎ ‎【详解】‎ 由题意可得，三棱柱是正三棱柱， 取的中点，则， 就是在平面内的射影，故就是与平面 所成角， 设三棱柱的棱长为1，直角三角形中， ‎ ‎， 故选C．‎ ‎【点睛】‎ 本题考查直线与平面成的角的定义和求法，取BC的中点E，判断∠ADE就是AD与平面BB1C1C所成角，是解题的关键，属于中档题 二、填空题 ‎21．在三棱锥中，与共斜边，且与平面所成角正弦值为，，，则到平面的距离为________.‎ ‎【答案】或 ‎【解析】‎ ‎【分析】‎ 由题意易知，是等腰三角形，且在底面的射影在中线上，结合与平面所成角正弦值为，可知，从而可以解得到平面的距离 ‎【详解】‎ 知与全等，所以是等腰三角形，且在底面的射影在中线上，如图底面，设，则在中，与平面所成角正弦值为知，，在及中，，，，，‎ 又，解得或 故答案为：或 ‎【点睛】‎ 求点平面的距离，第一种方法是根据定义作出垂线段，然后只要通过解三角形求出这个线段的长即可，要注意这里有三个步骤：一作二证三算；第二种方法利用体积法计算，所求距离作为一个三棱锥的高，通过两种不同的方法求三棱锥的体积，然后求得这个高；第三咱方法是利用空间向量法，点到平面的距离就是此点到平面的任一斜线段在平面的法向量方向上的投影的绝对值. ‎ ‎22．如图，正四棱锥的体积为2，底面积为6，为侧棱的中点，则直线与平面所成的角为_______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 首先找到线面角，然后利用三角函数计算角的大小即可.‎ ‎【详解】‎ ‎【点睛】‎ 本题主要考查锥体的空间结构，线面角的计算等知识，意在考查学生的转化能力和计算求解能力.‎ ‎23．已知三棱锥的三条侧棱两两互相垂直，且，，则点到平面的距离为______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据题意，利用等体积法，计算P点到平面ABC的距离，只需求出△ABC的面积 ‎【详解】‎ ‎∵PA、PB、PC两两互相垂直，且PA= ，PB=PC= ‎ ‎∴AB=AC= 5，BC=6‎ ‎∴A到BC的距离为4∴△ABC的面积为 ‎ 设P点到平面ABC的距离为h，则，解得h= ‎ 即P点到平面ABC的距离为 ‎【点睛】‎ 求点到面距离的等体积法:已知或易求出三棱锥的体积，和所求面的面积，应用 即可求出，点到该面的距离。‎ ‎24．如图,三棱锥,平面平面,若,则△的形状为__________. ‎ ‎【答案】直角三角形 ‎【解析】‎ ‎【分析】‎ 根据面面垂直的性质即可得到面，根据线面垂直的性质可得到，从而可得结果.‎ ‎【详解】‎ ‎【点睛】‎ 解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.‎ ‎25．如图，正方体中，直线和所成角的大小为___________，直线和平面所成角的大小为___________．‎ ‎【答案】 ‎ ‎【解析】‎ ‎【分析】‎ 连结DC1，A1C1，设A1C1∩B1D1=O，连结BO，由B1D1∥BD，得∠DBC1是线BC1和B1D1所成角，由此能求出直线BC1和B1D1所成角的大小；推导出C1O⊥平面B1D1DB，从而∠OBC1是直线BC1和平面B1D1DB所成角，由此能求出直线BC1和平面B1D1DB所成角的大小．‎ ‎【详解】‎ 故答案为：60°，30°．‎ ‎【点睛】‎ 本题主要考查异面直线所成的角问题,难度一般．求异面直线所成角的步骤:1平移,将两条异面直线平移成相交直线．2定角,根据异面直线所成角的定义找出所成角．3求角,在三角形中用余弦定理或正弦定理或三角函数求角．4结论．‎ ‎26．如图，在直四棱柱中，当底面四边形满足条件__________时．有 ‎．（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形）‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据题意，由，结合直棱柱的性质，分析底面四边形，只要，进而验证即可．‎ ‎【详解】‎ ‎∵四棱柱是直棱柱， ‎ ‎∴，‎ 若，则平面，‎ ‎∴，‎ 又由，则有，‎ 反之，由亦可得到．‎ 即答案为..‎ ‎【点睛】‎ 题主要考查了棱柱的几何特征以及空间线线，线面，面面垂直关系的转化与应用．‎ ‎27．三棱锥P－ABC中，PA＝PB＝PC＝AB＝AC＝1，∠BAC＝90°，则直线PA与底面ABC所成角的大小为________________．‎ ‎【答案】45°‎ ‎【解析】‎ ‎【分析】‎ 先求出∠PAE＝45°，再证明∠PAE为直线PA与平面ABC所成角．即得解.‎ ‎【详解】‎ ‎【点睛】‎ ‎(1)本题主要考查直线和平面所成的角的计算，意在考察学生对该知识的掌握水平和分析推理能力.(2) 直线和平面所成的角的求法方法一：（几何法）找作（定义法）证（定义）指求（解三角形），其关键是找到直线在平面内的射影作出直线和平面所成的角和解三角形.方法二：（向量法），其中是直线的方向向量，是平面的法向量，是直线和平面所成的角.‎ ‎28．在直三棱柱中，.有下列条件：‎ ‎①；‎ ‎②；‎ ‎③.‎ 其中能成为的充要条件的是__________．（填上序号）‎ ‎【答案】①③‎ ‎【解析】分析：由题意，对所给的三个条件，结合直三棱柱中，，作出如图的图象，借助图象对的充要条件进行研究. ‎ 详解：‎ 若①，‎ 如图取分别是的中点，‎ 可得，‎ 由直三棱柱中，‎ 可得都垂直于侧面，‎ 由此知都垂直于线，又，‎ 所以平面，‎ 可得，‎ 又由是中点及直三棱柱的性质知，‎ 故可得，‎ 再结合垂直于线，可得面，‎ 故有，故①能成为的充要条件，‎ 同理③也可，‎ 对于条件②，若，可得面，‎ ‎，若，‎ 由此可得平面形，矛盾，‎ 故不为的充要条件，‎ 综上，①③符合题意，故答案为①③.‎ 点睛：本题主要考查直棱柱的性质、线面垂直的判定定理及面面垂直的性质，属于难题.解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面. ‎ ‎29．在四面体中，，，.当四面体体积最大时，直线与平面所成的角是__________．‎ ‎【答案】‎ ‎【解析】分析：当平面时，四面体的体积最大，此时直线与平面所成角就是，利用等腰直角三角形性质可得结果.‎ 详解：‎ ‎ ‎ 如图，将四面体置于棱长为的正方体中，‎ 显然当平面时，四面体的体积最大，‎ 此时直线与平面所成角就是，‎ 而，故直线与平面所成角就是，故答案为.‎ 点睛：本题主要考查直线与平面所成的角，属于中档题.求直线与平面所成的角由两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可.‎ ‎30．如图，正方体中，异面直线与所成角为__________．‎ ‎【答案】‎ ‎【解析】分析：首先确定线面垂直，据此确定异面直线所成的角即可.‎ 点睛：本题主要考查线面垂直的判断定理，异面直线夹角的计算等知识，意在考查学生的转化能力和计算求解能力.‎ ‎31．如图,在四棱锥中,底面是矩形, 平面,则四个侧面，‎ 中,有_________ 个直角三角形.‎ ‎【答案】.‎ ‎【解析】分析：由平面可得，是直角三角形，可证明平面，平面，可得，是直角三角形，从而可得结果.‎ 点睛：本题主要考查线面垂直的判定定理以及线面垂直的性质，属于中档题. 解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理. ‎ ‎32．已知正四棱锥内接于半径为的球中（且球心在该棱锥内部），底面的边长为，则点到平面的距离是__________．‎ ‎【答案】.‎ ‎【解析】分析：设点到平面的距离为，则由，利用三棱锥的体积公式，列出方程，即可求解.‎ 详解：如图所示，连接与交于，显然球心在正棱锥的高上，‎ 因为球的半径为，所以，‎ 又因为底面的边长为，所以，，‎ 在中，由勾股定理得,‎ 所以，‎ 设点到平面的距离为，则由，可得：‎ ‎，解得.‎ 点睛：本题主要考查了等积法求解点到平面的距离，其中正确把握空间几何体的结构特征，转化为等体积法求解是解答的关键，着重考查了转化与化归方法，以及考生分析问题和解答问题的能力，试题有一定的难度，属于中档试题.‎ ‎33．已知圆锥的顶点为，母线，所成角的余弦值为，与圆锥底面所成角为45°，若的面积为，则该圆锥的侧面积为__________．‎ ‎【答案】‎ ‎【解析】分析：先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式求结果.‎ 点睛：本题考查线面角，圆锥的侧面积，三角形面积等知识点，考查学生空间想象与运算能力 ‎34．如图，圆锥的底面圆直径AB为2，母线长SA为4，若小虫P从点A开始绕着圆锥表面爬行一圈到SA的中点C，则小虫爬行的最短距离为________．‎ ‎【答案】2.‎ ‎【解析】分析：要求小虫爬行的最短距离，需将圆锥的侧面展开，进而根据“两点之间线段最短”得出结果．‎ 详解：‎ 由题意知底面圆的直径AB＝2，‎ 故底面周长等于2π.‎ 设圆锥的侧面展开后的扇形圆心角为n°，‎ 根据底面周长等于展开后扇形的弧长得2π＝，‎ 解得n＝90，‎ 所以展开图中∠PSC＝90°，‎ 根据勾股定理求得PC＝2，‎ 所以小虫爬行的最短距离为2.‎ 故答案为2‎ 点睛：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决．‎ ‎35．在长方体中，，，则直线与平面所成角的正弦值为__________．‎ ‎【答案】‎ ‎【解析】分析：过作，垂足为，则平面，则即为所求平面角，从而可得结果.‎ 详解：依题意，画出图形，如图，‎ 过作，垂足为，‎ 由平面，‎ 可得，‎ 所以平面，‎ 则即为所求平面角，‎ 因为，，‎ 所以，故答案为.‎ 点睛：本题考查长方体的性质，以及直线与平面所成的角，属于中档题.求直线与平面所成的角由两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可. ‎ ‎36．过正四棱锥的顶点与四个侧面所成的锐二面角都相等的平面有__________个.‎ ‎【答案】3.‎ ‎【解析】分析：根据正四棱锥的图形逐一超出即可.‎ 详解：如图：，故过正四棱锥的顶点与四个侧面所成的锐二面角都相等的平面，根对称性可得：有面ABCD，面PAC,面PBD，故有三个面，答案为3‎ 点睛：考查正四棱锥的特点和二面角定义，熟知正四棱锥的特点是解题关键.‎ ‎37．如图，正方体中，为面（包括边界）内一动点，当点与重合时，异面直线与所成的角的大小为__________；当点在运动过程中始终保持平面，则点的轨迹是__________．‎ ‎【答案】 . 线段.‎ ‎【解析】分析：当点与重合时，即,根据线线角定义即直线与所成的角；∵平面平面，平面，且在平面内，∴点在平面与平面的交线上.‎ 点睛：考查线线角定义，计算，线面平行，对此类题对常用的定理结论要清晰，属于中档题.‎ ‎38．从正方体的个顶点中任意选择个点，记这个点确定的平面为，则垂直于直线的平面的个数为__________．‎ ‎【答案】2.‎ ‎【解析】分析：作出草图根据线面垂直的判定定理证明即可.‎ 详解：‎ 与直线垂直的平面有平面和平面，故与直线垂直的平面的个数为．‎ 点睛：考查线面垂直，对定理的熟悉是解题关键，属于基础题.‎ ‎39．如图在正三角形中，，，分别为各边的中点，，，，分别为、、、的中点，将沿、、折成三棱锥以后，与所成角的大小为__________．‎ ‎【答案】.‎ ‎【解析】分析：将△ABC沿DE，EF，DF折成三棱锥以后，I，J分别为BE、DE的中点，则IJ∥侧棱，故GH与IJ所成角与侧棱与GH所成的角相等．AD为折成三棱锥的侧棱，则GH与IJ所成角的度数为60°‎ 详解：‎ 将沿，，折成三棱锥以后，点，，重合为点，得到三棱锥，‎ ‎∵，分别为，的中点，‎ ‎∴侧棱，‎ ‎∴与所成的角即是与所成的角，‎ ‎∵，‎ ‎∴与所成角的大小为．‎ 点睛：此题主要考查异面直线的角度及余弦值计算．‎ ‎40．在长方体中，和与底面所成的角分别为和，则异面直线和所成的角的余弦值为__________．‎ ‎【答案】‎ ‎【解析】分析：设B1B=a，B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°推知BC=a，DC=‎ a推知表示出长方体从一个顶点出发的三条棱的长度推知面对角线的长度，再用余弦定理求解 点睛：本题主要考查异面直线所角的基本求法，若所成的角在直角三角形中，则用三角函数的定义，若在一般三角形中则用余弦定理．‎ 三、解答题 ‎41．如图，在直三棱柱中，是上的一点，，且.‎ ‎（1）求证：平面；‎ ‎（2）若，求点到平面的距离.‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）连接A1B交AB1于E，连接DE，根据中位线定理即可得出DE∥A1C，故而A1C∥平面AB1D1；‎ ‎（2）过B作BF⊥B1D，则可证BF⊥平面AB1D，于是点A1到平面AB1D的距离等于C到平面AB1D的距离，等于B到平面AB1D的距离BF．‎ ‎【详解】‎ ‎（1）如图，‎ 连接，交于点，再连接，‎ 据直棱柱性质知，四边形为平行四边形，为的中点，‎ ‎∵当时，，∴是的中点，∴，‎ 又平面，平面，∴平面.‎ ‎【点睛】‎ 本题考查了线面平行的判定，点面距离的计算，属于中档题．‎ ‎42．如图，在四棱锥中，底面为平行四边形，，，且底面.‎ ‎（1）证明：平面；‎ ‎（2）若为的中点，求三棱锥的体积.‎ ‎【答案】（1）见解析;（2）.‎ ‎【解析】‎ 试题分析：（1）先证明，再说明，根据底面，可得，即可证出；（2）因为三棱锥的体积与三棱锥的体积相等，可转化为求三棱锥的体积，再换顶点为Q，并利用Q是中点转化为求解即可.‎ 试题解析：‎ ‎（1）证明：∵，∴，‎ ‎∵，∴.‎ 又∵底面，∴.‎ ‎∵，∴平面.‎ ‎（2）三棱锥的体积与三棱锥的体积相等，‎ 而 .‎ 所以三棱锥的体积.‎ 点睛：涉及几何体，特别是棱锥的体积计算问题，一般要进行转化，变换顶点后，有时还需要利用等底等高转换，还可以利用直线上的点为中点或三等分点再进行顶点变换，从而求出几何体的体积.‎ ‎43．如图，在斜三棱柱中，已知，，且.‎ ‎（Ⅰ）求证：平面平面； ‎ ‎（Ⅱ）若，求四棱锥的体积.‎ ‎【答案】(1)见解析；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）连接，易证得，，所以，所以，从而可证得 ‎，即可证得结论；‎ ‎（2）由即可得解.‎ ‎【详解】‎ ‎（2）‎ ‎.‎ 故四棱锥的体积为.‎ ‎【点睛】‎ 求锥体的体积要充分利用多面体的截面和旋转体的轴截面，将空间问题转化为平面问题求解，注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法：求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决．②等积法：等积法包括等面积法和等体积法．‎ ‎44．如图，三棱柱中，，，.‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若平面平面，，求直线与平面所成角的正弦值. ‎ ‎【答案】（1）见解析； （2） .‎ ‎【解析】‎ ‎【分析】‎ ‎（Ⅰ）取AB的中点O，连接OC，OA1，A1B，由已知可证OA1⊥AB，AB⊥平面OA1C，进而可得AB⊥A1C；‎ ‎（Ⅱ）易证OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立坐标系，可得，，的坐标，设=（x，y，z）为平面BB1C1C的法向量，则，可解得=（，1，﹣1），可求|cos＜，＞|，即为所求正弦值．‎ ‎【详解】‎ ‎（Ⅱ）由（Ⅰ）知，.‎ 又平面平面，交线为，所以平面，故，，两两相互垂直.‎ 以O为坐标原点，的方向为x轴的正方向，为单位长，建立如图所示的空间直角坐标系.‎ 由题设知，，，.‎ 则，，. ‎ 设是平面的法向量，‎ 则 即 可取.‎ 故 ，‎ 所以与平面所成角的正弦值为.‎ ‎【点睛】‎ 利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.‎ ‎45．如图：直线平面，直线平行四边形，四棱锥的顶点在平面上， ，，，， ，，、分别是与的中点．‎ ‎（Ⅰ）求证：平面 ；‎ ‎（Ⅱ）求三棱锥的体积．‎ ‎【答案】（1）见解析；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先根据三角形中位线性质得 ， ，再根据线面平行判定定理以及面面平行判定定理得平面平面，最后根据面面平行性质得结论，（2）先根据线面垂直得面面垂直：平面平面，，再根据面面垂直性质定理得平面，最后根据等体积法以及锥体体积公式求结果.‎ ‎【详解】‎ ‎（Ⅱ）由平面，平行四边形 平面底面，， ，底面 ‎ 四边形为矩形， 即四边形为直角梯形，平面平面，‎ 过作交于, 平面，即平面 由，，，知 ，‎ ‎ ，得 ‎ ‎ ．‎ ‎【点睛】‎ 垂直、平行关系证明中应用转化与化归思想的常见类型.‎ ‎(1)证明线面、面面平行，需转化为证明线线平行.‎ ‎(2)证明线面垂直，需转化为证明线线垂直. ‎ ‎(3)证明线线垂直，需转化为证明线面垂直.‎ ‎46．如图，四棱锥中，，//，，为正三角形. 若，且与底面所成角的正切值为.‎ ‎（1）证明：平面平面；‎ ‎（2）是线段上一点，记（），是否存在实数，使二面角的余弦值为？若存在，求出的值；若不存在，请说明理由.‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ 证法一：先计算出，结合已知得，由勾股定理得，又，可以证得平面，平面平面 证法二：设在平面内的射影为，连接，结合已知条件得，可求得，，四边形是正方形，即可证得垂直关系 ‎，，两两垂直，以它们所在直线分别为轴，轴，轴，建立空间直角坐标系，求出平面的法向量，平面的法向量，继而求出的值 ‎【详解】‎ ‎（1）证法一：，且，，‎ 又为正三角形，所以，‎ 又，，所以，‎ 又，//，，，‎ 所以平面，又因为平面，‎ 所以平面平面.‎ 证法二： 设在平面内的射影为，连接,‎ 则即为在平面内的射影，故即为 与底面所成的角，因为,所以 而，，所以，‎ 又为正三角形，所以,所以 由，，得，所以 ，从而是正方形，‎ 由，得：平面，于是平面平面.‎ ‎【点睛】‎ 本题考查了面面垂直的判定，在立体几何中当条件给出棱长的数值，可以考虑运用勾股定理的逆定理来证明垂直，本题在求二面角时建立空间坐标系，求出法向量继而求解，一定要掌握此类题目的解答方法。‎ ‎47．如图，四棱锥中，，//，，为正三角形. 且.‎ ‎（Ⅰ）证明：平面平面；‎ ‎（Ⅱ）若点到底面的距离为2，是线段上一点，且//平面，求四面体的体积. ‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（Ⅰ）证明，，可证平面平面；‎ ‎（Ⅱ）如图，连接，交于点，因为//，由（Ⅰ）点到平面的距离为2，‎ 所以点到平面的距离为，所以由可求四面体的体积.‎ ‎【详解】‎ ‎（Ⅱ）如图，连接，交于点，因为//，‎ 且，所以，连接，‎ 因为//平面，所以//，则，‎ 由（Ⅰ）点到平面的距离为2，‎ 所以点到平面的距离为，‎ 所以，‎ 即四面体的体积为.‎ ‎【点睛】‎ 本题考查面面垂直的证明以及锥体体积的实际，属中档题.‎ ‎48．如图，四边形为等腰梯形沿折起，使得平面平面为的中点，连接（如图2）.‎ 图1 图2‎ ‎（Ⅰ）求证： ；‎ ‎（Ⅱ）求直线与平面所成的角的正弦值.‎ ‎【答案】（Ⅰ）证明见解析；（Ⅱ）.‎ ‎【解析】‎ ‎【分析】‎ ‎（I）证明，结合平面 平面，推出平面，然后证明． （II）取AC中点F，连接EF、EC E，设E点到平面BCD的距离为，，,利用则求解直线DE与平面BCD所成的角的正弦值即可．‎ ‎【详解】‎ ‎（Ⅰ）,则,，又因为平面 平面且平面 平面 ，所以平面，从而．‎ ‎【点睛】‎ 本题考查直线与平面所成角的求法，直线与平面垂直的判定定理以及性质定理的应用，考查空间想象能力以及计算能力．‎ ‎49．如图，四棱锥，，，，，M，O分别为CD和AC的中点，平面ABCD．‎ 求证：平面平面PAC；‎ Ⅱ是否存在线段PM上一点N，使得平面PAB，若存在，求的值，如果不存在，说明理由．‎ ‎【答案】（1）见解析（2）当N为PM靠近P点的三等分点时，平面PAB．‎ ‎【解析】‎ ‎【分析】‎ 连结MO并延长交AB于E，设AC，BM的交点为则，故≌，于是，，根据勾股定理求出AC，BM的值得出BF，CF，由勾股定理得逆定理得出，又由平面ABCD得，故BF平面PAC，于是平面平面PAC；‎ 连结PE，则当平面PAB时，，故当时，结论成立．‎ ‎【详解】‎ 解：连结MO并延长交AB于E，设AC，BM的交点为F．‎ ‎，O是CD，AC的中点，，，‎ 是AB的中点，．‎ ‎．‎ ‎．‎ ‎，，‎ ‎≌，‎ ‎，．‎ ‎，．‎ ‎，，即．‎ 平面ABCD，平面ABCD，‎ ‎，又平面PAC，平面PAC，，‎ 平面PAC，又平面PBM，‎ 平面．‎ ‎【点睛】‎ 本题考查了面面垂直的判定，线面平行的判定，属于中档题．‎