- 605.00 KB
- 2021-06-25 发布
2017-2018学年四川省乐山沫若中学高二下学期期中考试(文数)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、在某班的50名学生中,依次抽取学号为5、10、15、20、25、30、35、40、45、50的10名学生进行作业检查,这种抽样方法是
A.随机抽样 B.分层抽样 C.系统抽样 D.以上都不是
2、复数z满足,则
A. B. C. D.
3、把十进制数189化为三进制数,末位数是( )
A. 3 B. 2 C. 1 D. 0
4、一个陀螺模型的三视图如图所示,则其表面积是( )
A. B.
C. D.
5、从3名男生和2名女生中任意推选2名选手参加辩论赛,则推选的2名选手恰好是1男1女的概率是( )
A. B. C. D.
6、在区间上随机取两个数,则的概率是( )
A. B. C. D.
7、如图是甲、乙两名篮球运动员2015年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和是
A. 53 B. 54
C. 55 D. 56
8、我们知道:在平面内,点(x0,y0)到直线Ax+By+C=0的距离公式为d=,通过类比的方法,可求得:在空间中,点(2,4,1)到平面x+2y+3z+3=0的距离为( )
A. 3 B. 5 C. D. 3
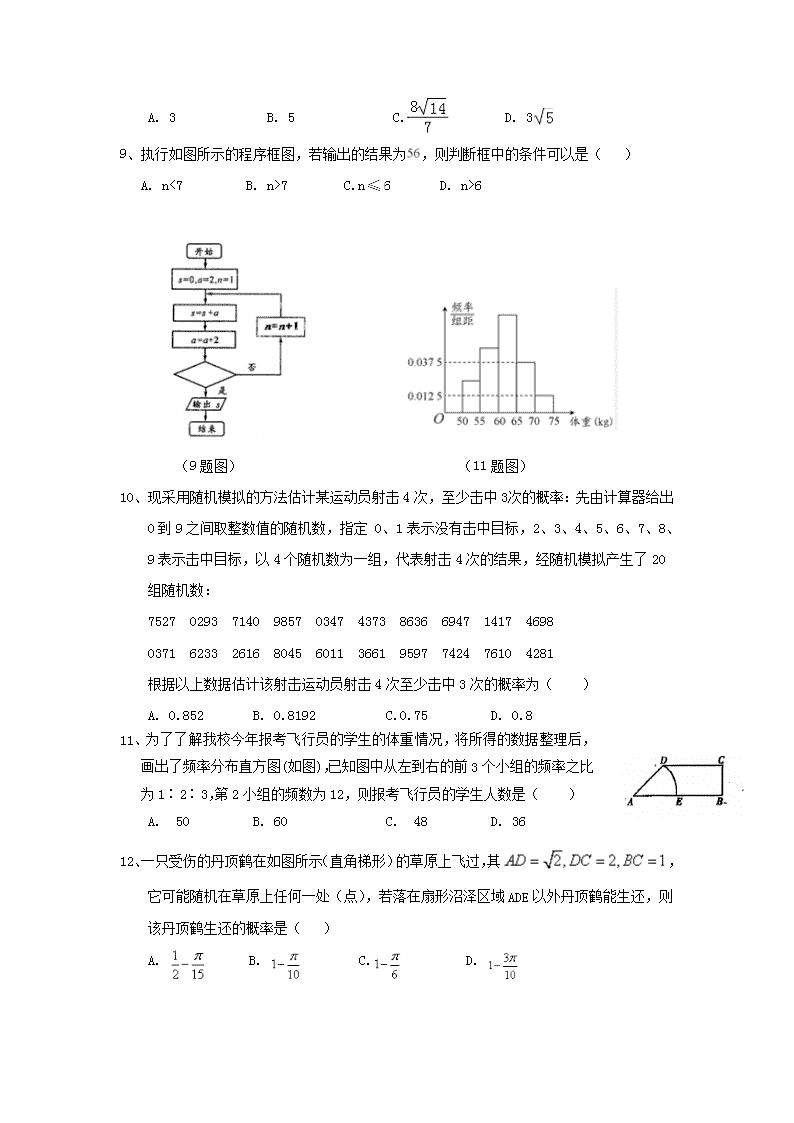
9、执行如图所示的程序框图,若输出的结果为,则判断框中的条件可以是( )
A. n<7 B. n>7 C.n6 D. n>6
(9题图) (11题图)
10、现采用随机模拟的方法估计某运动员射击4次,至少击中3 次的概率:先由计算器给出0到9之间取整数值的随机数,指定 0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A. 0.852 B. 0.8192 C.0.75 D. 0.8
11、为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,则报考飞行员的学生人数是( )
A. 50 B. 60 C. 48 D. 36
12、一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过,其,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是( )
A. B. C. D.
二、填空题
13、已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为y=bx+a必过点 .
14、甲乙丙三人代表班级参加校运会的跑步,跳远,铅球比赛,每人参加一项,每项都要有人参加,他们的身高各不同,现了解到已下情况:
(1)甲不是最高的;(2)最高的是没报铅球;(3)最矮的参加了跳远;(4)乙不是最矮的,也没参加跑步.
可以判断丙参加的比赛项目是 .
15、已知程序框图,则输出的i= .
16、正方体ABCD-EFGH的棱长为1,在正方体内随机取一点,使得四棱锥M-ABCD的体积小于的概率为 .
三、计算题
17、已知l﹣2i是关于x的方程x2+a=bx的一个根.
(1)求a,b的值;
(2)同时掷两个骰子,记它们向上的点数分别为m、n,求复数(m﹣a)+(n﹣b)i在复平面内对应的点位于第二象限的概率。
18、2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段
人数(单位:人)
180
180
160
80
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列列联表,并回答能否有的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事
不热衷关心民生大事
总计
青年
12
中年
5
总计
30
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
19、某高中有高一新生500名,分成水平相同的A,B两类进行教学实验.为对比教学效果,现用分层抽样的方法从A、B两类学生中分别抽取了40人、60人进行测试.
(Ⅰ)求该学校高一新生A、B两类学生各多少人?
(Ⅱ)经过测试,得到以下三个数据图表:
图一:75分以上A、B两类参加测试学生成绩的茎叶图
A类
B类
7,6,5,5
7
5,6,7,7,8,9
3,1
8
1,3,4
(茎、叶分别是十位和个位上的数字)(如图)
表一:100名测试学生成绩频率分布表;图二:100名测试学生成绩的频率分布直方图;
①先填写频率分布表(表一)中的六个空格,然后将频率分布直方图(图二)补充完整;
②该学校拟定从参加考试的79分以上(含79分)的B类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
20、某地区某农产品近几年的产量统计如下表:
年 份
2012
2013
2014
2015
2016
2017
年份代码t
1
2
3
4
5
6
年产量y(万吨)
6.6
6.7
7
7.1
7.2
7.4
(1)根据表中数据,建立关于的线性回归方程;
(2)根据(1)中所建立的回归方程预测该地区2018年()该农产品的产量.
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:,.
21、某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率.
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
22 、如图,四棱锥中,平面,为线段上一点,,为的中点.
(1)证明:
(2)求四面体的体积.
高二下期半期考试答案(文)
一选择题
C A D D C A B C D C C B
二填空题
13 (1.5, 4 ) 14 跑步 15 7 16 0.5
三计算题
17解:(1)将l﹣2i代入x的方程x2+a=bx,易求出,解得a=5,b=2.
(2)同时掷两个骰子,记它们向上的点数分别为m、n,基本事件(m,n)的总数N=6×6=36,列举略∵复数(m﹣a)+(n﹣b)i即复数(m﹣5)+(n﹣2)i在复平面内对应的点位于第二象限,∴,即,
∴复数(m﹣a)+(n﹣b)i在复平面内对应的点位于第二象限包含的基本事件(m,n)有:
(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6),(4,3),(4,4),(4,5),(4,6),共16个,
∴复数(m﹣a)+(n﹣b)i在复平面内对应的点位于第二象限的概率p=.
18(1)抽出的青年观众为18人,中年观众12人
(2)二联表略。K=1.833所以∴没有的把握认为年龄层与热衷关心民生大事有关.
(3)热衷关心民生大事的青年观众有6人,记能胜任才艺表演的四人为,其余两人记为,则从中选两人,一共有如下15种情况:
抽出的2人都能胜任才艺表演的有6种情况,所以.
19(Ⅰ)由题知A类学生有则B类学生有(
Ⅱ)填图略②79分以上的B类学生共4人,记80分以上的三人分别是{1,2,3},79分的学生为{a}.从中抽取2人,有:12,13,1a,23,2a,3a
,共6种抽法;抽出的2人均在80分以上有::12,13,23,共3种抽法.则抽到2人均在80分以上的概率为.
20(1)由题,,,
.所以,又,得,
所以y关于t的线性回归方程为.
(2)由(1)知, 当时,,
即该地区2018年该农产品的产量估计值为7.56万吨.
21解:(1)由题意可得,∴n=160;
(2)高二代表队6人,从中抽取2人上台抽奖的基本事件有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b.f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种,其中a和b至少有一人上台抽奖的基本事件有9种,
∴a和b至少有一人上台抽奖的概率为=;
(3)由已知0≤x≤1,0≤y≤1,点(x,y)在如图所示的正方形OABC内,
由条件得到的区域为图中的阴影部分
由2x﹣y﹣1=0,令y=0可得x=,令y=1可得x=1
∴在x,y∈[0,1]时满足2x﹣y﹣1≤0的区域的面积为=
∴该代表中奖的概率为=.
22:(1)由已知得,取的中点,连接,由为中点知,即又,即故四边形为平行四边形,于是因为所以