- 1.17 MB
- 2021-06-25 发布
2017-2018学年河北省邢台市高二上学期第一次月考数学理试题
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
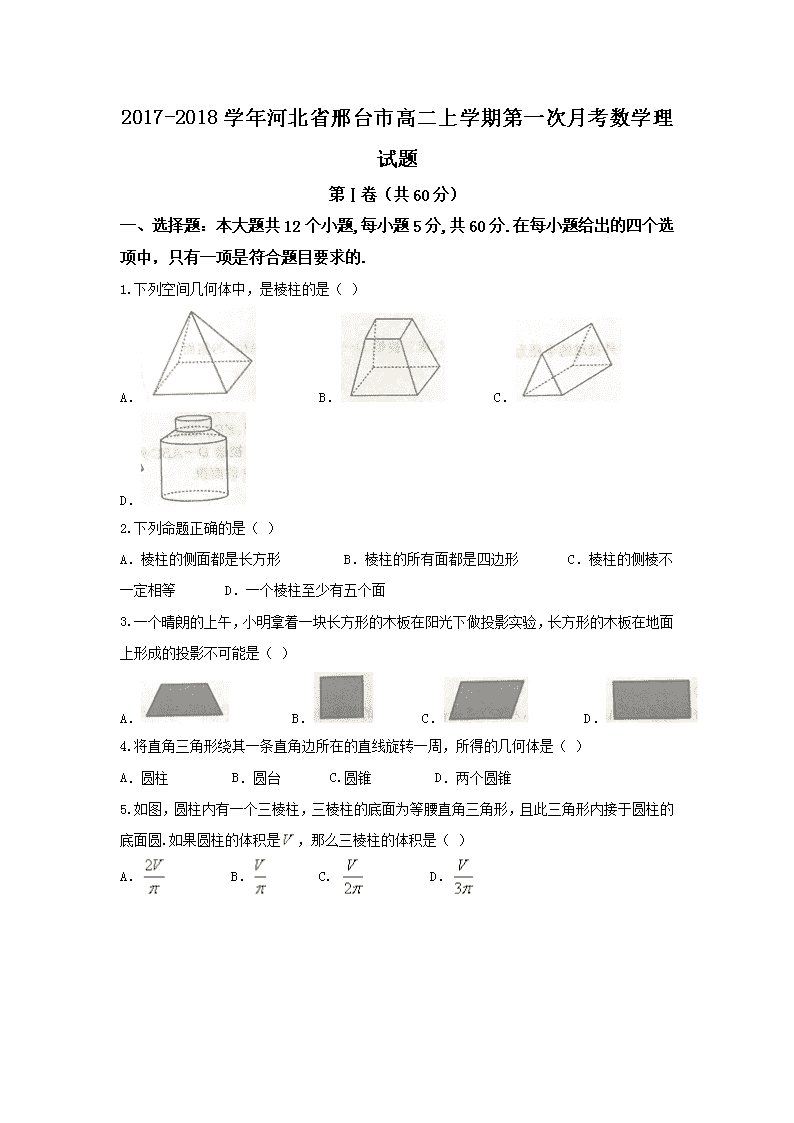
1.下列空间几何体中,是棱柱的是( )
A. B. C. D.
2.下列命题正确的是( )
A.棱柱的侧面都是长方形 B.棱柱的所有面都是四边形 C.棱柱的侧棱不一定相等 D.一个棱柱至少有五个面
3.一个晴朗的上午,小明拿着一块长方形的木板在阳光下做投影实验,长方形的木板在地面上形成的投影不可能是( )
A. B. C. D.
4.将直角三角形绕其一条直角边所在的直线旋转一周,所得的几何体是( )
A.圆柱 B.圆台 C.圆锥 D.两个圆锥
5.如图,圆柱内有一个三棱柱,三棱柱的底面为等腰直角三角形,且此三角形内接于圆柱的底面圆.如果圆柱的体积是,那么三棱柱的体积是( )
A. B. C. D.
6.下列四个命题:
①若两个平面垂直于同一条直线,则这两个平面平行;
②若直线与平面内的无数条直线垂直,则;
③若一个平面内的三个不等式的点到另一个平面的距离都相等,则这两个平面平行;
④如直线不垂直于平面,则平面内没有与直线垂直的直线.
其中正确的命题的个数是( )
A. B. C. D.
7.圆台的上、下两个底面圆的半径分别为和,母线与底面的夹角是,则圆台的母线长( )
A. B. C. D.
8.在长方体的十二条棱中,与面对角线垂直且异面的棱的条数是( )
A. B. C. D.
9.已知两条不同的直线和平面,下列结论正确的是( )
①,则;
②,则;
③,则
④与平面所成角的大小等于与平面所成角的大小,则.
A.①③ B.①② C. ②③ D.①④
10.在平面四边形中,,将沿对角线所在的直线折起,使平面平面,则直线与平面所成角为( )
A. B. C. D.
11.
一个几何体由一些完全相同的小正方体搭建而成,它的正视图与侧视图如图所示,那么搭成这个几何体所用的小正方体的个数最少为( )
A. B. C. D.
12.已知一个平行四边形的直观图是一个边长为的正方形,则此平行四边形的面积为( )
A. B. C. D.
13.将半径为的半圆围成一个圆锥,则该圆锥的内切球的表面积为( )
A. B. C. D.
14.在空间四边形中,分别是的中点,若异面直线与所成角为,则( )
A. B. C. D.
15.某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
16.如图,在长方体中,为线段上的动点,且为线段上的动点,且为棱上的动点,则下列判断正确的是( )
A.三棱锥的体积是定值,等于 B.三棱锥的体积不是定值,最小为 C.四棱锥的体积是定值,等于 D.四棱锥的体积不是定值,最大为
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
17.一个几何体的表面展开平面图如图,该几何体中的与“数”字面相对的是“ ”字面.
18.《九章算术》卷《商功》记载一个问题“今有圆堡壔(),周四丈八尺,高一丈一尺.问积几何?”意思是:今有圆柱形土筑小城堡,底面周长为丈尺,高丈尺,则它的体积是 立方尺.(取,丈尺)
19.若正四棱柱的底面边长为与底面所成的角为,则三棱锥的表面积为 .
20.一个正三棱柱的侧棱长的底面边长的倍,它的三视图中的俯视图如下图所示,侧(左)视图是一个矩形,若这个矩形的面积等于,则该正棱柱的侧面积为 .
21.如图,在四棱锥中,四个侧面都是顶角为的等腰三角形,侧棱长均为分别是上的点,则四边形周长的最小值为 .
22.一个四棱锥的三视图和直观图如图所示,其中分别是的中点,是上的一点,平面,则三棱锥的体积为 .
23.已知平面外两点到平面的距离分别为和在平面内的射影之间的距离为,则线段的长度为 .
24.在四面体中,底面为的重心,为线段上一点,且平面,则直线与所成角的余弦值为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
25. 如图,在四棱锥中,,且为的中点.
证明:平面.
26. 如图,在三棱锥中,平面为的中点,.
(1)证明:;
(2)若三棱锥外接球的半径为,求三棱锥的侧面的面积.
27.如图,在四棱锥中,是边长为的棱形,且分别是的中点.
(1)证明:平面;
(2)若二面角的大小为,求点到平面的距离.
试卷答案
一、选择题
1-5:CDACB 6-10:ADAAB 11-15:CBBCA 16:D
二、填空题
17.学 18. 19. 20. 21. 22. 23. 或 24.
三、解答题
25.证明:取的中点,连结,所以,且,
由已知,且,所以,
所以为平行四边形,即.
.
26.(1)证明:因为,所以.
因为为中点,,所以.
又,所以.
于是,故.
因为平面平面,所以.
因为,所以平面,所以.
(2)解:记三棱锥外接球球心为,则;
记的外心为,则.
如图,四边形为直角梯形,易求出.
为等腰三角形,,
故侧面的面积.
27.(1)证明:取中点,连接.
在中,,所以为正三角形.
又为中点,.
因为,所以.
又,故平面.
因为分别是的中点,所以.
又,所以平面平面
又,故平面.
(2)解:因为平面,所以,
则为二面角的平面角,即.
因为,所以.
因为,且,所以.
所以,且.
因为平面,所以.
所以平面,所以三棱锥的高为.
于是三棱锥的体积.
在中,,所以.
则在中,.
所以,于是的面积.
设点到平面的距离为,三棱锥的体积与三棱锥的体积相等.
所以,故.