- 436.50 KB
- 2021-06-24 发布
全*品*高*考*网, 用后离不了!2016-2017学年福建省福州市福清三中高二(上)期末数学模拟试卷(文科)
一、选择题(本大题共12小题,每小题5分,共60分.每小题有且只有一项是符合题目要求的.)
1.椭圆x2+=1的焦点在x轴上,长轴长是短轴长的两倍,则m的值为( )
A. B. C.2 D.4
2.双曲线方程为=1,则渐近线方程为( )
A.y=±x B.y=±2x C.y=±x D.y=x
3.双曲线﹣=1的焦距是( )
A.8 B.4 C.2 D.2
4.设f(x)=xlnx,若f′(x0)=2,则x0=( )
A.e2 B.e C. D.ln2
5.若函数f(x)=x3﹣x2+1,则( )
A.最大值为1,最小值为 B.最大值为1,无最小值
C.最小值为,无最大值 D.既无最大值也无最小值
6.过椭圆+=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
A. B. C. D.
7.函数y=(3﹣x2)ex的单调递增区间是( )
A.(﹣∞,0) B.(0,+∞) C.(﹣∞,﹣3)和(1,+∞) D.(﹣3,1)
8.设a∈R,若函数y=ex+ax,x∈R,有大于零的极值点,则( )
A.a<﹣1 B.a>﹣1 C. D.
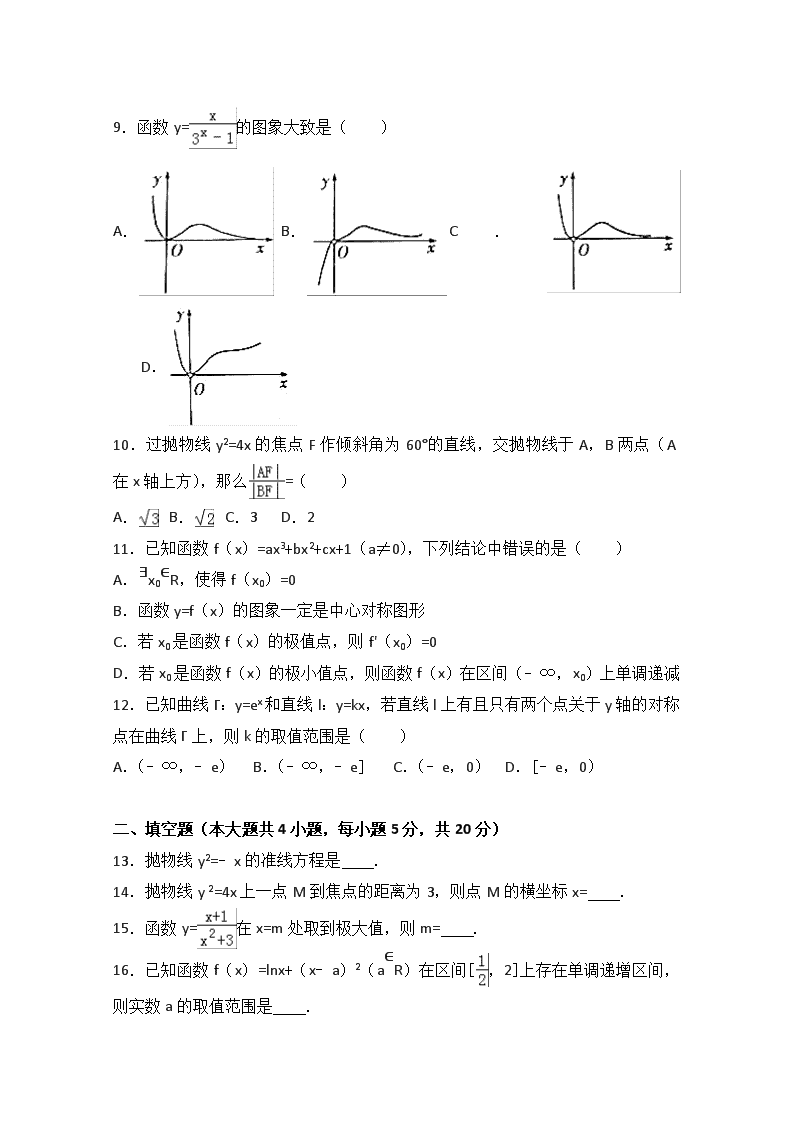
9.函数y=的图象大致是( )
A. B. C. D.
10.过抛物线y2=4x的焦点F作倾斜角为60°的直线,交抛物线于A,B两点(A在x轴上方),那么=( )
A. B. C.3 D.2
11.已知函数f(x)=ax3+bx2+cx+1(a≠0),下列结论中错误的是( )
A.∃x0∈R,使得f(x0)=0
B.函数y=f(x)的图象一定是中心对称图形
C.若x0是函数f(x)的极值点,则f'(x0)=0
D.若x0是函数f(x)的极小值点,则函数f(x)在区间(﹣∞,x0)上单调递减
12.已知曲线Γ:y=ex和直线l:y=kx,若直线l上有且只有两个点关于y轴的对称点在曲线Γ上,则k的取值范围是( )
A.(﹣∞,﹣e) B.(﹣∞,﹣e] C.(﹣e,0) D.[﹣e,0)
二、填空题(本大题共4小题,每小题5分,共20分)
13.抛物线y2=﹣x的准线方程是 .
14.抛物线y 2=4x上一点M到焦点的距离为3,则点M的横坐标x= .
15.函数y=在x=m处取到极大值,则m= .
16.已知函数f(x)=lnx+(x﹣a)2(a∈R)在区间[,2]上存在单调递增区间,则实数a的取值范围是 .
三、解答题:本大题共6小题,17题10分,其它每题12分,共70分.解答应写出文字说明,证明过程或演算步骤.
17.已知抛物线y=x2在点A(1,1)处的切线为l.
(1)求切线l的方程;
(2)若切线l经过椭圆+=1(a>b>0)的一个焦点和顶点,求该椭圆的方程.
18.设函数f(x)=2x3﹣12x+c的图象经过原点.
(1)求c的值及函数f(x)的单调区间;
(2)求函数f(x)在[﹣1,3]上的最大值和最小值.
19.在对人们休闲方式的一次调查中,仅就看电视与运动这两种休闲方式比较喜欢哪一种进行了调查. 调查结果:接受调查总人数110人,其中男、女各55人;受调查者中,女性有30人比较喜欢看电视,男性有35人比较喜欢运动.
(Ⅰ)请根据题目所提供的调查结果填写下列2×2列联表;
看电视
运动
合计
女
男
合计
(Ⅱ)已知P(K2≥3.841)=0.05.能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”?
(注:K2=,(其中n=a+b+c+d为样本容量))
20.已知椭圆G: +=1(a>b>0)的焦点和一个顶点在圆x2+y2=4上.
(1)求椭圆的方程;
(2)已知点P(﹣3,2),若斜率为1的直线l与椭圆G相交于A、B两点,试探讨以AB为底边的等腰三角形ABP是否存在?若存在,求出直线l的方程,若不存在,说明理由.
21.已知函数f(x)=ex﹣ax+1,其中a为实常数,e=2.71828…为自然对数的底数.
(1)当a=e时,求函数f(x)的单调区间;
(2)若函数f(x)在定义域内单调递增,求a的取值范围;
(3)已知a>0,并设函数f(x)的最小值为g(a),求证:g(a)≤2.
22.已知函数f(x)=lnx+ax2,其中a为实常数.
(1)讨论函数f(x)的极值点个数;
(2)若函数f(x)有两个零点,求a的取值范围.
2016-2017学年福建省福州市福清三中高二(上)期末数学模拟试卷(文科)
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分.每小题有且只有一项是符合题目要求的.)
1.椭圆x2+=1的焦点在x轴上,长轴长是短轴长的两倍,则m的值为( )
A. B. C.2 D.4
【考点】椭圆的简单性质.
【分析】由题意可得a2=1,b2=m,求出a,b的值,结合长轴长是短轴长的两倍列式求得m值.
【解答】解:∵椭圆的焦点在x轴上,
∴a2=1,b2=m,则a=1,b=,
又长轴长是短轴长的两倍,
∴2=,即m=.
故选:A.
2.双曲线方程为=1,则渐近线方程为( )
A.y=±x B.y=±2x C.y=±x D.y=x
【考点】双曲线的简单性质.
【分析】把双曲线的标准方程中的1换成0即得渐近线方程,化简即可得到所求.
【解答】解:∵双曲线方程为,则渐近线方程为,即,
故选 A.
3.双曲线﹣=1的焦距是( )
A.8 B.4 C.2 D.2
【考点】双曲线的简单性质.
【分析】利用双曲线﹣=1,求出c,即可求出双曲线﹣=1的焦距.
【解答】解:双曲线﹣=1中a=2,b=2,
∴c=4,
∴焦距是2c=8.
故选:A.
4.设f(x)=xlnx,若f′(x0)=2,则x0=( )
A.e2 B.e C. D.ln2
【考点】导数的乘法与除法法则.
【分析】利用乘积的运算法则求出函数的导数,求出f'(x0)=2解方程即可.
【解答】解:∵f(x)=xlnx
∴
∵f′(x0)=2
∴lnx0+1=2
∴x0=e,
故选B.
5.若函数f(x)=x3﹣x2+1,则( )
A.最大值为1,最小值为 B.最大值为1,无最小值
C.最小值为,无最大值 D.既无最大值也无最小值
【考点】函数的最值及其几何意义.
【分析】求函数的导数,利用导数研究函数的极值和最值,即可得到结论.
【解答】解:∵f(x)=x3﹣x2+1,
∴f′(x)=3x2﹣3x=3x(x﹣1),
则由f′(x)=3x(x﹣1)>0,解得x>1或x<0,此时函数单调递增,
由f′(x)=3x(x﹣1)<0,解得0<x<1,此时函数单调递减,
即函数在x=0处取得极大值,在x=1处取得极小值,无最大值和最小值.
故选:D.
6.过椭圆+=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
A. B. C. D.
【考点】椭圆的简单性质.
【分析】把x=﹣c代入椭圆方程求得P的坐标,进而根据∠F1PF2=60°推断出=整理得e2+2e﹣=0,进而求得椭圆的离心率e.
【解答】解:由题意知点P的坐标为(﹣c,)或(﹣c,﹣),
∵∠F1PF2=60°,
∴=,
即2ac=b2=(a2﹣c2).
∴e2+2e﹣=0,
∴e=或e=﹣(舍去).
故选B.
7.函数y=(3﹣x2)ex的单调递增区间是( )
A.(﹣∞,0) B.(0,+∞) C.(﹣∞,﹣3)和(1,+∞) D.(﹣3,1)
【考点】利用导数研究函数的单调性.
【分析】求导函数,令其大于0,解不等式,即可得到函数的单调递增区间.
【解答】解:求导函数得:y′=(﹣x2﹣2x+3)ex
令y′=(﹣x2﹣2x+3)ex>0,可得x2+2x﹣3<0
∴﹣3<x<1
∴函数y=(3﹣x2)ex的单调递增区间是(﹣3,1)
故选D.
8.设a∈R,若函数y=ex+ax,x∈R,有大于零的极值点,则( )
A.a<﹣1 B.a>﹣1 C. D.
【考点】利用导数研究函数的极值.
【分析】先对函数进行求导令导函数等于0,原函数有大于0的极值故导函数等于0有大于0的根,然后转化为两个函数观察交点,确定a的范围.
【解答】解:∵y=ex+ax,
∴y'=ex+a.
由题意知ex+a=0有大于0的实根,令y1=ex,y2=﹣a,则两曲线交点在第一象限,
结合图象易得﹣a>1⇒a<﹣1,
故选A.
9.函数y=的图象大致是( )
A. B. C. D.
【考点】函数的图象.
【分析】根据函数的变化趋势即可判断答案.
【解答】解:当x→﹣∞时,3x﹣1→﹣1,故f(x)→+∞,
当x→+∞时,3x﹣1→+∞,故f(x)→0,
又因为函数的定义域为x≠0,
综上可以判断C正确,
故选:C.
10.过抛物线y2=4x的焦点F作倾斜角为60°的直线,交抛物线于A,B两点(A在x轴上方),那么=( )
A. B. C.3 D.2
【考点】抛物线的简单性质.
【分析】设出A、B坐标,利用抛物线焦半径公式求出|AB|,结合抛物线的性质,求出A、B的坐标,然后求比值即可.
【解答】解:设A(x1,y1),B(x2,y2),则抛物线y2=4x中p=2.
|AB|=x1+x2+p==
∴x1+x2=,
又x1x2==1,可得x1=3,x2=,
则==3,
故选:C.
11.已知函数f(x)=ax3+bx2+cx+1(a≠0),下列结论中错误的是( )
A.∃x0∈R,使得f(x0)=0
B.函数y=f(x)的图象一定是中心对称图形
C.若x0是函数f(x)的极值点,则f'(x0)=0
D.若x0是函数f(x)的极小值点,则函数f(x)在区间(﹣∞,x0)上单调递减
【考点】利用导数研究函数的极值.
【分析】A.不妨设a>0,则x→﹣∞时,f(x)→﹣∞;x→+∞时,f(x)→+∞,即可判断出结论.
B.f′(x)=3ax2+2bx+c,f″(x)=6ax+2b,由于f″(x)=6a×(﹣)+2b=0,可得函数f(x)关于点对称,即可判断出结论.
C.利用函数极值点的必要条件即可判断出结论.
D.若a>0,f′(x)=3ax2+2bx+c,则二次函数y=3ax2+2bx+c的图象开口向上.若x1,x0是函数f(x)的极值点,且x0是函数f(x)的极小值点,则x1<x0,利用导数即可判断出其单调区间.
【解答】解:A.不妨设a>0,则x→﹣∞时,f(x)→﹣∞;x→+∞时,f(x)→+∞,因此函数∃x0∈R,使得f(x0)=0,正确.
B.∵f(x)=ax3+bx2+cx+1(a≠0),∴f′(x)=3ax2+2bx+c,f″(x)=6ax+2b,∵f″(x)=6a×(﹣)+2b=0,∴函数f(x)关于点对称,正确.
C.若x0是函数f(x)的极值点,则f'(x0)=0,正确.
D.若a>0,f′(x)=3ax2+2bx+c,则二次函数y=3ax2+2bx+c的图象开口向上.
若x1,x0是函数f(x)的极值点,且x0是函数f(x)的极小值点,则x1<x0,因此函数f(x)的单调递减区间为(x1,x0),单调递增区间为:(﹣∞,x1),(x0,+∞),因此不正确.
综上可知:只有D错误.
故选:D.
12.已知曲线Γ:y=ex和直线l:y=kx,若直线l上有且只有两个点关于y轴的对称点在曲线Γ上,则k的取值范围是( )
A.(﹣∞,﹣e) B.(﹣∞,﹣e] C.(﹣e,0) D.[﹣e,0)
【考点】利用导数研究曲线上某点切线方程.
【分析】求出l关于y轴的对称直线方程,把直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,转化为直线y=﹣kx与y=ex有两个交点,然后求出过原点与曲线Γ:y=ex相切的直线的斜率得答案.
【解答】解:直线l:y=kx关于y轴的对称直线方程为y=﹣kx,
要使直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,
则直线y=﹣kx与y=ex有两个交点,
如图,设过原点的直线切曲线y=ex于P(),
由y=ex,得y′=ex,∴,
则切线方程为y﹣=(x﹣x0),
把O(0,0)代入,可得x0=1,
∴切线的斜率k=e1=e,
∴﹣k>e,则k<﹣e.
∴k的取值范围是(﹣∞,﹣e).
故选:A.
二、填空题(本大题共4小题,每小题5分,共20分)
13.抛物线y2=﹣x的准线方程是 .
【考点】抛物线的简单性质.
【分析】抛物线y2=﹣x,焦点在x轴上,开口向左,2p=1,由此可得抛物线的准线方程.
【解答】解:抛物线y2=﹣x,焦点在x轴上,开口向左,2p=1,∴=
∴抛物线y2=﹣x的准线方程是
故答案为:
14.抛物线y 2=4x上一点M到焦点的距离为3,则点M的横坐标x= 2 .
【考点】抛物线的简单性质.
【分析】由抛物线的方程求出,再由已知结合抛物线定义求得点M的横坐标.
【解答】解:由抛物线y 2=4x,得2p=4,p=2,∴.
∵M在抛物线y 2=4x上,且|MF|=3,
∴xM+1=3,即xM=2.
故答案为:2.
15.函数y=在x=m处取到极大值,则m= 1 .
【考点】利用导数研究函数的极值.
【分析】求导数便得到,从而可判断导数符号,根据符号即可得出该函数的极大值点,从而得出m的值.
【解答】解: =;
∴x<﹣3时,y′<0,﹣3<x<1时,y′>0,x>1时,y′<0;
∴x=1时,原函数取得极大值;
∴m=1.
故答案为:1.
16.已知函数f(x)=lnx+(x﹣a)2(a∈R)在区间[,2]上存在单调递增区间,则实数a的取值范围是 (﹣∞,) .
【考点】利用导数研究函数的单调性.
【分析】利用导函数得到不等式恒成立,然后求解a的范围.
【解答】解:∵函数f(x)在区间[,2]上存在单调增区间,
∴函数f(x)在区间[,2]上存在子区间使得不等式f′(x)>0成立.
f′(x)=+2(x﹣a)]=,
设h(x)=2x2﹣2ax+1,则h(2)>0或h()>0,
即8﹣4a+1>0或﹣a+1>0,
得a<
故答案为:(﹣∞,).
三、解答题:本大题共6小题,17题10分,其它每题12分,共70分.解答应写出文字说明,证明过程或演算步骤.
17.已知抛物线y=x2在点A(1,1)处的切线为l.
(1)求切线l的方程;
(2)若切线l经过椭圆+=1(a>b>0)的一个焦点和顶点,求该椭圆的方程.
【考点】椭圆的简单性质;抛物线的简单性质.
【分析】(1)求导,由抛物线在点A(1,1)处的切线为l的斜率k=k切=y'|x=1=2,由点斜式方程即可求得切线l的方程;
(2)由题意可知求得切线与x和y的轴的焦点,求得c和b的值,由椭圆的性质可知a2=b2+c2,即可求得该椭圆的方程.
【解答】解:(1)k切=y'|x=1=2x|x=1=2,…
切点A(1,1),所以切线l的方程为y﹣1=2(x﹣1)
即y=2x﹣1…
(2)令y=0,则x=,所以切线与x轴的交点为…
令x=0,则y=﹣1,所以切线与y轴的交点为C(0,﹣1)
所以,
所求椭圆方程为.
18.设函数f(x)=2x3﹣12x+c的图象经过原点.
(1)求c的值及函数f(x)的单调区间;
(2)求函数f(x)在[﹣1,3]上的最大值和最小值.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
【分析】(1)由f(0)=0,求出c的值,求出函数的导数,解关于导函数的方程,求出函数的单调区间即可;(2)根据函数的单调性求出函数的最值即可.
【解答】解:(1)∵f(0)=0∴c=0…(2),
∴f(x)=2x3﹣12x…
∴,…
列表如下:
x
f'(x)
+
0
﹣
0
+
f(x)
↗
极大
↘
极小
↗
所以函数f(x)的单调增区间是和…
递减区间是…
(2)∵f(﹣1)=10,,f(3)=18
∴f(x)在[﹣1,3]上的最大值是f(3)=18,最小值是…
19.在对人们休闲方式的一次调查中,仅就看电视与运动这两种休闲方式比较喜欢哪一种进行了调查. 调查结果:接受调查总人数110人,其中男、女各55人;受调查者中,女性有30人比较喜欢看电视,男性有35人比较喜欢运动.
(Ⅰ)请根据题目所提供的调查结果填写下列2×2列联表;
看电视
运动
合计
女
男
合计
(Ⅱ)已知P(K2≥3.841)=0.05.能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”?
(注:K2=,(其中n=a+b+c+d为样本容量))
【考点】独立性检验.
【分析】(I)由题意填写列联表即可;
(II)代入数据计算K2的观测值,比较观测值与3.841的大小,判断能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”.
【解答】解:(Ⅰ)根据题目所提供的调查结果,可得下列2×2列联表:
看电视
运动
合计
女
30
25
55
男
20
35
55
合计
50
60
110
(Ⅱ)根据列联表中的数据,可计算K2的观测值k:,
∵k=3.67<k0=3.841,
∵不能在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”.
20.已知椭圆G: +=1(a>b>0)的焦点和一个顶点在圆x2+y2=4上.
(1)求椭圆的方程;
(2)已知点P(﹣3,2),若斜率为1的直线l与椭圆G相交于A、B两点,试探讨以AB为底边的等腰三角形ABP是否存在?若存在,求出直线l的方程,若不存在,说明理由.
【考点】椭圆的简单性质.
【分析】(Ⅰ)设椭圆G的右焦点为F(c,0),由题意可得:b=c,且b2+c2=8,由此能求出椭圆G的方程.
(Ⅱ)以AB为底的等腰三角形ABP存在.设斜率为1的直线l的方程为y=x+m,代入中,得:3x2+4mx+2m2﹣8=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的方程.
【解答】解:(Ⅰ)设椭圆G的右焦点为F(c,0),
由题意可得:b=c,且b2+c2=8,∴b2=c2=4,
故a2=b2+c2=8,
∴椭圆G的方程为
(Ⅱ)以AB为底的等腰三角形ABP存在.理由如下
设斜率为1的直线l的方程为y=x+m,代入中,
化简得:3x2+4mx+2m2﹣8=0,①
因为直线l与椭圆G相交于A,B两点,
∴△=16m2﹣12(2m2﹣8)>0,
解得﹣2,②
设A(x1,y1),B(x2,y2),则,.③
于是AB的中点M(x0,y0)满足=﹣,.
已知点P(﹣3,2),若以AB为底的等腰三角形ABP存在,
则kPM=﹣1,即=﹣1,④,将M(﹣)代入④式,
得m=3∈(﹣2,2)满足②
此时直线l的方程为y=x+3.
21.已知函数f(x)=ex﹣ax+1,其中a为实常数,e=2.71828…为自然对数的底数.
(1)当a=e时,求函数f(x)的单调区间;
(2)若函数f(x)在定义域内单调递增,求a的取值范围;
(3)已知a>0,并设函数f(x)的最小值为g(a),求证:g(a)≤2.
【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.
【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,问题转化为ex≥a恒成立,从而求出a的范围即可;
(3)求出f(x)的最小值,问题转化为只需证明gmax(a)≤2,根据函数的单调性证明即可.
【解答】解:(1)函数的定义域:R …
当a=e时,f'(x)=ex﹣e…
令f'(x)=0解得x=1,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:x<1,
所以f(x)的单调递减区间是(﹣∞,1),递增区间是(1,+∞)…
(2)因为f(x)在定义域内单调递增,
则f'(x)=ex﹣a≥0在R上恒成立…,
即ex≥a恒成立,ex>0…所以a≤0.…
(3)证明:f'(x)=ex﹣a
当a>0时令f'(x)=0,解得x=lna,
令f′(x)>0,解得:x>lna,令f′(x)<0,解得:x<lna,
∴f(x)在(﹣∞,lna)递减,在(lna,+∞)递增,
所以g(a)=fmin(x)=f(lna)=a﹣alna+1…
要证明g(a)≤2,则只需证明gmax(a)≤2…
而g'(a)=﹣lna令g'(a)=0,解得a=1,…
令g′(a)>0,解得:a<1,令g′(a)<0,解得:a>1,
所以gmax(a)=g(1)=2≤2成立.
∴g(a)≤2….
22.已知函数f(x)=lnx+ax2,其中a为实常数.
(1)讨论函数f(x)的极值点个数;
(2)若函数f(x)有两个零点,求a的取值范围.
【考点】利用导数研究函数的极值;利用导数研究函数的单调性.
【分析】(1)求导数,分类讨论,确定导数为0方程解的个数,即可讨论函数f(x)的极值点个数;
(2)由(1)可知①当a≥0时,f(x)为增函数,至多只有一个零点,不合;②当a<0时,要使得函数f(x)有两个零点,则须且只需fmax(x)>0,即可求a的取值范围.
【解答】解:(1)定义域:(0,+∞)……
①当a≥0时,因为x>0,所以f'(x)>0在定义域内恒成立,∴f(x)无极值点.…
②当a<0时,,
令f'(x)=0,则或(舍去)…
可知f(x)有一个极大值点,无极小值点.即极值点个数为1.…
综上,当a≥0时,f(x)无极值点,当a<0时,有且只有一个极值点.…
(2)由(1)可知①当a≥0时,f(x)为增函数,至多只有一个零点,不合.…
②当a<0时,,…
当x→+∞时,f(x)→﹣∞;当x→0+时,f(x)→﹣∞,…
要使得函数f(x)有两个零点,则须且只需fmax(x)>0,…
即解得,…
又a<0,所以
综上:a的取值范围是…
2017年1月24日