数学（理）卷·2017届山西省孝义市高三下学期高考考前质量检测三（5月模拟）（2017 11页

山西省孝义市2017届高三下学期高考考前质量检测三（5月模拟）‎ 理科数学 第Ⅰ卷 一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知复数，则（ ）．‎ A． 2 B． C． 4 D．‎ ‎2.已有角的顶点与坐标原点重合，始边与轴的非负半轴重合，终边经过点，则（ ）．‎ A． B． C． D．‎ ‎3.已知函数则（ ）．‎ A． B． C． D．‎ ‎4.现有4张卡片，正面分别标有1，2，3，4，背面完全相同.将卡片洗匀，背面向上放置，甲、乙二人轮流抽取卡片，每人每次抽取一张，抽取后不放回，甲先抽.若二人约定，先抽到标有偶数的卡片者获胜，则甲获胜的概率是（ ）．‎ A． B． C． D．‎ ‎5.定义：，如，则（ ）．‎ A．0 B． C．3 D．6‎ ‎6.在的展开式中，的系数是（ ）．‎ A． 55 B． 66 C．165 D．220‎ ‎7.若，且，则的最大值是（ ）．‎ A．1 B． C． D．2‎ ‎8.如果满足，则的取值范围是（ ）．‎ A． B． C． ‎ ‎ D．‎ ‎9.已知抛物线的焦点为，点，射线与交于点，与的准线交于点，且，则点到轴的距离是（ ）．‎ A． B． C． D．1‎ ‎10.已知是半径为的球面上的两点，过作互相垂直的两个平面、，若截该球所得的两个截面的面积之和为，则线段的长度是（ ）．‎ A． B．2 C． D．4‎ ‎11.水车在古代是进行灌溉引水的工具，是人类的一项古老的发明，也是人类利用自然和改造自然的象征.如图是一个半径为的水车，一个水斗从点出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时60秒.经过秒后，水斗旋转到点，设的坐标为，其纵坐标满足.则下列叙述错误的是（ ）．‎ A． B．当时，点到轴的距离的最大值为6‎ C．当时，函数单调递减 D．当时，‎ ‎12.若关于的不等式的解集为，且，则整数的最大值是（ ）．‎ A．3 B．4 C．5 D．6‎ 第Ⅱ卷 二、填空题：本大题共4小题 ，每小题5分，满分20分，将答案填在答题纸上 ‎13.已知集合，则____________．‎ ‎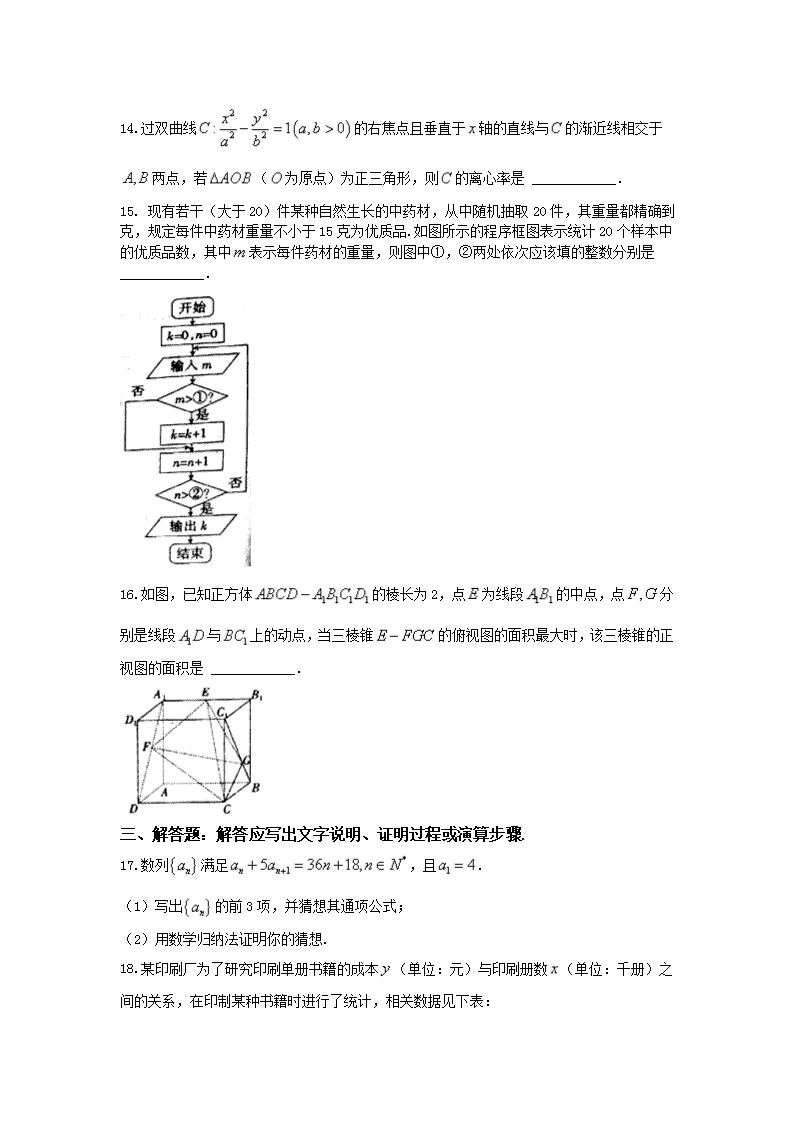14.过双曲线的右焦点且垂直于轴的直线与的渐近线相交于两点，若（为原点）为正三角形，则的离心率是 ____________．‎ ‎15. 现有若干（大于20）件某种自然生长的中药材，从中随机抽取20件，其重量都精确到克，规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数，其中表示每件药材的重量，则图中①，②两处依次应该填的整数分别是____________．‎ ‎16.如图，已知正方体的棱长为2，点为线段的中点，点分别是线段与上的动点，当三棱锥的俯视图的面积最大时，该三棱锥的正视图的面积是 ____________．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤. ‎ ‎17.数列满足，且.‎ ‎（1）写出的前3项，并猜想其通项公式；‎ ‎（2）用数学归纳法证明你的猜想.‎ ‎18.某印刷厂为了研究印刷单册书籍的成本（单位：元）与印刷册数（单位：千册）之间的关系，在印制某种书籍时进行了统计，相关数据见下表：‎ 印刷册数（千册）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 单册成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.7‎ 根据以上数据，技术人员分别借助甲、乙两种不同的回归模型，得到两个回归方程，方程甲：，方程乙：.‎ ‎（1）为了评价两种模型的拟合效果，完成以下任务.‎ ‎①完成下表（计算结果精确到0.1）；‎ 印刷册数（千册）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 单册成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.7‎ 模型甲 估计值 ‎2.4‎ ‎2.1‎ ‎1.6‎ 残差 ‎0‎ ‎-0.1‎ ‎0.1‎ 模型乙 估计值 ‎2.3‎ ‎2‎ ‎1.9‎ 残差 ‎0.1‎ ‎0‎ ‎0‎ ‎②分别计算模型甲与模型乙的残差平方和及，并通过比较，的大小，判断哪个模型拟合效果更好.‎ ‎（2）该书上市之后，受到广大读者热烈欢迎，不久便全部售罄，于是印刷厂决定进行二次印刷.根据市场调查，新需求量为8千册（概率0.8）或10千册（概率0.2），若印刷厂以每册5元的价格将书籍出售给订货商，问印刷厂二次印刷8千册还是10千册能获得更多利润？（按（1）中拟合效果较好的模型计算印刷单册书的成本）‎ ‎19.如图（1），五边形中，.如图（2），将沿折到的位置，得到四棱锥.点为线段的中点，且平面．‎ ‎（1）求证：平面平面；‎ ‎（2）若直线与所成角的正切值为，求直线与平面所成角的正弦值．‎ ‎20. 已知椭圆的离心率为，且过点．‎ ‎（1）求的方程；‎ ‎（2）若直线与相交于两点，且与（为坐标原点）的斜率之和为2，求到直线距离的取值范围．‎ ‎21. 已知函数.‎ ‎（1）讨论函数的单调性；‎ ‎（2）证明：‎ 请考生在22、23三题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 已知直线（其中为参数，为倾斜角）.以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求的直角坐标方程，并求的焦点的直角坐标；‎ ‎（2）已知点，若直线与相交于两点，且，求的面积.‎ ‎23.选修4-5：不等式选讲 已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若，试证：.‎ 参考答案 一、 A卷选择题 ‎ ‎1－5 AAADA 6－10 DCDBD 11－12 CB 二、 填空题 ‎13. 14. 15. 14，19 16. 2‎ 三、解答题 ‎17.解：（1），猜想；‎ ‎（2）①当时，成立；‎ ‎②假设时，猜想成立，即有，‎ 由，，及，‎ 得，即当时猜想成立，‎ 由①②可知，对一切正整数均成立.‎ ‎18.解：（1）①经计算，可得下表：‎ 印刷册数（千册）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 单册成本（元）‎ ‎3.2‎ ‎2.4‎ ‎2‎ ‎1.9‎ ‎1.7‎ 模型甲 估计值 ‎3.1‎ ‎2.4‎ ‎2.1‎ ‎1.9‎ ‎1.6‎ 残差 ‎0.1‎ ‎0‎ ‎-0.1‎ ‎0‎ ‎0.1‎ 模型乙 估计值 ‎3.2‎ ‎2.3‎ ‎2‎ ‎1.9‎ ‎1.7‎ 残差 ‎0‎ ‎0.1‎ ‎0‎ ‎0‎ ‎0‎ ‎②，故模型乙的拟合效果更好；‎ ‎（2）若二次印刷8千册，则印刷厂获利为（元），‎ 若二次印刷10千册，由（1）可知，单册书印刷成本为（元）‎ 故印刷总成本为16640（元），‎ 设新需求量为（千册），印刷厂利润为（元），则 ‎8‎ ‎10‎ ‎0.8‎ ‎0.2‎ ‎,‎ 故，‎ 故印刷8千册对印刷厂更有利.‎ ‎19.（1）证明：取的中点，连接，则，‎ 又，所以，则四边形为平行四边形，所以，‎ 又平面，‎ ‎∴平面，‎ ‎∴.‎ 由即及为的中点，可得为等边三角形，‎ ‎∴，‎ 又，∴，∴，‎ ‎∴平面平面，‎ ‎∴平面平面.‎ ‎（2）解：‎ ‎，∴为直线与所成的角，‎ 由（1）可得，∴，∴，‎ 设，则，‎ 取的中点，连接，过作的平行线，‎ 可建立如图所示的空间直角坐标系，‎ 则，‎ ‎∴，‎ 所以，‎ 设为平面的法向量，则，即，‎ 取，则为平面的一个法向量，‎ ‎∵，‎ 则直线与平面所成角的正弦值为.‎ ‎20.解：（1）由已知得，‎ 解得，∴椭圆的方程为；‎ ‎（2）把代入的方程得：‎ ‎，‎ 其判别式，①‎ 设，则，②‎ 由已知得，‎ ‎∴，③‎ 把②代入③得，‎ 即，④‎ 把④代入①及知，‎ 又，∴，‎ 点到直线的距离为，‎ 当时，；‎ 当时，，‎ 令，则，‎ 设，则，∴在单调递减，‎ ‎∴当时，，‎ 综上，点到直线的距离的取值范围为.‎ ‎21.（1）解：，‎ ‎①若时，在上单调递减；‎ ‎②若时，当时，单调递减；‎ 当时，单调递增；‎ 综上，若时，在上单调递减；‎ 若时，在上单调递减；‎ 在上单调递增；‎ ‎（2）证明：要证，只需证，‎ 由（1）可知当时，，即，‎ 当时，上式两边取以为底的对数，可得，‎ 用代替可得，又可得，‎ 所以，‎ ‎，‎ 即原不等式成立.‎ ‎22.解：（1）原方程变形为，‎ ‎∵，‎ ‎∴的直角坐标方程为，其焦点为.‎ ‎（2）把的方程代入得，‎ 则，①‎ ‎，‎ 即，‎ 平方得，②‎ 把①代入②得，∴，‎ ‎∵是直线的倾斜角，∴，‎ ‎∴的普通方程为，且，‎ ‎∴的面积为.‎ ‎23.（1）解：不等式可以转化为 或或，‎ 解得，‎ 即不等式的解集.‎ ‎（2）证明：因为，‎ 又因为，所以，‎ 所以，当且仅当时，等号成立，‎ 即，得证.‎