2017-2018学年河南省郑州市第一中学高二下学期期中考试数学（理）试题（解析版） 15页

‎2017-2018学年河南省郑州市第一中学高二下学期期中考试数学（理）试题 一、单选题 ‎1．设，若复数（是虚数单位）的实部为，则的值为（ ）‎ A. B. C. 1 D. -1‎ ‎【答案】C ‎【解析】分析：‎ 将复数分母实数化得到实部，令其等于，即可得解.‎ 详解：‎ 复数.‎ 实部为，所以.解得.‎ 故选C.‎ 点睛：本题考查了复数的除法运算和实部的概念，属于基础题.‎ ‎2．函数的图象在点处的切线方程为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】f′(x)＝，则f′(1)＝1，‎ 故函数f(x)在点(1，－2)处的切线方程为y－(－2)＝x－1，即x－y－3＝0.‎ 故选：C ‎3．用反证法证明命题：“三角形的内角中至少有一个不大于”时，假设正确的是（ ）‎ A. 假设三内角都不大于 B. 假设三内角都大于 C. 假设三内角至多有一个大于 D. 假设三内角至多有两个大于 ‎【答案】B ‎【解析】分析：‎ 根据“至少有一个”的否定：“一个也没有”可得解.‎ 详解：‎ 根据反证法的步骤，假设是对原命题结论的否定，“至少有一个”的否定：“一个也没有”；即“三内角都大于60度”.‎ 故选B.‎ 点睛：一些正面词语的否定：“是”的否定：“不是”；“能”的否定：“不能”；“都是”的否定：“不都是”； “至多有一个”的否定：“至少有两个”；“至少有一个”的否定：“一个也没有”；“是至多有n个”的否定：“至少有n+1个”；“任意的”的否定：“某个”；“任意两个”的否定：“某两个”；“所有的”的否定：“某些”．‎ ‎4．已知为虚数单位，若复数（）的模为该复数的实部的倍，则（ ）‎ A. 0 B. -4 C. 1或-1 D. 1‎ ‎【答案】A ‎【解析】分析：‎ 将复数分母实数化得到模和实部，建立方程可得解.‎ 详解：‎ 复数.模为：.‎ 根据题意得：.解得.‎ 故选A.‎ 点睛：本题考查了复数的除法运算和模的计算，实部的概念，属于基础题.‎ ‎5．由抛物线和直线所围成的封闭图形的面积等于（ ）‎ A. 1 B. C. D. 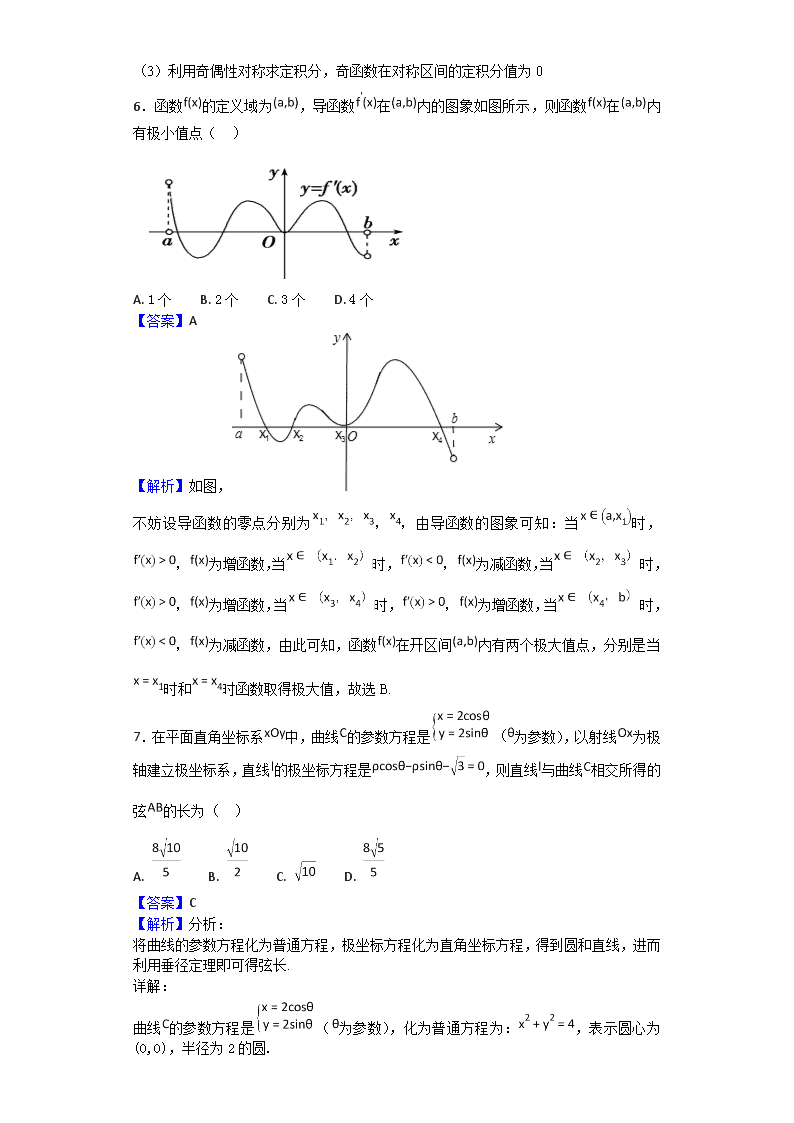‎ ‎【答案】B ‎【解析】分析：‎ 由定积分的几何意义可求封闭图形的面积.‎ 详解：‎ 联立，解得和.‎ 所以抛物线和直线所围成的封闭图形的面积等于 ‎.‎ 故选B.‎ 点睛：‎ 定积分的计算一般有三个方法：‎ ‎（1）利用微积分基本定理求原函数；‎ ‎（2）利用定积分的几何意义，利用面积求定积分；‎ ‎（3）利用奇偶性对称求定积分，奇函数在对称区间的定积分值为0‎ ‎6．函数的定义域为，导函数在内的图象如图所示，则函数在内有极小值点（ ）‎ A. 1个 B. 2个 C. 3个 D. 4个 ‎【答案】A ‎【解析】如图，‎ 不妨设导函数的零点分别为，，由导函数的图象可知：当时，，为增函数，当时，，为减函数，当时，，为增函数，当时，，为增函数，当时，，为减函数，由此可知，函数在开区间内有两个极大值点，分别是当时和时函数取得极大值，故选B.‎ ‎7．在平面直角坐标系中，曲线的参数方程是（为参数），以射线为极轴建立极坐标系，直线的极坐标方程是，则直线与曲线相交所得的弦的长为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：‎ 将曲线的参数方程化为普通方程，极坐标方程化为直角坐标方程，得到圆和直线，进而利用垂径定理即可得弦长.‎ 详解：‎ 曲线的参数方程是（为参数），化为普通方程为：，表示圆心为(0,0)，半径为2的圆.‎ 直线的极坐标方程是，化为直角坐标方程即为：.‎ 圆心到直线的距离为：.‎ 直线与曲线相交所得的弦的长为:.‎ 故选：D.‎ 点睛：‎ 直线与圆的位置关系常用处理方法：‎ ‎（１）直线与圆相切处理时要利用圆心与切点连线垂直，构建直角三角形，进而利用勾股定理可以建立等量关系；‎ ‎（２）直线与圆相交，利用垂径定理也可以构建直角三角形；‎ ‎（３）直线与圆相离时，当过圆心作直线垂线时长度最小．‎ ‎8．郑州市了为缓解交通压力，实行机动车辆限行政策，每辆机动车每周一到周五都要限行一天，周末（周六和周日）不限行，某公司有五辆车，保证每天至少有四辆车可以上路行驶，已知车周四限行，车昨天限行，从今天算起，两车连续四天都能上路行驶，车明天可以上路，由此可知下列推测一定正确的是（ ）‎ A. 今天是周六 B. 今天是周四 C. 车周三限行 D. 车周五限行 ‎【答案】B ‎【解析】分析：‎ 根据已知中E车限行情况可得今天不是周三，根据B车限行情况可得今天不是周一，不是周日，根据AC车的限行情况可知今天不是周五，周二和周六．‎ 详解：‎ ‎∵保证每天至少有四辆车可以上路行驶，‎ E车明天可以上路且E车周四限行，可知：今天不是周三，‎ B车昨天限行，今天不是周一，不是周日，‎ A.C两车连续四天都能上路行驶，今天不是周五，周二和周六，‎ 由此推出今天是周四，‎ 故选：B 点睛：本题主要考查了学生的逻辑推理能力，做此类题型时，通常是选取价值较高的信息开始假设或推理.‎ ‎9．若函数在单调递增，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：‎ 由函数单增等价转换为导函数大于等于0恒成立，通过二倍角化简，进而换元为二次不等式恒成立即可.‎ 详解：‎ 若函数在单调递增，则在上恒成立.‎ 即在上恒成立，即恒成立.‎ 令，原命题等价于在恒成立.‎ 只需，解得：.‎ 故选C.‎ 点睛：利用导数解决不等式恒成立问题的“两种”常用方法 ‎（1）分离参数法：将原不等式分离参数，转化为不含参数的函数的最值问题，利用导数求该函数的最值，根据要求得所求范围.一般地，f(x)≥a恒成立，只需f(x)min≥a即可；f(x)≤a恒成立，只需f(x)max≤a即可.‎ ‎(2)函数思想法：将不等式转化为某含待求参数的函数的最值问题，利用导数求该函数的极值(最值)，然后构建不等式求解.‎ ‎10．若函数在内有极小值，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】分析：‎ 求得函数导数，令导数为0，得极小值点，使其属于，即可得解．‎ 详解：‎ 由题意得,函数的导数.‎ 当时，令，解得 分析单调性可知，为函数的极小值点.‎ 根据题意知：，解得：.‎ 故选：D.‎ 点睛：‎ 求函数极值的步骤：(1) 确定函数的定义域；(2) 求导数；(3) 解方程求出函数定义域内的所有根；(4) 列表检查在的根左右两侧值的符号，如果左正右负（左增右减），那么在处取极大值，如果左负右正（左减右增），那么在处取极小值.‎ ‎11．给出下面类比推理命题（其中为有理数，为实数集，为复数集）：‎ ‎①“若，则”类比推出“，则”；‎ ‎②“若，则复数”类比推出“，则”；‎ ‎③“若，则”类比推出“若，则”；‎ ‎④“若，则”类比推出“若，则”；‎ 其中类比结论正确的个数有（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】B ‎【解析】很明显命题①②正确，‎ 对于命题③，当时，，但是无法比较的大小，原命题错误；‎ 对于命题④，若，则，但是无法比较z与1,-1的大小，原命题错误；‎ 综上可得，类比结论正确个数为2.‎ 本题选择B选项.‎ 点睛：在进行类比推理时，要尽量从本质上去类比，不要被表面现象所迷惑；否则只抓住一点表面现象甚至假象就去类比，就会犯机械类比的错误．‎ ‎12．对于函数和，设，，若存在使得，则称和互为“友邻函数”，若函数与互为“友邻函数”，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】分析：‎ 易得的零点为，由函数零点的关系知在区间上有零点，结合函数过点(-2,9)，可利用二次函数根的分布得解.‎ 详解：‎ 令，解得，‎ 由题意知，在区间上有零点.‎ 因为恒过点(-2,9).‎ ‎，得.‎ ‎，解得.‎ 综上可得：.‎ 故选D.‎ 点睛：解本题的关键是处理二次函数在区间上大于0的有解问题，对于二次函数的研究一般从以几个方面研究：‎ 一是，开口；‎ 二是，对称轴，主要讨论对称轴与区间的位置关系；‎ 三是，判别式，决定于x轴的交点个数；‎ 四是，区间端点值.‎ 二、填空题 ‎13．一质点沿直线运动，如果由始点起经过秒后的位移为，那么这个质点在2秒末的瞬时速度是__________．‎ ‎【答案】0‎ ‎【解析】分析：位移对时间求导数即是速度，求出位移的导数，令代入求解即可．‎ 详解：‎ ‎∵，‎ ‎∴，‎ 这个质点在2秒末的瞬时速度是 故答案为：0.‎ 点睛：本题主要考查导数的物理意义，位移对时间求导可得瞬时速度.‎ ‎14．有一个奇数列……，现在进行如下分组：第一组含一个数，第二组合含两个数；第三组含三个数；第四组含四个数……；则观察每组内各数之和与组的编号数的关系式为__________．‎ ‎【答案】‎ ‎【解析】分析：由题意先计算第一、二、三组内各数之和与其组的编号数的关系，再猜想．‎ 详解：‎ 由题意，1=13，‎ ‎3+5=23，‎ ‎7+9+11=33，‎ ‎…‎ 故可得每组内各数之和与其组的编号数n的关系为，‎ 故答案为：.‎ 点睛：本题主要考查了学生的归纳的能力，属于简单题.‎ ‎15．以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，则在直角坐标系下曲线的方程为__________．‎ ‎【答案】‎ ‎【解析】分析：利用代入方程化简可得解.‎ 详解：‎ 利用代入可得：.‎ 化简得：.‎ 故答案为：.‎ 点睛：极坐标方程化为直角坐标方程时常通过变形，构造形如的形式，进行整体代换.其中方程的两边同乘以(或同除以) 及方程两边平方是常用的变形方法.‎ ‎16．定义在上的函数满足：，，是的导函数，则不等式（其中为自然对数的底数）的解集为_______.‎ ‎【答案】‎ ‎【解析】试题分析：设 所以为增函数时，即，所以不等式的解集为 ‎（0，+∞）‎ ‎【考点】1．函数导数与单调性；2．不等式与函数的转化 三、解答题 ‎17．（1）设（是虚数单位），求的值.‎ ‎（2）设，复数，且满足，试求的值.‎ ‎【答案】(1) (2) ‎ ‎【解析】分析：（1）利用复数的除法和乘方运算法则求解即可；‎ ‎（2）化简方程得，从而得，解方程组即可.‎ 详解：‎ ‎（1）‎ ‎（2）将代入，得 ‎∴，∴‎ 点睛：对于复数的运算一是要注意运算的顺序，另外要注意在运算中的应用，即遇到时要写成．求复数的模时，首项将复数化为代数形式后再根据公式求解．‎ ‎18．求由曲线，，所围成的封闭图形的面积.‎ ‎【答案】‎ ‎【解析】试题分析：求出曲线的交点横坐标,求出的交点的横坐标,再分成两部分算出阴影部分的面积.‎ 试题解析:联立求出,联立求出,所以阴影部分面积.‎ ‎【考点】1.用定积分算阴影部分面积的步骤；2.微积分基本定理.‎ ‎19．已知， ， ．‎ ‎（1）当时，试比较与的大小关系；‎ ‎（2）猜想与的大小关系，并给出证明．‎ ‎【答案】21.解：（1） 当时， ， ，所以；‎ 当时， ， ，所以；‎ 当时， ， ，所以．………3分 ‎（2）由（１），猜想，下面用数学归纳法给出证明：‎ ‎①当时，不等式显然成立．‎ ‎②假设当时不等式成立，即，....6分 那么，当时，，‎ 因为，‎ 所以．‎ 由①、②可知，对一切，都有成立．………………12分 ‎【解析】试题分析：（1）分别计算,在比较大小．（2）由（1）猜想．用数学归纳法证明．‎ 试题解析：（1）当时， ，所以；‎ 当时， ，所以；‎ 当时， ，所以．‎ ‎（2）由（1）猜想,下面用数学归纳法给出证明:‎ 当时,不等式显然成立．‎ 假设当时不等式成立,即,‎ 那么当时, ,‎ 因为,‎ 所以,‎ 综上可得,对一切,都有成立．‎ ‎【考点】数学归纳法．‎ ‎20．设函数，.‎ ‎（1）若关于的方程有3个不同实根，求实数的取值范围；‎ ‎（2）已知当时，恒成立，求实数的取值范围.‎ ‎【答案】(1) (2) ‎ ‎【解析】分析：‎ ‎（1）求函数导数，进而得函数单调性，从而结合图像即可得解；‎ ‎（2）当时，恒成立，可化简为在上恒成立，令，求函数最小值即可.‎ 详解：‎ ‎（1），令，得，‎ ‎∴当或时，；当时，，‎ ‎∴的单调递增区间是和，单调递减区间是 当，有极大值；‎ 当，有极小值.‎ 可知图象的大致形状及走向 ‎∴当时，直线与的图象有3个不同交点，‎ 即当时方程有三解.‎ ‎（2）即 ‎∵，∴在上恒成立.‎ 令，由二次函数的性质，在上是增函数，‎ ‎ ∴，∴所求的取值范围是 点睛：利用导数解决不等式恒成立问题的“两种”常用方法 ‎（1）分离参数法：将原不等式分离参数，转化为不含参数的函数的最值问题，利用导数求该函数的最值，根据要求得所求范围.一般地，f(x)≥a恒成立，只需f(x)min≥a即可；f(x)≤a恒成立，只需f(x)max≤a即可.‎ ‎(2)函数思想法：将不等式转化为某含待求参数的函数的最值问题，利用导数求该函数的极值(最值)，然后构建不等式求解.‎ ‎21．已知函数（）.‎ ‎（1）当时，求的单调区间和极值；‎ ‎（2）若，且，证明：‎ ‎【答案】(1) 函数的单调递减区间是，单调递增区间是，在区间上的极小值为，无极大值；(2)见解析 ‎【解析】分析：‎ ‎（1）求函数导数，讨论时，时，结合导函数的零点及正负可得极值和单调区间；‎ ‎（2）由（1）知，，要证，只要证，即证，在区间上单调递增，所以，又，即证，构造函数，结合函数单调性可得证.‎ 详解：‎ ‎（1），‎ ‎①时，因为，所以 函数的单调递增区间是，无单调递减区间，无极值；‎ ‎②当时，令，解得，‎ 当时，；当，.‎ 所以函数的单调递减区间是，单调递增区间是，‎ 在区间上的极小值为，无极大值.‎ ‎（2）因为，由（1）知，函数在区间上单调递减，‎ 在区间上单调递增，‎ 不妨设，则，‎ 要证，只要证，即证 因为在区间上单调递增，所以，‎ 又，即证，‎ 构造函数，‎ 即，.‎ ‎，‎ 因为，所以，，即，‎ 所以函数在区间上单调递增，故，‎ 而，故，‎ 所以，即，所以成立.‎ 点睛：利用函数导数证明不等式的关键是构造函数，主要有两类：一元不等式证明和多元不等式证明.‎ 一元不等式证明的主要方法有：（1）构造差函数；（2）构建了两个函数比较大小；‎ 多元不等式证明，首先要多元换一元，再继续证明.‎ ‎22．选修4-4：坐标系与参数方程 在直角坐标系中，直线的参数方程为（为参数），在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，圆的方程为.‎ ‎（1）求圆的直角坐标方程；‎ ‎（2）设圆与直线交于点，求的最小值.‎ ‎【答案】(1) (2) ‎ ‎【解析】分析：‎ ‎（1）由得，利用，即可得解；‎ ‎（2）将的参数方程代入圆的直角坐标方程，得，由，结合韦达定理即可得解.‎ 详解：‎ ‎（1）由得，‎ 化为直角坐标方程为，即 所以圆的直角坐标方程为.‎ ‎（2）将的参数方程代入圆的直角坐标方程，得，‎ 由已知得，所以可设是上述方程的两根，‎ 则，‎ ‎ .‎ 所以的最小值为.‎ 点睛：本题主要考查了直角坐标与极坐标的互化，直线的参数方程的应用，属于基础题.‎ ‎23．选修4-5：不等式选讲 已知不等式.‎ ‎（1）若，求不等式的解集；‎ ‎（2）若已知不等式的解集不是空集，求的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】试题分析：（1）结合函数的解析式，由零点分段法进行分类讨论，即可得到不等式的解集；（2）化简函数的解析式，作出函数的图象，通过图象即可求出的取值范围.‎ 试题解析：（1）当时，不等式即为，‎ 若，则， ，∴舍去；‎ 若，则，∴；‎ 若，则，∴.‎ 综上，不等式的解集为 ‎（2）设，则作出函数的图象，如图所示.‎ 由图象可知， ，∴， ，即的取值范围为.‎