- 95.93 KB
- 2021-06-24 发布
2016-2017学年江西省赣州市寻乌中学高二上学期第三次月考理科数学
一、选择题:共12题
1.下列命题错误的是
A.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
B.若命题p:∃x0∈R,x02-x0+1≤0,则¬p:∀x∈R,x2-x+1>0
C.ΔABC中,sinA>sinB是A>B的充要条件
D.若p∧q为假命题,则p,q均为假命题
【答案】D
【解析】本题考查命题及其关系,全称命题与特称命题,逻辑连接词。A正确;特称命题的否定是全称命题,B正确;ΔABC中,由正弦定理得sinA>sinBa>bA>B,所以C正确;若p∧q为假命题,则p,q至少有一个为假命题,D错误。选D。
2.命题“∃x0∈R,使得x02+2x0+5=0”的否定是
A.∀x∈R,x2+2x+5=0 B.∀x∈R,x2+2x+5≠0
C.∀x∉R,x2+2x+5=0 D.∀x∉R,x2+2x+5≠0
【答案】B
【解析】本题主要考查特称命题的否定.
特称命题的否定是全称命题. 则命题“∃x0∈R,使得x02+2x0+5=0”的否定是:∀x∈R,x2+2x+5≠0.
故选B.
3.设l是空间一条直线,α和β是两个不同的平面,则下列结论正确的是
A.若l//α,l//β,则α//β B.若α⊥β,l//α,则l⊥β
C.若α⊥β,l⊥α,则l//β D.若l//α,l⊥β,则α⊥β
【答案】D
【解析】本题主要考查空间中线面、面面之间的位置关系.
对于A,若l//α,l//β,则α与β相交或平行,故A错误;
对于B,若α⊥β,l//α,则l与β相交、平行或l⊂β,故B错误;
对于C,若α⊥β,l⊥α,则l与β相交、平行或l⊂β,故C错误;
对于D,若l//α,l⊥β,则由面面垂直的判定可得α⊥β,故D正确.
故选D.
4.“直线ax+3y+1=0与直线2x+(a+1)y+1=0平行”是“a=-3”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【解析】本题主要考查充分必要条件和两直线的关系.
若直线ax+3y+1=0与直线2x+(a+1)y+1=0平行,
则由aa+1-2×3=03×1-a+1×1≠0,得a=-3.
若a=-3,则两直线为:-3x+3y+1=0与2x-2y+1=0,平行.
故“直线ax+3y+1=0与直线2x+(a+1)y+1=0平行”是“a=-3”的充要条件.
故选C.
5.若椭圆的焦距与短轴长相等,则此椭圆的离心率为
A.15 B.55 C.12 D.22
【答案】B
【解析】本题主要考查椭圆的性质.
若椭圆的焦距与短轴长相等,则2c=2b,又a2=b2+c2,
则c2a2=c22a2=12,
则此椭圆的离心率为e=ca=22.
故选B.
6.与曲线x224+y249=1有相同的焦点,且与曲线x236-y264=1共渐近线的双曲线方程是
A.x216-y29=1 B.y216-x29=1 C.x29-y216=1 D.y29-x16=1
【答案】B
【解析】本题主要考查椭圆、双曲线的标准方程和性质.
由题知,双曲线的焦点坐标为0,±5,渐近线方程是y=±43x,
∴a=4,b=3,c=5,∴所求双曲线方程是y216-x29=1.
故选B.
7.抛物线y=x2上到直线2x-y-4=0距离最近的点的坐标是
A.(1,1) B.(12,14) C.(13,19) D.(2,4)
【答案】C
【解析】本题主要考查点到直线的距离公式及二次函数的最值.
设P(x,y)为抛物线上任意一点,
则P到直线的距离为d=2x-y-44+1=2x-x2-45=(x-1)2+35,
当x=1时,d取得最小值.此时,P(1,1).
故选C.
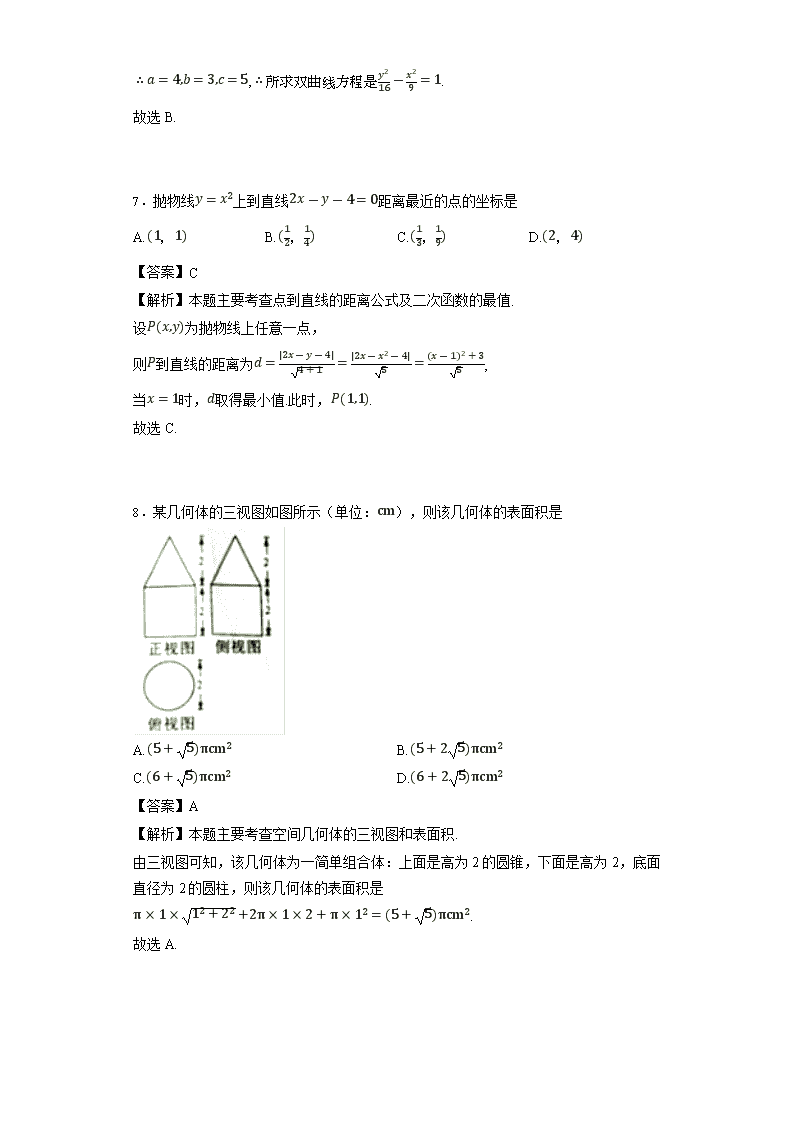
8.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是
A.(5+5)πcm2 B.(5+25)πcm2
C.(6+5)πcm2 D.(6+25)πcm2
【答案】A
【解析】本题主要考查空间几何体的三视图和表面积.
由三视图可知,该几何体为一简单组合体:上面是高为2的圆锥,下面是高为2,底面直径为2的圆柱,则该几何体的表面积是
π×1×12+22+2π×1×2+π×12=(5+5)πcm2.
故选A.
9.已知△ABC在平面α内,直线CD⊥平面α,P是平面α内的一个动点,设P到直线AB的距离为d1,P到直线CD的距离为d2,若d1=d2,则动点P的轨迹是
A.圆 B.椭圆 C.双曲线 D.抛物线
【答案】D
【解析】本题主要考查抛物线的定义.
由题知,P到直线CD的距离就是P到点C的距离,由抛物线的定义可得结论.
故选D.
10.过点(2,3)作圆(x+4)2+(y+1)2=9的切线PA,PB,切点分别是A,B,则直线AB的方程为
A.6x+4y+19=0 B.4x-6y+19=0
C.6x-4y+19=0 D.4x+6y-19=0
【答案】A
【解析】本题主要考查求过圆的两切点的直线方程.
圆心为P(-4,-1),M(2,3),以PM为直径的圆的方程为(x+1)2+(y-1)2=13,即x2+y2+2x-2y-11=0,
将两圆方程相减得6x+4y+19=0.则这条直线过两圆的交点即切点A,B,则6x+4y+19=0就是直线AB的方程.
故选A.
11.已知A(-2,0),B(2,0),P(x,y),下列命题正确的是
A.若P到A,B的距离之和为4,则点P的轨迹为椭圆
B.若P到A,B的距离之差为3,则点P的轨迹为双曲线
C.椭圆x24+y23=1上任意一点M(长轴端点除外)与A,B连线斜率之积为-34
D.双曲线x24-y23=1上任意一点M(实轴端点除外)与A,B连线斜率之积为-34
【答案】C
【解析】本题主要考查椭圆、双曲线的定义,直线的斜率及同角三角函数的基本关系.
AB=4,
对于A,点P的轨迹为线段AB,故A错误;
对于B,点P的轨迹为双曲线的左支,故B错误;
对于C,A(2,0),B2,0为椭圆长轴端点,设M2cosθ,3sinθ,则
kMA∙kMB=3sinθ2cosθ+2∙3sinθ2cosθ-2=3sin2θ4(cos2θ-1)=-34,故C正确;
对于D,A(2,0),B2,0为双曲线实轴端点,设M2cosα,3tanα,则
kMA∙kMB=3tanα2cosα+2∙3tanα2cosα-2=3tan2α4(1cos2α-1)=34,,故D错误.
故选C.
12.过正方体ABCD-A1B1C1D1的顶点A作直线,使与直线AD1所成的角为30°,且与平面C1D1C所成的角为60°,则这样的直线的条数是
A.1 B.2 C.3 D.4
【答案】B
【解析】本题主要考查空间中线线、线面所成的角.
在平面C1D1C内,以D为圆心,以33AB为半径画圆,则点A与此圆上的点的连线满足与平面C1D1C所成的角为60°,其中,满足与直线AD1所成的角为30°的直线有且只有两条.
故选B.
二、填空题:共4题
13.抛物线y=2x2的焦点坐标为 .
【答案】(0,18)
【解析】本题主要考查抛物线的标准方程和性质.
由y=2x2得x2=12y,则抛物线y=2x2的焦点坐标为(0,18).
故答案为(0,18)
14.若直线2x+ay-7=0与直线(a-3)x+y+4=0互相垂直,则实数a= .
【答案】2
【解析】本题主要考查两直线垂直的表示.
由题得,2(a-3)+a×1=0,解得a=2.
故答案为2.
15.三棱锥D-ABC的四个顶点在同一球面上,AC⊥AB,△DBC是边长为4的正三角形,若平面ABC⊥平面DBC,则该球的表面积为 .
【答案】64π3
【解析】本题主要考查球的表面积.
∵AC⊥AB,BC=4,∴△ABC外接圆的半径为2,
∵平面ABC⊥平面DBC,∴球心在BC边的高上,
设球心到平面ABC的距离为h,则h2+3=R2=23-h2,∴R=433,
则该球的表面积S=4πR2=64π3.
故答案为64π3.
16.已知F1,F2分别为双曲线x2a2-y2b2=1(a>0,b>0)的左右焦点,过F2作双曲线一条渐近线的垂线,垂足为M,且|MF1|=3|MF2|,则此双曲线的离心率是 .
【答案】62
【解析】本题主要考查双曲线的性质和余弦定理.
设双曲线的一条渐近线为y=bax,
F2c,0到渐近线的距离d=|MF2|=bca2+b2=b,
cos∠MOF2=MOOF2=c2-b2c=ac,
在∆MOF1中,MF12=MO2+OF12-2MO∙OF1∙cos∠MOF1
=a2+c2-2ac∙-ac=3a2+c2,
由|MF1|=3|MF2|得3a2+c2=9b2=9c2-a2,即c2=32a2,
∴e=ca=62.
故答案为62.
三、解答题:共6题
17.已知命题p:关于x的方程x2-2mx+1=0有实数根;命题q:双曲线y25-x2m=1的离心率e∈(1,2),若¬q与p∧q均为假命题,求实数m的取值范围.
【答案】若命题p为真,则有Δ=4m2-4≥0,解得m≤-1或m≥1,
当p为假时有-15 5+m<20,解得00,
y1+y2=4m,y1y2=-24,x1x2=y124⋅y224=36.
于是OA⋅OB=x1x2+y1y2=12.
(2)S△OAB=12|OM|⋅|y1-y2|=3(y1+y2)2-4y1y2=316m2+96=12m2+6=1210.
m2=4,m=±2.
那么直线l的方程为x+2y-6=0和x-2y-6=0.
【解析】本题主要考查直线与抛物线的位置关系、平面向量的数量积及三角形面积.
(1)设出直线l的方程及A、B的坐标,直线与抛物线方程联立,利用韦达定理及向量数量积的坐标表示可得结论;
(2)利用三角形面积公式及(1)的结论求出直线的方程中的参数,即得直线的方程.
21.如图,在棱长为a的正方体OABC-O1A1B1C1中,点E,F分别是棱AB,BC上的动点,且AE=BF.
(1)求证:A1F⊥C1E;
(2)当三棱锥B1-EFB的体积取得最大值时,求二面角B-B1E-F的正切值.
【答案】(1)如图,建立空间直角坐标系B-xyz,
设AE=BF=m(0≤m≤a),则E(0,a-m,0),C1(a,0,a),C1(a,0,a),F(m,0,0).
∴A1F=(m,-a,-a),C1E=(-a,a-m,-a).
∴A1F⋅C1E=-am-a2+am+a2=0,
∴A1F⊥C1E.
(2)∵BB1⊥平面EFB,∴VB1-EFB=13S△BEF⋅BB1=a6m(a-m)≤a324,
当且仅当m=a2时,VB1-EFB取最大值.
此时,E(0,a2,0),F(a2,0,0),B1(0,0,a),B1E=(0,a2,-a),B1F=(a2,0,-a),
设平面B1EF的一个法向量为m=(x,y,z),
则有m⋅B1E=0m⋅B1F=0,即a2y-az=0a2x-az=0,
令x=2,则y=2,z=1,得m=(2,2,1),
取平面BB1E的一个法向量n=(1,0,0),
则cos=m⋅n|m||n|=23.二面角B-B1E-F的正切值为52.
【解析】本题主要考查利用空间向量证明线线垂直、求面面角,考查三棱锥的体积和基本不等式的应用.
(1)建立空间直角坐标系B-xyz,设AE=BF=m(0≤m≤a),验证A1F⋅C1E=0,即可得到结论;
(2)由棱锥体积公式及基本不等式得到三棱锥体积取得最大值时的条件,分别求出平面B1EF和平面BB1E的一个法向量,利用向量的夹角公式及同角三角函数的基本关系可得二面角的正切值.
22.已知A(2,0),O为坐标原点,动点P满足|OP+OA|+|OP-OA|=42.
(1)求动点P的轨迹C的方程;
(2)过点A且不垂直于坐标轴的直线交轨迹C于不同的两点M,N,线段MN的垂直平分线与x轴交于点D,线段MN的中点为H,求|DHMN|的取值范围.
【答案】(1)设P(x,y),由已知得(x+2)2+y2+(x-2)2+y2=42,
根据椭圆定义知P点轨迹为以(2,0)和(-2,0)为焦点,长轴长为42的椭圆,其方程为x28+y24=1.
(2)设直线l的斜率为k(k≠0),M(x1,y1),N(x2,y2),
则l的方程为y=k(x-2),将其代入x28+y24=1,整理得(1+2k2)x2-8k2x+8k2-8=0,
由于A在椭圆内,当然对任意实数k都有Δ>0,
根据韦达定理得x1+x2=8k21+2k2,x1x2=8k2-81+2k2,
那么|MN|=(1+k2)(x2-x1)2=(1+k2)[(x2+x1)2-4x1x2]=(1+k2)[(8k21+2k2)2-4⋅8k2-81+2k2]=42(k2+1)1+2k2.
y1+y2=k(x1-2)+k(x2-2)=k(x1+x2)-4k=-4k1+2k2,
线段MN中点H的坐标为(4k21+2k2,-2k1+2k2),
那么线段MN的垂直平分线方程为y+2k1+2k2=-1k(x-4k21+2k2),
令y=0,得D(2k21+2k2,0),
|DH|=(4k21+2k2-2k21+2k2)2+(2k1+2k2)=2k4+k21+2k2,
|DH||MN|=2k4+k21+2k2⋅1+2k242(k2+1)=24k21+k2=241-11+k2.
∵k≠0,∴1+k2∈(1,+∞),则11+k2∈(0,1),
于是|DH||MN|∈(0,24).
【解析】本题主要考查利用定义求椭圆方程、直线与椭圆的位置关系.
(1)设P(x,y),由向量的坐标运算及椭圆定义可得P点轨迹方程;
(1)设出设直线斜率和M、N的坐标,得到直线的方程,与椭圆方程联立,利用韦达定理及弦长公式、中点坐标公式、两点间的距离公式化简整理,运用不等式的性质可得结论.