- 1.19 MB
- 2021-02-26 发布
§27.1.2 圆的对称性1
学习目标:经历探索圆的对称性及相关性质的过程.理解圆的对称性及相关知识.理解并掌握垂径定理.
学习重点:垂径定理及其应用.
学习难点:垂径定理及其应用.
学习方法:指导探索与自主探索相结合。
学习过程:
一、举例:
【例1】判断正误:
(1)直径是圆的对称轴.
(2)平分弦的直径垂直于弦.
【例2】若⊙O的半径为5,弦AB长为8,求拱高.
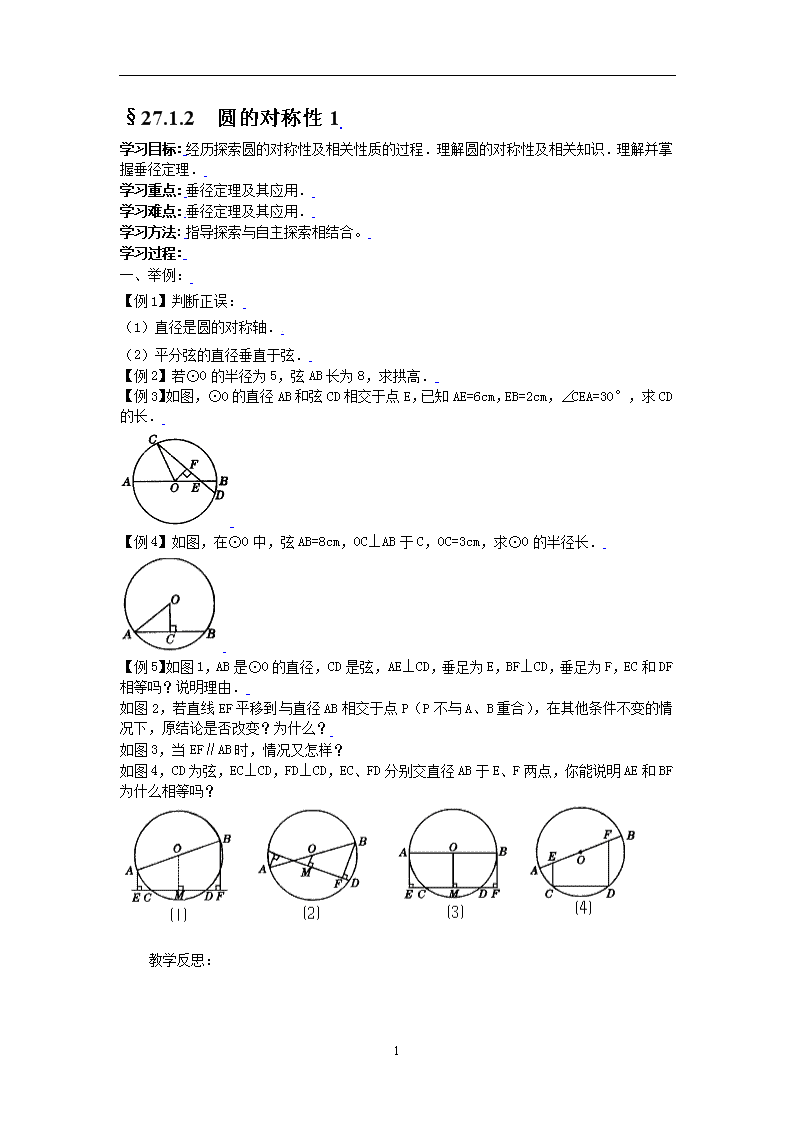
【例3】如图,⊙O的直径AB和弦CD相交于点E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD的长.
【例4】如图,在⊙O中,弦AB=8cm,OC⊥AB于C,OC=3cm,求⊙O的半径长.
【例5】如图1,AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,EC和DF相等吗?说明理由.
如图2,若直线EF平移到与直径AB相交于点P(P不与A、B重合),在其他条件不变的情况下,原结论是否改变?为什么?
如图3,当EF∥AB时,情况又怎样?
如图4,CD为弦,EC⊥CD,FD⊥CD,EC、FD分别交直径AB于E、F两点,你能说明AE和BF为什么相等吗?
教学反思:
2
§27.1.2 圆的对称性2
学习目标:
圆的旋转不变性,圆心角、弧、弦之间相等关系定理.
学习重点:
圆心角、弧、弦之间关系定理.
学习难点:
“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.
学习方法:
指导探索法.
学习过程:
一、例题讲解:
【例1】已知A,B是⊙O上的两点,∠AOB=1200,C是 的中点,试确定四边形OACB的形状,并说明理由.
【例2】如图,AB、CD、EF都是⊙O的直径,且∠1=∠2=∠3,弦AC、EB、DF是否相等?为什么?
【例3】如图,弦DC、FE的延长线交于⊙O外一点P,直线PAB经过圆心O,请你根据现有圆形,添加一个适当的条件: ,使∠1=∠2.
2
相关文档
- 八年级下册数学教案16-1 第1课时 2021-02-27 09:11:352页
- 六年级下册数学教案 正比例和反比2021-02-27 09:11:344页
- 三年级上册数学教案-6笔算乘法|人教2021-02-27 09:11:295页
- 六年级上册数学教案-7 百分数的意2021-02-27 09:11:259页
- 2020关于初中数学教师个人述职报告2021-02-27 09:10:3910页
- 2年级数学教案《 表内乘法 》说课2021-02-27 09:10:139页
- 数学(心得)之初探初中数学与现代信息2021-02-27 09:10:065页
- 六年级上册数学教案 黄金螺旋线 北2021-02-27 09:09:588页
- 六年级上册数学教案 -1 分数乘分数2021-02-27 09:09:523页
- 二年级上册数学教案-6整理与提高(数2021-02-27 09:09:503页