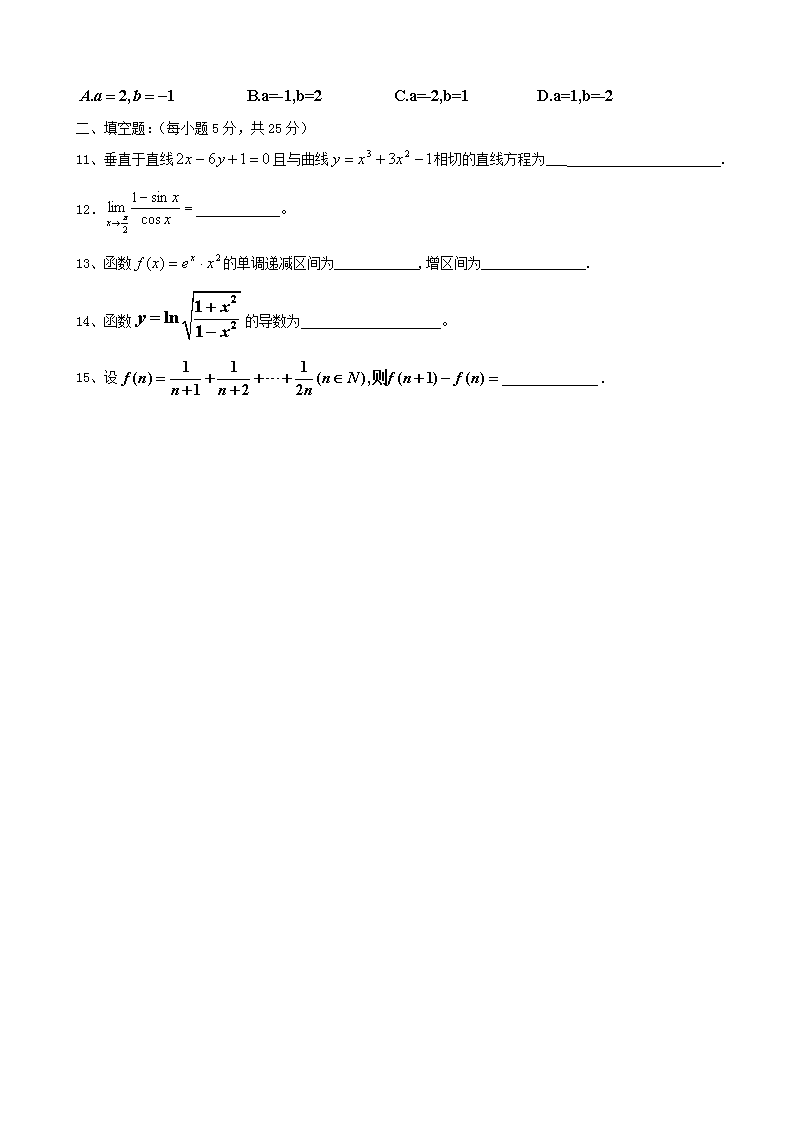湖南省蓝山二中2011-2012学年高二数学下学期期中考试试题 理 8页

高二理科数学试题 总分：150分 时量：120分钟 一、 选择题：（每小题5分，共50分）‎ ‎1、设已知,则与值分别为 ‎ ‎ ‎2、已知的导数为，则的值为 ‎ ‎ ‎3、函数,点是的 ‎ 连续不可导点 可导不连续点 可导且连续点 非极值点 ‎4、‎ ‎ ‎ ‎5、已知随机变量的概率密度函数为,则 ‎ A. B. C. D. ‎ ‎6、已知数列满足：‎ ‎ ‎ ‎7、已知在处有极值,则 ‎ ‎ ‎8、某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,适合的抽取样本的方法是 ‎ ‎ A. 简单的随机抽样 B. 系统抽样 ‎ C. 先从老年中排除一人,再用分层抽样 D.分层抽样 ‎9、已知，函数上是单调函数，则的取值范围是 ‎ ‎ ‎10、如果那么 一、 填空题：（每小题5分，共25分）‎ ‎11、垂直于直线且与曲线相切的直线方程为___ .‎ ‎12． 。‎ ‎13、函数的单调递减区间为____________,增区间为_______________.‎ ‎14、函数的导数为 。‎ ‎15、设 ‎蓝山二中2012年上高二期中考试 数 学 试 卷（第Ⅱ卷）‎ 总分：150分 时量：120分钟 一、 选择题：（50分）‎ 题号 ‎ 1‎ ‎2‎ ‎3‎ ‎ 4‎ ‎ 5‎ ‎ 6‎ ‎ 7‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ 答案 ‎ ‎ 二、 填空题：（25分）‎ ‎11、 ， 12、 ， 13、 ，‎ ‎14、 ， 15、 。‎ 三、解答题：（75分）‎ ‎16、甲、乙两人独立解出某一道数学题的概率相同，已知该题被甲或乙解出的概率为0.36. 求：（12分）‎ ‎ (1)甲独立解出该题的概率;‎ ‎ (2)解出该题的人数的数学期望. ‎ ‎17、如果函数在上单调递增,求的取值范围. (12)‎ ‎18、设函数（12分）‎ ‎（1）如果，点P为曲线上一个动点，求以P为切点的切线斜率取得最小值时的切线方程；‎ ‎（2）若时，恒成立，求的取值范围。‎ ‎19、已知数列{an}, {bn}, {cn}满足：a1=b1=1，且有(n=1, 2, 3,……)，cn=anbn, 试求 （12分）‎ ‎20、如下图，设P1，P2，P3，…，Pn，…是曲线y=上的点列，Q1，Q2，Q3， …，Qn，…是x轴正半轴上的点列，且△OQ1P1，△Q1Q2P2，…，△Qn－1QnPn，…都是正三角形，设它们的边长为a1，a2，…，an，…，求证：a1+a2+…+an=n（n+1）.（13分）‎ ‎ ‎ ‎ 21、(14分) 设函数的图像与y轴交点为,且曲线在点处的切线方程为,若函数在处取得极值为.(1)求函数解析式；(2)确定函数的单调递增区间；(3)证明：当 (14分)‎ ‎数学试卷参考答案：‎ 一、BCAAD ABCDD ‎16.解(1)设甲独立解出该题的概率为则乙独立解出该题的概率也为由题意得 ……(1分) ‎ 解得 …………………………………………………(5分)‎ 所以甲独立解出该题的概率是0.2.………………… …(6分)‎ ‎17、解：若则为一个二次函数，在上不是单调函数，故(2分)‎ ‎ 函数在上单调递增，………………… (5分)‎ ‎18、解：（1）设切线斜率为k,则。‎ 又。（6分）‎ ‎（1），（2）无解，由（3）解得，综上所述，错误！未找到引用源。‎ ‎19、解：由 ‎ ‎ ‎20、证明：（1）当n=1时，点P1是直线y=x与曲线y=的交点，‎ ‎∴可求出P1（，）.‎ ‎∴a1=|OP1|=.而×1×2=，命题成立.（6分）‎ ‎∴a1+a2+…+ak+a k+1=k（k+1）+（k+1）=（k+1）（k+2）.‎ ‎∴当n=k+1时，命题成立.‎ 由（1）（2）可知，命题对所有正整数都成立.（13分）‎ ‎21. 解(1)因为…………………………………………………(1分)‎ ‎,由题意得如下方程组 ‎.………………………………………(5分)‎ ‎(2) ,令,解得, (8分)‎ ‎ 所以函数的单调递增区间是. ………………………(9分)‎ ‎(3)令,解得,‎ 所以,原函数的减区间是, …………………………………………(10分)‎ ‎ ‎