- 485.00 KB
- 2021-06-18 发布
2016-2017学年河北省张家口市涿鹿中学高二(下)第一次月考数学试卷(文科)
一、单项选择题(60分,每小题5分)
1.抛物线y=﹣2x2的焦点坐标是( )
A. B.(﹣1,0) C. D.
2.函数f(x)在x=x0处导数存在,若p:f′(x0)=0;q:x=x0是f(x)的极值点,则p是q的( )
A.充分不必要条件 B.充要条件
C.必要不充条件 D.既非充分条件也非必要条件
3.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )
A. B. C. D.
4.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( )
A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,53
5.某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.67.7万元 C.65.5万元 D.72.0万元
6.函数的最大值为( )
A.e﹣1 B.e C.e2 D.
7.设F1、F2是椭圆E: +=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. B. C. D.
8.已知命题p:“∃x∈R,使”4x+2x+1﹣m=0”,若“¬p”为假命题,则实数m的取值范围是( )
A.(﹣1,+∞) B.(0,+∞) C.[0,+∞) D.[1,+∞)
9.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A. B.1 C. D.
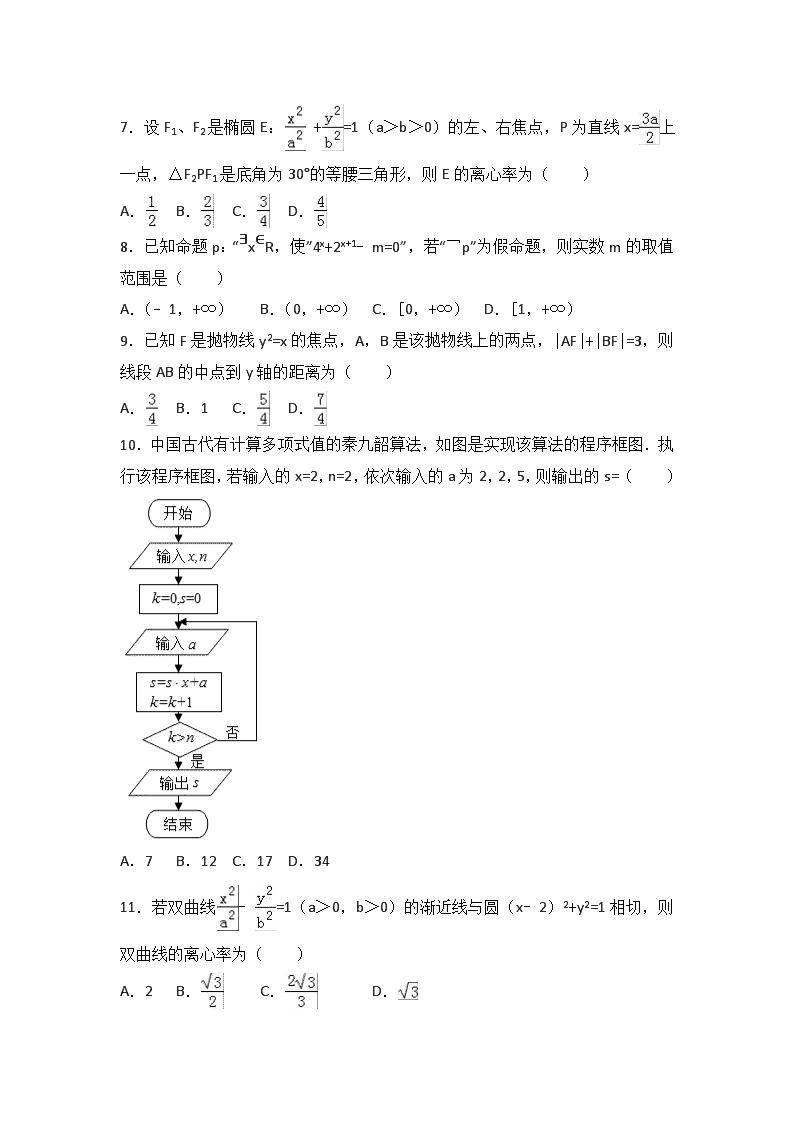
10.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7 B.12 C.17 D.34
11.若双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣2)2+y2=1相切,则双曲线的离心率为( )
A.2 B. C. D.
12.若函数f(x)=x﹣sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
A.[﹣1,1] B.[﹣1,] C.[﹣,] D.[﹣1,﹣]
二、填空题(20分,每小题5分)
13.用火柴棒摆“金鱼”,如图所示:按照上面的规律,第n个“金鱼”图需要火柴棒的根数为 .
14.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 .
15.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是 .
16.已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= .
三、解答题
17.点P是椭圆+=1上的一点,F1和F2是焦点,且∠F1PF2=30°,则△F1PF2的面积是 .
18.我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.
19.已知函数f(x)=ex(ax+b)﹣x2﹣4x,曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性,并求f(x)的极大值.
20.为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如表:
性别
是否需要志愿
男
女
需要
40
30
不需要
160
270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.附:
P(k2>k)
0.0
0.010
0.001
k
3.841
6.635
10.828
21.在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(Ⅰ)求;
(Ⅱ)除H以外,直线MH与C是否有其它公共点?说明理由.
22.已知函数f(x)=(x﹣2)ex+a(x﹣1)2.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点,求a的取值范围.
2016-2017学年河北省张家口市涿鹿中学高二(下)第一次月考数学试卷(文科)
参考答案与试题解析
一、单项选择题(60分,每小题5分)
1.抛物线y=﹣2x2的焦点坐标是( )
A. B.(﹣1,0) C. D.
【考点】抛物线的简单性质.
【分析】先把抛物线的方程化为标准形式,再利用抛物线 x2=﹣2p y 的焦点坐标为(0,﹣),求出物线y=﹣2x2的焦点坐标.
【解答】解:∵在抛物线y=﹣2x2,即 x2=﹣y,∴p=, =,
∴焦点坐标是 (0,﹣),
故选 D.
2.函数f(x)在x=x0处导数存在,若p:f′(x0)=0;q:x=x0是f(x)的极值点,则p是q的( )
A.充分不必要条件 B.充要条件
C.必要不充条件 D.既非充分条件也非必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用函数的极值的定义可以判断函数取得极值和导数值为0的关系.
【解答】解:根据函数极值的定义可知,函数x=x0为函数y=f(x)的极值点,f′(x)=0一定成立.
但当f′(x)=0时,函数不一定取得极值,
比如函数f(x)=x3.函数导数f′(x)=3x2,
当x=0时,f′(x)=0,但函数f(x)=x3单调递增,没有极值.
则p是q的必要不充分条件,
故选:C.
3.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )
A. B. C. D.
【考点】几何概型.
【分析】求出一名行人前25秒来到该路口遇到红灯,即可求出至少需要等待15秒才出现绿灯的概率.
【解答】解:∵红灯持续时间为40秒,至少需要等待15秒才出现绿灯,
∴一名行人前25秒来到该路口遇到红灯,
∴至少需要等待15秒才出现绿灯的概率为=.
故选:B.
4.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( )
A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,53
【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差.
【分析】直接利用茎叶图求出该样本的中位数、众数、极差,即可.
【解答】解:由题意可知茎叶图共有30个数值,所以中位数为第15和16个数的平均值: =46.
众数是45,极差为:68﹣12=56.
故选:A.
5.某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.67.7万元 C.65.5万元 D.72.0万元
【考点】线性回归方程.
【分析】根据表中所给的数据,广告费用x与销售额y(万元)的平均数,得到样本中心点,代入样本中心点求出的值,写出线性回归方程.将x=6代入回归直线方程,得y,可以预报广告费用为6万元时销售额.
【解答】解:由表中数据得: =3.5, ==42,
又回归方程=x+中的为9.4,
故=42﹣9.4×3.5=9.1,
∴=9.4x+9.1.
将x=6代入回归直线方程,得y=9.4×6+9.1=65.5(万元).
∴此模型预报广告费用为6万元时销售额为65.5(万元).
故选:C.
6.函数的最大值为( )
A.e﹣1 B.e C.e2 D.
【考点】函数在某点取得极值的条件.
【分析】
先找出导数值等于0的点,再确定在此点的左侧及右侧导数值的符号,确定此点是函数的极大值点还是极小值点,
从而求出极值.
【解答】解:令,
当x>e时,y′<0;
当x<e时,y′>0,,
在定义域内只有一个极值,
所以,
故答案选 A.
7.设F1、F2是椭圆E: +=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. B. C. D.
【考点】椭圆的简单性质.
【分析】利用△F2PF1是底角为30°的等腰三角形,可得|PF2|=|F2F1|,根据P为直线x=上一点,可建立方程,由此可求椭圆的离心率.
【解答】解:∵△F2PF1是底角为30°的等腰三角形,
∴|PF2|=|F2F1|
∵P为直线x=上一点
∴
∴
故选C.
8.已知命题p:“∃x∈R,使”4x+2x+1﹣m=0”,若“¬p”为假命题,则实数m的取值范围是( )
A.(﹣1,+∞) B.(0,+∞) C.[0,+∞) D.[1,+∞)
【考点】复合命题的真假.
【分析】若¬P是假命题,则P是真命题,根据特称命题的性质进行求解即可.
【解答】解:若¬P是假命题,则P是真命题,
即∃x∈R,使4x+2x+1﹣m=0,
则m=4x+2x+1=4x+2•2x=(2x+1)2﹣1,
∵2x>0,
∴(2x+1)2﹣1>0,
即m>0,
故选:B.
9.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A. B.1 C. D.
【考点】抛物线的简单性质.
【分析】根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,求出线段AB的中点到y轴的距离.
【解答】解:∵F是抛物线y2=x的焦点,
F()准线方程x=,
设A(x1,y1),B(x2,y2),
根据抛物线的定义抛物线上的点到焦点的距离等于到准线的距离|AF|=,|BF|=,
∴|AF|+|BF|==3
解得,
∴线段AB的中点横坐标为,
∴线段AB的中点到y轴的距离为.
故选C.
10.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7 B.12 C.17 D.34
【考点】程序框图.
【分析】
根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.
【解答】解:∵输入的x=2,n=2,
当输入的a为2时,S=2,k=1,不满足退出循环的条件;
当再次输入的a为2时,S=6,k=2,不满足退出循环的条件;
当输入的a为5时,S=17,k=3,满足退出循环的条件;
故输出的S值为17,
故选:C
11.若双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣2)2+y2=1相切,则双曲线的离心率为( )
A.2 B. C. D.
【考点】双曲线的简单性质.
【分析】求出双曲线的渐近线方程,圆的圆心和半径,再由直线和圆相切的条件可得a=b,再由a,b,c的关系和离心率公式计算即可得到.
【解答】解:双曲线﹣=1(a>0,b>0)的渐近线方程为
y=x,
圆(x﹣2)2+y2=1的圆心为(2,0),半径为1,
则由圆心到直线的距离为1,可得
=1,
解得a=b,
c===a,
则有e==.
故选C.
12.若函数f(x)=x﹣sin2x+asinx在(﹣∞,+∞
)单调递增,则a的取值范围是( )
A.[﹣1,1] B.[﹣1,] C.[﹣,] D.[﹣1,﹣]
【考点】利用导数研究函数的单调性.
【分析】求出f(x)的导数,由题意可得f′(x)≥0恒成立,设t=cosx(﹣1≤t≤1),即有5﹣4t2+3at≥0,对t讨论,分t=0,0<t≤1,﹣1≤t<0,分离参数,运用函数的单调性可得最值,解不等式即可得到所求范围.
【解答】解:函数f(x)=x﹣sin2x+asinx的导数为f′(x)=1﹣cos2x+acosx,
由题意可得f′(x)≥0恒成立,
即为1﹣cos2x+acosx≥0,
即有﹣cos2x+acosx≥0,
设t=cosx(﹣1≤t≤1),即有5﹣4t2+3at≥0,
当t=0时,不等式显然成立;
当0<t≤1时,3a≥4t﹣,
由4t﹣在(0,1]递增,可得t=1时,取得最大值﹣1,
可得3a≥﹣1,即a≥﹣;
当﹣1≤t<0时,3a≤4t﹣,
由4t﹣在[﹣1,0)递增,可得t=﹣1时,取得最小值1,
可得3a≤1,即a≤.
综上可得a的范围是[﹣,].
故选:C.
二、填空题(20分,每小题5分)
13.用火柴棒摆“金鱼”,如图所示:按照上面的规律,第n个“金鱼”图需要火柴棒的根数为
6n+2 .
【考点】归纳推理.
【分析】观察给出的3个例图,注意火柴棒根数的变化是图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,而图①的火柴棒的根数为2+6.
【解答】解:由题意知:图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,而图①的火柴棒的根数为2+6,
∴第n条小鱼需要(2+6n)根,
故答案为:6n+2.
14.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 0.1 .
【考点】极差、方差与标准差.
【分析】先求出数据4.7,4.8,5.1,5.4,5.5的平均数,由此能求出该组数据的方差.
【解答】解:∵数据4.7,4.8,5.1,5.4,5.5的平均数为:
=(4.7+4.8+5.1+5.4+5.5)=5.1,
∴该组数据的方差:
S2= [(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1.
故答案为:0.1.
15.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是 x+2y﹣8=0 .
【考点】直线与圆锥曲线的综合问题.
【分析】若设弦的端点为A(x1,y1)、B(x2,y2),代入椭圆方程得9x12+36y12=36×9①,9x22+36y22=36×9②;作差①﹣②,并由中点坐标公式,可得直线斜率k,从而求出弦所在的直线方程.
【解答】解:设弦的端点为A(x1,y1)、B(x2,y2),
代入椭圆方程,得
9x12+36y12=36×9①,
9x22+36y22=36×9②;
①﹣②得
9(x1+x2)(x1﹣x2)+36(y1+y2)(y1﹣y2)=0;
由中点坐标=4, =2,
代入上式,得
36(x1﹣x2)+72(y1﹣y2)=0,
∴直线斜率为k==﹣,
所求弦的直线方程为:y﹣2=﹣(x﹣4),
即x+2y﹣8=0.
故答案为:x+2y﹣8=0.
16.已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= 8 .
【考点】利用导数研究曲线上某点切线方程.
【分析】求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.
【解答】解:y=x+lnx的导数为y′=1+,
曲线y=x+lnx在x=1处的切线斜率为k=2,
则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2,即y=2x﹣1.
由于切线与曲线y=ax2+(a+2)x+1相切,
故y=ax2+(a+2)x+1可联立y=2x﹣1,
得ax2+ax+2=0,
又a≠0,两线相切有一切点,
所以有△=a2﹣8a=0,
解得a=8.
故答案为:8.
三、解答题
17.点P是椭圆+=1上的一点,F1和F2是焦点,且∠F1PF2=30°,则△F1PF2的面积是 8﹣4 .
【考点】椭圆的简单性质.
【分析】方法一:由椭圆的定义可知:|PF1|+|PF2|=2a=2,由余弦定理:|PF1|2+|PF2|2﹣2|PF1|⋅|PF2|⋅cos30∘=|F1F2|2=(2c)2=4,代入即可求得:|PF1|⋅|PF2|,根据三角形的面积公式可知:S=|PF1|⋅|PF2|⋅sin30°,即可求得△F1PF2的面积.
【解答】解:方法一:由题意可知:椭圆+=1焦点在y轴上,a=,b=2,c=1,
又∵P在椭圆上,则|PF1|+|PF2|=2a=2,
由余弦定理得:|PF1|2+|PF2|2﹣2|PF1|⋅|PF2|⋅cos30∘=|F1F2|2=(2c)2=4
解得:|PF1|⋅|PF2|=16(2﹣),
∴△PF1F2的面积S=|PF1|⋅|PF2|⋅sin30°=8﹣4,
故答案为:8﹣4.
方法二:由题意可知:椭圆+=1焦点在y轴上,a=,b=2,c=1,
由焦点三角形的面积公式可知:△F1PF2的面积S=b2•
=4×=8﹣4,
故答案为:8﹣4.
18.我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.
【考点】众数、中位数、平均数;频率分布直方图.
【分析】(I)先根据频率分布直方图中的频率等于纵坐标乘以组距求出9个矩形的面积即频率,再根据直方图的总频率为1求出a的值;
(II)根据已知中的频率分布直方图先求出月均用水量不低于3吨的频率,结合样本容量为30万,进而得解.
(Ⅲ)根据频率分布直方图,求出使直方图中左右两边频率相等对应的横坐标的值.
【解答】解:(I)∵1=(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5,
整理可得:2=1.4+2a,
∴解得:a=0.3.
(II)估计全市居民中月均用水量不低于3吨的人数为3.6万,理由如下:
由已知中的频率分布直方图可得月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12,
又样本容量为30万,
则样本中月均用水量不低于3吨的户数为30×0.12=3.6万.
(Ⅲ)根据频率分布直方图,得;
0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5=0.48<0.5,
0.48+0.5×0.52=0.74>0.5,
∴中位数应在(2,2.5]组内,设出未知数x,
令0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5+0.52×x=0.5,
解得x=0.04;
∴中位数是2+0.04=2.04.
19.已知函数f(x)=ex(ax+b)﹣x2﹣4x,曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性,并求f(x)的极大值.
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数研究函数的极值.
【分析】(Ⅰ)求导函数,利用导数的几何意义及曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4,建立方程,即可求得a,b的值;
(Ⅱ)利用导数的正负,可得f(x)的单调性,从而可求f(x)的极大值.
【解答】解:(Ⅰ)∵f(x)=ex(ax+b)﹣x2﹣4x,
∴f′(x)=ex(ax+a+b)﹣2x﹣4,
∵曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4
∴f(0)=4,f′(0)=4
∴b=4,a+b=8
∴a=4,b=4;
(Ⅱ)由(Ⅰ)知,f(x)=4ex(x+1)﹣x2﹣4x,f′(x)=4ex(x+2)﹣2x﹣4=4(x+2)(ex﹣),
令f′(x)=0,得x=﹣ln2或x=﹣2
∴x∈(﹣∞,﹣2)或(﹣ln2,+∞)时,f′(x)>0;x∈(﹣2,﹣ln2)时,f′(x)<0
∴f(x)的单调增区间是(﹣∞,﹣2),(﹣ln2,+∞),单调减区间是(﹣2,﹣ln2)
当x=﹣2时,函数f(x)取得极大值,极大值为f(﹣2)=4(1﹣e﹣2).
20.为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如表:
性别
是否需要志愿
男
女
需要
40
30
不需要
160
270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
0.0
0.010
0.001
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.附:
P(k2>k)
k
3.841
6.635
10.828
【考点】简单随机抽样;独立性检验.
【分析】(1)由列联表可知调查的500位老年人中有40+30=70位需要志愿者提供帮助,两个数据求比值得到该地区老年人中需要帮助的老年人的比例的估算值.
(2)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,看出有多大把握说该地区的老年人是否需要帮助与性别有关.
(3)从样本数据老年人中需要帮助的比例有明显差异,调查时,可以先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.
【解答】解:(1)∵调查的500位老年人中有40+30=70位需要志愿者提供帮助,
∴该地区老年人中需要帮助的老年人的比例的估算值为.
(2)根据列联表所给的数据,代入随机变量的观测值公式,
.
∵9.967>6.635,
∴有99%的把握认为该地区的老年人是否需要帮助与性别有关.
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.
21.在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(Ⅰ)求;
(Ⅱ)除H以外,直线MH与C是否有其它公共点?说明理由.
【考点】抛物线的简单性质.
【分析】(Ⅰ)求出P,N,H的坐标,利用=,求;
(Ⅱ)直线MH的方程为y=x+t,与抛物线方程联立,消去x可得y2﹣4ty+4t2=0,利用判别式可得结论.
【解答】解:(Ⅰ)将直线l与抛物线方程联立,解得P(,t),
∵M关于点P的对称点为N,
∴=, =t,
∴N(,t),
∴ON的方程为y=x,
与抛物线方程联立,解得H(,2t)
∴==2;
(Ⅱ)由(Ⅰ)知kMH=,
∴直线MH的方程为y=x+t,与抛物线方程联立,消去x可得y2﹣4ty+4t2=0,
∴△=16t2﹣4×4t2=0,
∴直线MH与C除点H外没有其它公共点.
22.已知函数f(x)=(x﹣2)ex+a(x﹣1)2.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点,求a的取值范围.
【考点】利用导数研究函数的单调性;函数零点的判定定理.
【分析】(Ⅰ)求出f(x)的导数,讨论当a≥0时,a<﹣时,a=﹣时,﹣<a<0,由导数大于0,可得增区间;由导数小于0,可得减区间;
(Ⅱ)由(Ⅰ)的单调区间,对a讨论,结合单调性和函数值的变化特点,即可得到所求范围.
【解答】解:(Ⅰ)由f(x)=(x﹣2)ex+a(x﹣1)2,
可得f′(x)=(x﹣1)ex+2a(x﹣1)=(x﹣1)(ex+2a),
①当a≥0时,由f′(x)>0,可得x>1;由f′(x)<0,可得x<1,
即有f(x)在(﹣∞,1)递减;在(1,+∞)递增;
②当a<0时,若a=﹣,则f′(x)≥0恒成立,即有f(x)在R上递增;
若a<﹣时,由f′(x)>0,可得x<1或x>ln(﹣2a);
由f′(x)<0,可得1<x<ln(﹣2a).
即有f(x)在(﹣∞,1),(ln(﹣2a),+∞)递增;
在(1,ln(﹣2a))递减;
若﹣<a<0,由f′(x)>0,可得x<ln(﹣2a)或x>1;
由f′(x)<0,可得ln(﹣2a)<x<1.
即有f(x)在(﹣∞,ln(﹣2a)),(1,+∞)递增;
在(ln(﹣2a),1)递减;
(Ⅱ)
①由(Ⅰ)可得当a>0时,f(x)在(﹣∞,1)递减;在(1,+∞)递增,
且f(1)=﹣e<0,x→+∞,f(x)→+∞;x→﹣∞,f(x)→+∞.f(x)有两个零点;
②当a=0时,f(x)=(x﹣2)ex,所以f(x)只有一个零点x=2;
③当a<0时,
若a<﹣时,f(x)在(1,ln(﹣2a))递减,在(﹣∞,1),(ln(﹣2a),+∞)递增,
又当x≤1时,f(x)<0,所以f(x)不存在两个零点;
当a≥﹣时,f(x)在(1,+∞)单调递增,又x≤1时,f(x)<0,所以f(x)不存在两个零点.
综上可得,f(x)有两个零点时,a的取值范围为(0,+∞).