- 312.01 KB
- 2021-06-17 发布
全*品*高*考*网, 用后离不了!2016-2017学年安徽省马鞍山二十二中高三(上)开学数学试卷 (文科)
一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( )
A.{1,3} B.{3,5} C.{5,7} D.{1,7}
2.函数f(x)=+的定义域为( )
A.{x|x<1} B.{x|0<x<1} C.{x|0<x≤1} D.{x|x>1}
3.已知命题p:∀x∈R,sinx≤1,则¬p为( )
A.∃x∈R,sinx≥1 B.∀x∈R,sinx≥1 C.∃x∈R,sinx>1 D.∀x∈R,sinx>1
4.已知向量,满足+=(1,﹣3),﹣=(3,7),•=( )
A.﹣12 B.﹣20 C.12 D.20
5.△ABC的内角A、B、C的对边分别为a、b、c.已知a=,c=2,cosA=,则b=( )
A. B. C.2 D.3
6.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
A.96 B. C. D.
7.直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=1”是“|AB|=”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.在区间[﹣5,4]上随机取一个数x,使不等式>1成立的概率为( )
A. B. C. D.
9.若某程序框图如图所示,则该程序运行后输出的值是( )
A.2 B.3 C.4 D.5
10.将函数f(x)=sin(2x+)的图象向左平移φ(φ>0)个单位后,得到的函数图象关于y轴对称,则φ的最小值为( )
A.π B.π C. D.
11.已知实数x,y满足不等式组,则z=x+2y的最小值为( )
A.﹣4 B.5 C.4 D.无最小值
12.设函数g(x)=x2﹣2(x∈R),f(x)=,则f(x)的值域是( )
A.[﹣,0]∪(1,+∞) B.[0,+∞) C.[,+∞) D.[﹣,0]∪(2,+∞)
二、填空题:本大题共4小题,每小题5分
13.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为 .
14.已知cos(π+x)=,x∈(π,2π),则tanx= .
15.等比数列{an}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5= .
16.已知圆x2+y2﹣2x﹣4y+3=0关于直线ax+by﹣3=0(a>0,b>0)对称,则+的最小值为 .
三.解答题:解答应写出文字说明,证明过程或演算步骤.
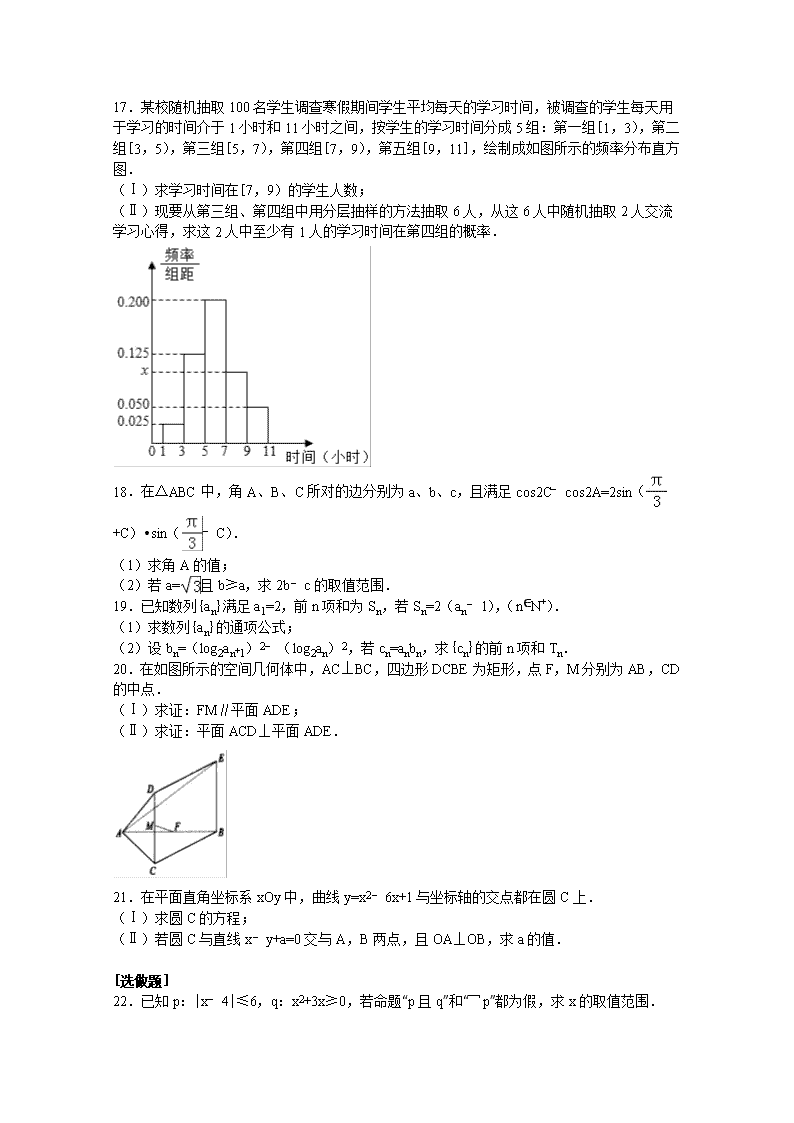
17.某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.
(Ⅰ)求学习时间在[7,9)的学生人数;
(Ⅱ)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人的学习时间在第四组的概率.
18.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C﹣cos2A=2sin(+C)•sin(﹣C).
(1)求角A的值;
(2)若a=且b≥a,求2b﹣c的取值范围.
19.已知数列{an}满足a1=2,前n项和为Sn,若Sn=2(an﹣1),(n∈N+).
(1)求数列{an}的通项公式;
(2)设bn=(log2an+1)2﹣(log2an)2,若cn=anbn,求{cn}的前n项和Tn.
20.在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.
(Ⅰ)求证:FM∥平面ADE;
(Ⅱ)求证:平面ACD⊥平面ADE.
21.在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交与A,B两点,且OA⊥OB,求a的值.
[选做题]
22.已知p:|x﹣4|≤6,q:x2+3x≥0,若命题“p且q”和“¬p”都为假,求x的取值范围.
[选做题]
23.已知F1、F2为椭圆+=1(a>b>0)的左、右焦点,过F2做椭圆的弦AB.
(Ⅰ) 求证:△F1AB的周长是常数;
(Ⅱ) 若:△F1AB的周长为16,且|AF1|、|F1F2|、|AF2|成等差数列,求椭圆方程.
[选做题]
24.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a、b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(﹣∞,﹣1)上的最大值.
2016-2017学年安徽省马鞍山二十二中高三(上)开学数学试卷 (文科)
参考答案与试题解析
一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( )
A.{1,3} B.{3,5} C.{5,7} D.{1,7}
【考点】交集及其运算.
【分析】直接利用交集的运算法则化简求解即可.
【解答】解:集合A={1,3,5,7},B={x|2≤x≤5},
则A∩B={3,5}.
故选:B.
2.函数f(x)=+的定义域为( )
A.{x|x<1} B.{x|0<x<1} C.{x|0<x≤1} D.{x|x>1}
【考点】函数的定义域及其求法;对数函数的定义域.
【分析】根据函数成立的条件即可求函数的定义域.
【解答】解:要使函数有意义,则,
即,得0<x<1,
即函数的定义域为{x|0<x<1},
故选:B
3.已知命题p:∀x∈R,sinx≤1,则¬p为( )
A.∃x∈R,sinx≥1 B.∀x∈R,sinx≥1 C.∃x∈R,sinx>1 D.∀x∈R,sinx>1
【考点】命题的否定.
【分析】根据全称命题的否定是特称命题可得命题的否定为∃x∈R,使得sinx>1
【解答】解:根据全称命题的否定是特称命题可得,
命题p:∀x∈R,sinx≤1,的否定是∃x∈R,使得sinx>1
故选:C
4.已知向量,满足+=(1,﹣3),﹣=(3,7),•=( )
A.﹣12 B.﹣20 C.12 D.20
【考点】平面向量数量积的运算.
【分析】求出两向量的坐标,代入数量积的坐标运算即可.
【解答】解:∵=(4,4),
∴,∴=(﹣1,﹣5).
∴=2×(﹣1)﹣2×5=﹣12.
故选A.
5.△ABC的内角A、B、C的对边分别为a、b、c.已知a=,c=2,cosA=,则b=( )
A. B. C.2 D.3
【考点】余弦定理.
【分析】由余弦定理可得cosA=,利用已知整理可得3b2﹣8b﹣3=0,从而解得b的值.
【解答】解:∵a=,c=2,cosA=,
∴由余弦定理可得:cosA===,整理可得:3b2﹣8b﹣3=0,
∴解得:b=3或﹣(舍去).
故选:D.
6.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
A.96 B. C. D.
【考点】由三视图求面积、体积.
【分析】几何体为边长为4的正方体挖去一个圆锥得到的.
【解答】解:由三视图可知几何体为边长为4的正方体挖去一个圆锥得到的,圆锥的底面半径为2,高为2,∴圆锥的母线长为2.
∴几何体的平面部分面积为6×42﹣π×22=96﹣4π.
圆锥的侧面积为=4.
∴几何体的表面积为96﹣4π+4.
故选:C.
7.直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=1”是“|AB|=”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分条件和必要条件的定义结合直线和圆相交的弦长公式进行判断即可.
【解答】解:∵直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,
∴圆心到直线的距离d=,
则|AB|=2=2,
当k=1时,|AB|=,即充分性成立,
若|AB|=,则,
即k2=1,解得k=1或k=﹣1,即必要性不成立,
故“k=1”是“|AB|=”的充分不必要条件,
故选:A
8.在区间[﹣5,4]上随机取一个数x,使不等式>1成立的概率为( )
A. B. C. D.
【考点】几何概型.
【分析】由题意,本题符合几何概型,只要求出区间的长度以及使不等式成立的x的范围区间长度,利用几何概型公式即可求得结果.
【解答】解:不等式>1可化为﹣1>0,
即<0,
解得﹣2<x<1;
又区间[﹣5,4]的长度为9,
使得>1成立的x的范围是(﹣2,1),区间长度为3,
由几何概型公式可得
使得>1成立的概率为P==.
故选:D.
9.若某程序框图如图所示,则该程序运行后输出的值是( )
A.2 B.3 C.4 D.5
【考点】程序框图.
【分析】根据所给数值判定是否满足判断框中的条件,然后执行循环语句,一旦不满足条件就退出循环,执行语句输出i,从而到结论.
【解答】解:当输入的值为n=6时,
n不满足上判断框中的条件,n=3,i=2,
n不满足下判断框中的条件,n=3,
n满足上判断框中的条件,n=4,i=3,
n不满足下判断框中的条件,n=4,
n不满足上判断框中的条件,n=2,i=4,
n满足下面一个判断框中的条件,退出循环,
即输出的结果为i=4,
故选C.
10.将函数f(x)=sin(2x+)的图象向左平移φ(φ>0)个单位后,得到的函数图象关于y轴对称,则φ的最小值为( )
A.π B.π C. D.
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
【解答】解:将函数f(x)=sin(2x+)的图象向左平移φ(φ>0)个单位后,
可得函数y=sin[2(x+φ)+]=sin(2x+2φ+)的图象.
再根据得到的函数图象关于y轴对称,可得2φ+的最小正值为,∴φ=,
故选:D.
11.已知实数x,y满足不等式组,则z=x+2y的最小值为( )
A.﹣4 B.5 C.4 D.无最小值
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用z的几何意义,即可求出z的最大值.
【解答】解:作出不等式组对应的平面区域如图:
设z=x+2y,则y=﹣x+
平移此直线,由图象可知当直线y=﹣x+经过A时,直线在y轴的截距最小,得到z最小,由得到A(2,1),
所以z=x+2y的最小值为2+2×1=4;
故选C.
12.设函数g(x)=x2﹣2(x∈R),f(x)=,则f(x)的值域是( )
A.[﹣,0]∪(1,+∞) B.[0,+∞) C.[,+∞) D.[﹣,0]∪(2,+∞)
【考点】分段函数的应用.
【分析】当x<g(x)时,x>2 或x<﹣1,f(x)=g(x)+x+4=x2﹣2+x+4=x2+x+2=(x+0.5)2+1.75,其值域为:(2,+∞).当x≥g(x)时,﹣1≤x≤2,f(x)=g(x)﹣x=x2﹣2﹣x=(x﹣0.5)2﹣2.25,其值域为:[﹣2.25,0].由此能得到函数值域.
【解答】解:当x<g(x),即x<x2﹣2,(x﹣2)(x+1)>0时,x>2 或x<﹣1,
f(x)=g(x)+x+4=x2﹣2+x+4=x2+x+2=(x+0.5)2+1.75,
∴其最小值为f(﹣1)=2,其最大值为+∞,
因此这个区间的值域为:(2,+∞).
当x≥g(x)时,﹣1≤x≤2,
f(x)=g(x)﹣x=x2﹣2﹣x=(x﹣0.5)2﹣2.25
其最小值为f(0.5)=﹣2.25,其最大值为f(2)=0
因此这区间的值域为:[﹣2.25,0].
综合得:函数值域为:[﹣2.25,0]U(2,+∞),
故选D.
二、填空题:本大题共4小题,每小题5分
13.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为 2x﹣y﹣1=0 .
【考点】待定系数法求直线方程.
【分析】根据﹣1≤x≤3,求出线段的端点坐标,在中点坐标,两直线的斜率乘积等于﹣1,即可得到方程.
【解答】解:由x﹣2y+1=0(﹣1≤x≤3),线段的端点坐标分别为(﹣1,0),(3,2),则中点坐标为()
∵方程余线段垂直,两直线的斜率乘积等于﹣1,设垂直平分线方程斜率为k,则k×=﹣1,
解得:k=2,
所以:垂直平分线方程为:2x﹣y﹣1=0
故答案为:2x﹣y﹣1=0.
14.已知cos(π+x)=,x∈(π,2π),则tanx= .
【考点】同角三角函数基本关系的运用.
【分析】先把已知的等式利用诱导公式化简,得到cosx的值,然后根据x的范围,利用同角三角函数间的基本关系求出sinx的值,进而求出tanx的值.
【解答】解:∵cos(π+x)=﹣cosx=,
∴cosx=﹣,又x∈(π,2π),
∴sinx=﹣=﹣,
则tanx===.
故答案为:
15.等比数列{an}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5= 5 .
【考点】等比数列的性质;对数的运算性质;等比数列的前n项和.
【分析】可先由等比数列的性质求出a3=2,再根据性质化简log2a1+log2a2+log2a3+log2a4+log2a5=5log2a3,代入即可求出答案.
【解答】解:log2a1+log2a2+log2a3+log2a4+log2a5=log2a1a2a3a4a5=log2a35=5log2a3.
又等比数列{an}中,a1a5=4,即a3=2.
故5log2a3=5log22=5.
故选为:5.
16.已知圆x2+y2﹣2x﹣4y+3=0关于直线ax+by﹣3=0(a>0,b>0)对称,则+的最小值为 2+ .
【考点】直线与圆的位置关系;基本不等式.
【分析】求出圆的圆心代入直线方程,然后利用基本不等式求解最值即可.
【解答】解:∵圆x2+y2﹣2x﹣4y+3=0⇔(x﹣1)2+(y﹣2)2=2,
圆x2+y2﹣2x﹣4y+3=0关于直线ax+by﹣3=0(a>0,b>0)对称,
∴该直线经过圆心(1,2),
把圆心(1,2)代入直线ax+by﹣3=0(a>0,b>0),得:a+2b﹣3=0
∴a+2b=3,a>0,b>0
∴+=×(+)(a+b)=(1+4++)≥(5+2)=3
当且仅当=,即a=b=1时取得最小值为3
故答案为:3.
三.解答题:解答应写出文字说明,证明过程或演算步骤.
17.某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.
(Ⅰ)求学习时间在[7,9)的学生人数;
(Ⅱ)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人的学习时间在第四组的概率.
【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图.
【分析】(Ⅰ)由频率分布图求出x=0.100,由此能求出学习时间在[7,9)的学生人数.
(Ⅱ)第三组的学生人数为40人,利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:第三组的人数为4人,第四组的人数为2人,由此能求出这2人中至少有1人的学习时间在第四组的概率.
【解答】解:(Ⅰ)由频率分布图得:0.025×2+0.125×2+0.200×2+2x+0.050×2=1,
解得x=0.100.
∴学习时间在[7,9)的学生人数为0.010×2×100=20人.
(Ⅱ)第三组的学生人数为0.200×2×100=40人,
第三、四组共有20+40=60人,
利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:
第三组的人数为6×=4人,第四组的人数为6×=2人,
则从这6人中抽2人,基本事件总数n==15,
其中2人学习时间都不在第四组的基本事件个数m==6,
∴这2人中至少有1人的学习时间在第四组的概率:
p=1﹣=.
18.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C﹣cos2A=2sin(+C)•sin(﹣C).
(1)求角A的值;
(2)若a=且b≥a,求2b﹣c的取值范围.
【考点】三角函数中的恒等变换应用;正弦定理.
【分析】(1)利用三角函数恒等变换的应用化简已知可解得:cos2A=﹣,结合2A∈(0,2π),可得A的值.
(2)由b≥a,由(1)可得:A=,又a=,由正弦定理可得: =2,从而利用三角函数恒等变换的应用可得2b﹣c=2sin(B﹣),结合范围B﹣∈[,),可得2b﹣c取值范围.
【解答】解:(1)∵cos2C﹣cos2A=2sin(+C)•sin(﹣C)
=2(cosC+sinC)(cosC﹣sinC)
=cos2C﹣sin2C
=•﹣•
=+cos2C,
∴﹣cos2A=,解得:cos2A=﹣.
∵A∈(0,π),2A∈(0,2π),
∴当2A=时,解得:A=,
当2A=时,解得:A=.
(2)∵b≥a,∴A为锐角,由(1)可得:A=,
又∵a=,
∴由正弦定理可得: ==2,
∴2b﹣c=2(2sinB﹣sinC)=4sinB﹣2sin(﹣B)=4sinB﹣(cosB+sinB)=3sinB﹣cosB=2sin(B﹣),
∵B∈[,),B﹣∈[,),可得sin(B﹣)∈[,1),
∴2b﹣c=2sin(B﹣)∈[,2).
19.已知数列{an}满足a1=2,前n项和为Sn,若Sn=2(an﹣1),(n∈N+).
(1)求数列{an}的通项公式;
(2)设bn=(log2an+1)2﹣(log2an)2,若cn=anbn,求{cn}的前n项和Tn.
【考点】数列递推式;数列的求和.
【分析】(1)由题意和当n≥2时an=Sn﹣Sn﹣1进行化简,得到数列的递推公式,由等比数列的定义判断出数列{an}是等比数列,由等比数列的通项公式求出{an}的通项公式;
(2)由(1)和对数的运算化简bn=(log2an+1)2﹣(log2an)2,代入cn=anbn化简后,利用错位相减法和等比数列的前n项和公式求Tn.
【解答】解:(1)∵Sn=2(an﹣1),
∴当n≥2时,an=Sn﹣Sn﹣1=2(an﹣1)﹣2(an﹣1﹣1)
=2(an﹣an﹣1),则an=2an﹣1,
又a1=2,则数列{an}是以2为首项、公比的等比数列,
∴=2n;
(2)由(1)得,bn=(log2an+1)2﹣(log2an)2
=(n+1)2﹣n2=2n+1,
∴cn=anbn=(2n+1)•2n,
∴Tn=3×2+5×22+…+(2n+1)×2n,①
则2Tn=3×22+5×23+…+(2n+1)×2n+1,②
①﹣②得:﹣Tn=6+2(22+23+…+2n)﹣(2n+1)•2n+1
=6+2×﹣(2n+1)•2n+1=(﹣2n+1)•2n+1﹣2,
∴Tn=(2n﹣1)•2n+1+2.
20.在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.
(Ⅰ)求证:FM∥平面ADE;
(Ⅱ)求证:平面ACD⊥平面ADE.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【分析】(Ⅰ)取BE中点N,连结MN、FN,推导出平面FMN∥平面ADE,由此能证明FM∥平面ADE.
(Ⅱ)推导出BC⊥DC,BC⊥平面ACD,从而DE⊥平面ACD,由此能证明平面ACD⊥平面ADE.
【解答】证明:(Ⅰ)取BE中点N,连结MN、FN,
∵F、M、N分别为AB、CD、BE的中点,
∴MN∥DE,FN∥AE,
又∵AE,DE⊂平面ADE,FN、MN⊄平面ADE,
∴MN∥平面ADE,FN∥ADE,
MN∩FN=N,∴平面FMN∥平面ADE,
FM⊂平面FMN,∴FM∥平面ADE.
(Ⅱ)∵四边形DCBE为矩形,∴BC⊥DC,
又AC⊥BC,AC∩DC=C,∴BC⊥平面ACD,
又∵BC∥DE,∴DE⊥平面ACD,
∵DE⊂平面ADE,∴平面ACD⊥平面ADE.
21.在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交与A,B两点,且OA⊥OB,求a的值.
【考点】圆的标准方程;直线与圆相交的性质.
【分析】(Ⅰ)法一:写出曲线与坐标轴的交点坐标,利用圆心的几何特征设出圆心坐标,构造关于圆心坐标的方程,通过解方程确定出圆心坐标,进而算出半径,写出圆的方程;
法二:可设出圆的一般式方程,利用曲线与方程的对应关系,根据同一性直接求出参数,
(Ⅱ)利用设而不求思想设出圆C与直线x﹣y+a=0的交点A,B坐标,通过OA⊥OB建立坐标之间的关系,结合韦达定理寻找关于a的方程,通过解方程确定出a的值.
【解答】解:(Ⅰ)法一:曲线y=x2﹣6x+1与y轴的交点为(0,1),与x轴的交点为(3+2,0),(3﹣2,0).可知圆心在直线x=3上,故可设该圆的圆心C为(3,t),则有32+(t﹣1)2=(2)2+t2,解得t=1,故圆C的半径为,所以圆C的方程为(x﹣3)2+(y﹣1)2=9.
法二:圆x2+y2+Dx+Ey+F=0
x=0,y=1有1+E+F=0
y=0,x2 ﹣6x+1=0与x2+Dx+F=0是同一方程,故有D=﹣6,F=1,E=﹣2,
即圆方程为x2+y2﹣6x﹣2y+1=0
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足方程组
,消去y,得到方程2x2+(2a﹣8)x+a2﹣2a+1=0,由已知可得判别式△=56﹣16a﹣4a2>0.
在此条件下利用根与系数的关系得到x1+x2=4﹣a,x1x2=①,
由于OA⊥OB可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,所以可得2x1x2+a(x1+x2)+a2=0②
由①②可得a=﹣1,满足△=56﹣16a﹣4a2>0.故a=﹣1.
[选做题]
22.已知p:|x﹣4|≤6,q:x2+3x≥0,若命题“p且q”和“¬p”都为假,求x的取值范围.
【考点】复合命题的真假.
【分析】先求出命题p、q为真时x的取值范围,由复合命题真值表知,若命题“p且q”和“¬p”都为假,则p为真q为假,由此求出x的取值范围.
【解答】解:命题p为真时:﹣2≤x≤10;
命题q为真时:x≤﹣3或x≥0.
由复合命题真值表知,
若命题“p且q”和“¬p”都为假,则p为真q为假.
∴⇒﹣2≤x<0.
故x的取值范围是{x|﹣2≤x<0}.
[选做题]
23.已知F1、F2为椭圆+=1(a>b>0)的左、右焦点,过F2做椭圆的弦AB.
(Ⅰ) 求证:△F1AB的周长是常数;
(Ⅱ) 若:△F1AB的周长为16,且|AF1|、|F1F2|、|AF2|成等差数列,求椭圆方程.
【考点】椭圆的简单性质.
【分析】(Ⅰ)由椭圆的定义知,|AF1|+|AF2|=|BF1|+|BF2|=2a,即可得出△F1AB的周长是常数.
(Ⅱ)由周长为16,得a=4; 又|AF1|、|F1F2|、|AF2|成等差数列,可得2|F1F2|=|AF1|+|AF2|,即4c=2a,解得c.再利用b2=a2﹣c2,即可得出.
【解答】解:(Ⅰ)由椭圆的定义知,|AF1|+|AF2|=|BF1|+|BF2|=2a,∴△F1AB的周长是常数4a.
(Ⅱ)由周长为16,得a=4; 又|AF1|、|F1F2|、|AF2|成等差数列,
∴2|F1F2|=|AF1|+|AF2|,
∴4c=2a,解得c=2.
b2=a2﹣c2=12.
∴椭圆的标准方程为: =1.
[选做题]
24.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a、b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(﹣∞,﹣1)上的最大值.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.
【分析】(1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;
(2)根据a2=4b,构建函数,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(﹣∞,﹣1)上的最大值.
【解答】解:(1)f(x)=ax2+1(a>0),则f'(x)=2ax,k1=2a,g(x)=x3+bx,则g′(x)=3x2+b,k2=3+b,
由(1,c)为公共切点,可得:2a=3+b ①
又f(1)=a+1,g(1)=1+b,
∴a+1=1+b,即a=b,代入①式可得:.
(2)由题设a2=4b,设
则,令h'(x)=0,解得:,;
∵a>0,∴,
x
(﹣∞,﹣)
﹣
)
h′(x)
+
﹣
+
h(x)
极大值
极小值
∴原函数在(﹣∞,﹣)单调递增,在单调递减,在)上单调递增
①若,即0<a≤2时,最大值为;
②若<﹣,即2<a<6时,最大值为
③若﹣1≥﹣时,即a≥6时,最大值为h(﹣)=1
综上所述:当a∈(0,2]时,最大值为;当a∈(2,+∞)时,最大值为.
2016年12月1日