- 572.75 KB
- 2021-06-17 发布
2019-2020第二学期期末高一年级数学考试问卷
一、选择题(共12小题,每题5分,共60分)
1.已知a、b、c满足a>b>c>0,则下列选项成立的是( )
A、ab>ac B、ab<ac C、 D、a2b<a2c
2.过点的直线平分了圆:的周长,则直线的倾斜角为( ).
A. B. C. D.
3.已知为等比数列,,,则( ).
A.7 B.5 C.-5 D.-7
4.已知,是两条不同直线,,是两个不同平面,则下列命题正确的是( )
A.若,垂直于同一平面,则与不平行
B.若,平行于同一平面,则与平行
C.若,不平行,则在内不存在与平行的直线
D.若,不平行,则与不可能垂直于同一平面
5.在中,,,,则等于( )。
A: B: C: D:
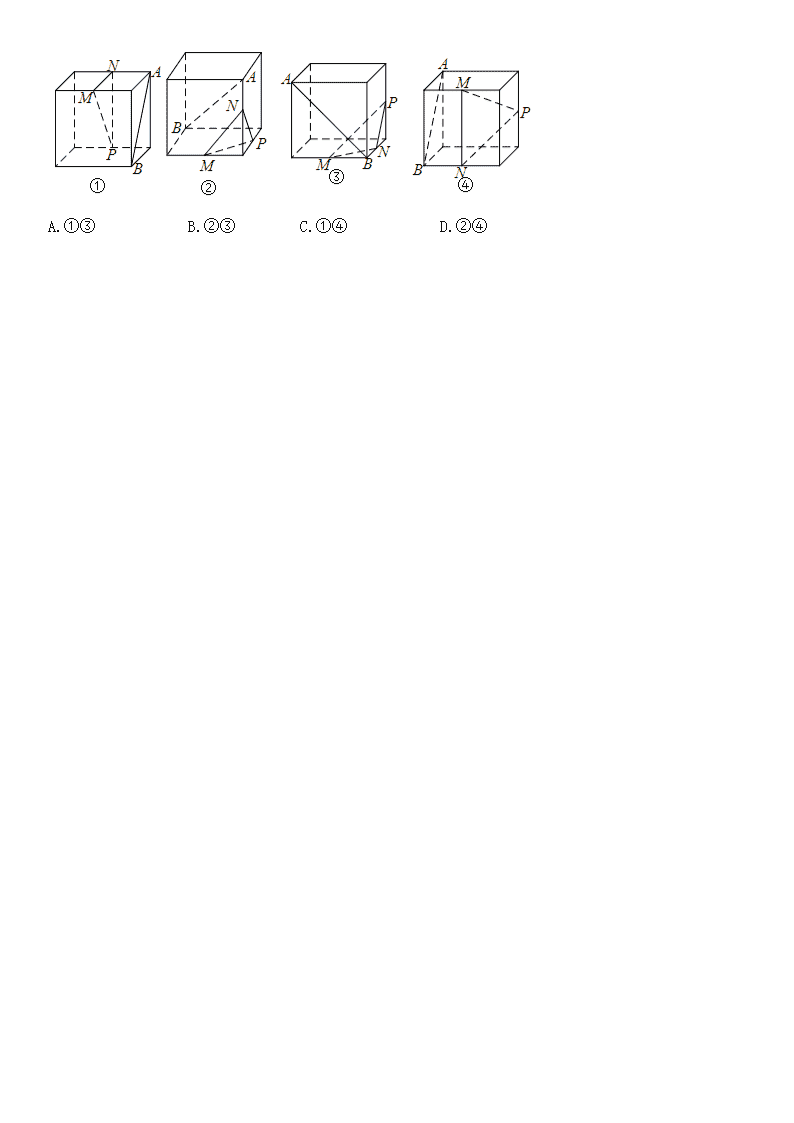
6.下列各图中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形的序号是( )。
A.①③ B.②③ C.①④ D.②④
7.设等差数列的公差为2,前n项和为,则下列结论正确的是()
A. B.
C. D.
8.如图⨀O所在平面,是⨀O的直径,是⨀O上一点,,,给出下列结论:①;②;③;④平面平面⑤是直角三角形
其中正确的命题的个数是( )
A.4 B.3 C.2 D.1
9.已知各顶点都在一个球面上的正四棱柱高为,体积为,则这个球的表面积是( )
A. B. C. D.
10.若动点,分别在直线和上移动,则线段AB的中点M到原点的距离的最小值为( )
A. B.2 C. D.
11.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一个各条棱都相等的四面体,四个氢原子分别位于该四面体的四个顶点上,碳原子位于该四面体的中心,它与每个氢原子的距离都是a,若将碳原子和氢原子均视为一个点,则任意两个氢原子之间的距离为( )
A. B. C. D.
12.△ABC的内角A,B,C所对的边长分别为a,b,c,已知角A=60°,角B为锐角,a=,△ABC周长的取值范围( )
A.(2,4] B.(4,6] C.[2−4,2+4] D.[−2,6]
二、填空题(共4小题,每小题5分,共20分)
13.已知实数x、y满足条件则的最大值为 .
14.已知长方体的顶点都在直径为3的球面上,,点E是的中点,则异面直线与所成角的大小为是 .
15.已知,,且,若恒成立,则实数的取值范围是_____。
16.设数列{an}中前n项的和Sn=2an+3n−7,则an=______.
17.已知直线L过两直线x-2y+4=0和x+y-2=0的交点,且点A(-1,0),B(3,4)到直线的距离相等,求直线L的方程。
18.已知:f(x)=x2+bx+c,不等式f(x)<0的解集是(0,4).
(1)求f(x)的解析式;
(2)若对于任意的x∈[−1,3],则不等式f(x)−t⩽2恒成立,求t的取值范围。
19.如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(1)设FC的中点为M,求证:OM∥面DAAF;
(2)求证:AF⊥面CBF.
20.已知:在△ABC中,内角A,B,C的对边分别为a,b,c,且=2c−ab
(1)求sinCsinA的值
(2)若cosB=,b=2,求△ABC的面积S.
21.已知数列的各项排成如图所示的三角形数阵,数阵中每一行的第一个数,,,,……构成等差数列,是的前n项和,且,.
(I)若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知,求的值;
(Ⅱ)设,求.
22.已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆C相切,求l1的方程;
(2)若l1与圆C相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,求证:|AM|·|AN|为定值.
2019-2020第二学期期末高一年级数学考试问卷
一、选择题(共12小题,每题5分,共60分)
1.已知a、b、c满足a>b>c>0,则下列选项成立的是( )
A、ab>ac B、ab<ac C、 D、a2b<a2c
【答案】A
解:因为a、b、c满足a>b>c>0,所以ab>ac,A正确.B:ab<ac⇒b<c,与题意不符,不正确;
C:⇒b>a,与题意不符,不正确;
D:a2b<a2c⇒b<c,与题意不符,不正确;
故选A.
2.过点的直线平分了圆:的周长,则直线的倾斜角为( ).
A. B. C. D.
【答案】D
本题考查圆的性质
圆是以圆心为对称中心的中心对称图形,也是以每条直径所在直线为对称轴的中心图形;
由知其圆心为;
直线平分了圆:的周长,则此直线过圆的圆心,于是其斜率为;所以其倾斜角为
3.已知为等比数列,,,则( ).
A.7 B.5 C.-5 D.-7
【答案】D
4.已知,是两条不同直线,,是两个不同平面,则下列命题正确的是( )
A.若,垂直于同一平面,则与不平行
B.若,平行于同一平面,则与平行
C.若,不平行,则在内不存在与平行的直线
D.若,不平行,则与不可能垂直于同一平面
【答案】D
项,因为垂直于同一平面的两条直线平行,故项正确。
项,若,垂直于同一平面,则与平行或相交,故项错误;
项,若,平行于同一平面,则与可能平行、相交或异面,故项错误;
项,若,不平行,则在内与两平面交线平行的直线与平行,故项错误;
故本题正确答案为。
5.在中,,,,则等于( )。
A: B: C: D:
【答案】D
因为,所以,又因为大边对大角,所以,所以角为锐角,所以。
故本题正确答案为D。
6.下列各图中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形的序号是( )。
A.①③ B.②③ C.①④ D.②④
【答案】A
①项,如图,作,连接,,得平面,因为,平面,所以平面,即平面,故①项正确;
②项,如图,连结,,,由已知可得平面平面;因为和平面相交,所以不平行于平面,故②项错误;
③项,如图,连接,,,由已知可得,因为,由平行的传递性可得,又因为,,,所以平面平面,又因为平面,所以平面,故③项正确;
④项,如图,因为,平面,若平面,又,则平面平面,由图可知平面不可能平行平面,所以不平行于平面,故④项错误。
综上,①③符合题意。
故本题正确答案为A。
7.设等差数列的公差为2,前n项和为,则下列结论正确的是()
A. B.
C. D.
【答案】C
将其代入
即可得答案为C
8.如图⨀O所在平面,是⨀O的直径,是⨀O上一点,,,给出下列结论:①;②;③;④平面平面⑤是直角三角形
其中正确的命题的个数是( )
A.4 B.3 C.2 D.1
【答案】A
因为,所以。因为,所以,因为,所以。因为,,所以。因为,,所以。故①⑤正确。
因为,,,所以,因为,所以,故②正确。
假设成立,因为,,所以。但已征得,与过平面外一点有且只有一条直线与已知平面垂直相矛盾,所以假设不成立。故③不正确。
因为,,所以平面平面。故④正确。
综上可得①②④⑤正确。
9.已知各顶点都在一个球面上的正四棱柱高为,体积为,则这个球的表面积是( )
A. B. C. D.
【答案】C
正四棱锥的底面面积为,所以此正四棱柱底面边长为2.
正四棱柱的体对角线长为.所以所求球的半径为,表面积为.
故C正确.
10.若动点,分别在直线和上移动,则线段AB的中点M到原点的距离的最小值为( )
A. B.2 C. D.
【答案】A
由题意知,M点的轨迹为平行于直线、且到、距离相等的直线l,故其方程为,
到原点的距离的最小值为.
所以A选项是正确的;
11.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一个各条棱都相等的四面体,四个氢原子分别位于该四面体的四个顶点上,碳原子位于该四面体的中心,它与每个氢原子的距离都是a,若将碳原子和氢原子均视为一个点,则任意两个氢原子之间的距离为( )
A. B. C. D.
【答案】B
显然,四面体的四个顶点在以中心(碳原子)为球心,中心到各顶点(氢原子)的距离为半径的球面上,
如图,将此正四面体ABCD补成正方体,
其中A'、B'、D'也在球面上,
设任意两个氢原子之间的距离为x,则.
、、之间的关系是,,
因此,
,即碳原子到各个氢原子的距离.
所以B选项是正确的
12.△ABC的内角A,B,C所对的边长分别为a,b,c,已知角A=60°,角B为锐角,a=,△ABC周长的取值范围( )
A.(2,4] B.(4,6] C.[2−4,2+4] D.[−2,6]
【答案】
由题意,在△ABC中,,
可得b=4sinB,c=4sinC,
故选:B.
二、填空题(共4小题,每小题5分,共20分)
13.已知实数x、y满足条件则的最大值为 .
【答案】-1
易知可行域为一个三角形,
验证知在点时,取得最大值-1,
故填-1.
14.已知长方体的顶点都在直径为3的球面上,,点E是的中点,则异面直线与所成角的大小为是 .
【答案】
先画出大致图形
先将平移到FD,则是异面直线与所成角,
由题可知,,得,而,则,
计算得,,,
由余弦定理可得,即
故答案为
15.已知,,且,若恒成立,则实数的取值范围是_____。
【答案】
因为,要使恒成立,所以,解得。
故本题正确答案为。
16.设数列{an}中前n项的和Sn=2an+3n−7,则an=______.
【答案】2n−1+3
由Sn=2an+3n−7①,
取n=1得:a1=2a1+3−7,即a1=4.
当n⩾2时,Sn−1=2an−1+3(n−1)−7②,
①−②得:an=2an−2an−1+3,
即an−2an−1=−3.
an−3=2(an−1−3)(n⩾2).
∵a1−3=1≠0,
∴数列{an−3}是以1为首项,以2为公比的等比数列,
∴an−3=2n−1.
an=2n−1+3.
故答案为:2n−1+3.
17.已知直线L过两直线x-2y+4=0和x+y-2=0的交点,且点A(-1,0),B(3,4)到直线的距离相等,求直线L的方程。
【答案】y=2或y=x+2
18.已知:f(x)=x2+bx+c,不等式f(x)<0的解集是(0,4).
(1)求f(x)的解析式;
(2)若对于任意的x∈[−1,3],则不等式f(x)−t⩽2恒成立,求t的取值范围。
【答案】
(1)f(x)=x2+bx+c,不等式f(x)<0的解集是(0,4),
可得0和4是方程x2+bx+c=0的两根,
即有0+4=−b,0×4=c,解得b=−4,c=0,
f(x)=x2−4x;
(2)对于任意的x∈[−1,3],则不等式f(x)−t⩽2恒成立,
即为2+t⩾f(x)在[−1,3]的最大值,
由f(x)的对称轴x=2,且f(−1)=1+4=5,f(3)=9−12=−3,
可得f(x)的最大值为5,
即有2+t⩾5,解得t⩾3,
则t的取值范围为[3,+∞).
19.如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(1)设FC的中点为M,求证:OM∥面DAAF;
(2)求证:AF⊥面CBF.
【答案】(1)设DF的中点为N,连接MN,
则MN∥12CD,MN=12CD,
又∵AO∥12CD,AO=12CD,
∴MN∥AO,MN=AO,
∴MNAO为平行四边形,
∴OM∥AN.
又∵AN⊂面DAF,OM⊄面DAF,
∴OM∥面DAF.
(2)∵面ABCD⊥面ABEF,CB⊥AB,CB⊂面ABCD,面ABCD∩面ABEF=AB,
∴CB⊥面ABEF.
∵AF⊂面ABEF,
∴AF⊥CB.
又∵AB为圆O的直径,
∴AF⊥BF,
又∵CB∩BF=B,CB,BF⊂面CBF.
∴AF⊥面CBF.
20.已知:在△ABC中,内角A,B,C的对边分别为a,b,c,且=2c−ab
(1)求sinCsinA的值
(2)若cosB=,b=2,求△ABC的面积S.
【答案】
(1)∵==,
∴cosAsinB−2sinBcosC=2cosBsinC−sinAcosB,
∴sinAcosB+cosAsinB=2sinBcosC+2cosBsinC,
∴sin(A+B)=2sin(B+C),
∴sinC=2sinA,
∴=2;
(2)由(1)可得c=2a,
由余弦定理可得b2=a2+c2−2accosB,
∴4=a2+4a2−a2,
解得a=1,则c=2,
∵cosB=,
∴sinB=,
∴S=acsinB=×1×2×=.
21.已知数列的各项排成如图所示的三角形数阵,数阵中每一行的第一个数,,,,……构成等差数列,是的前n项和,且,.
(I)若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知,求的值;
(Ⅱ)设,求.
【答案】(I)为等差数列,设公差为d,,,
,,
分
设从第三行起每行的公比都是q,且,,故分
,
故是数阵中第10行第5个数,
而分
(2)由①得bn=n,所以Sn=,那么
那么
22.已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆C相切,求l1的方程;
(2)若l1与圆C相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,求证:|AM|·|AN|为定值.
【答案】(1)如图:
①若直线l的斜率不存在,即直线为x=1,由题知圆心为(3,4),半径r=2,故符合题意;
②若直线l的斜率存在,设切线方程为y=k(x-1),即kx-y-k=0,由题意知,圆心(3,4)到直线l的距离等于半径2,即
解得k=,
故所求的切线方程为x=1或3x-4y-3=0.