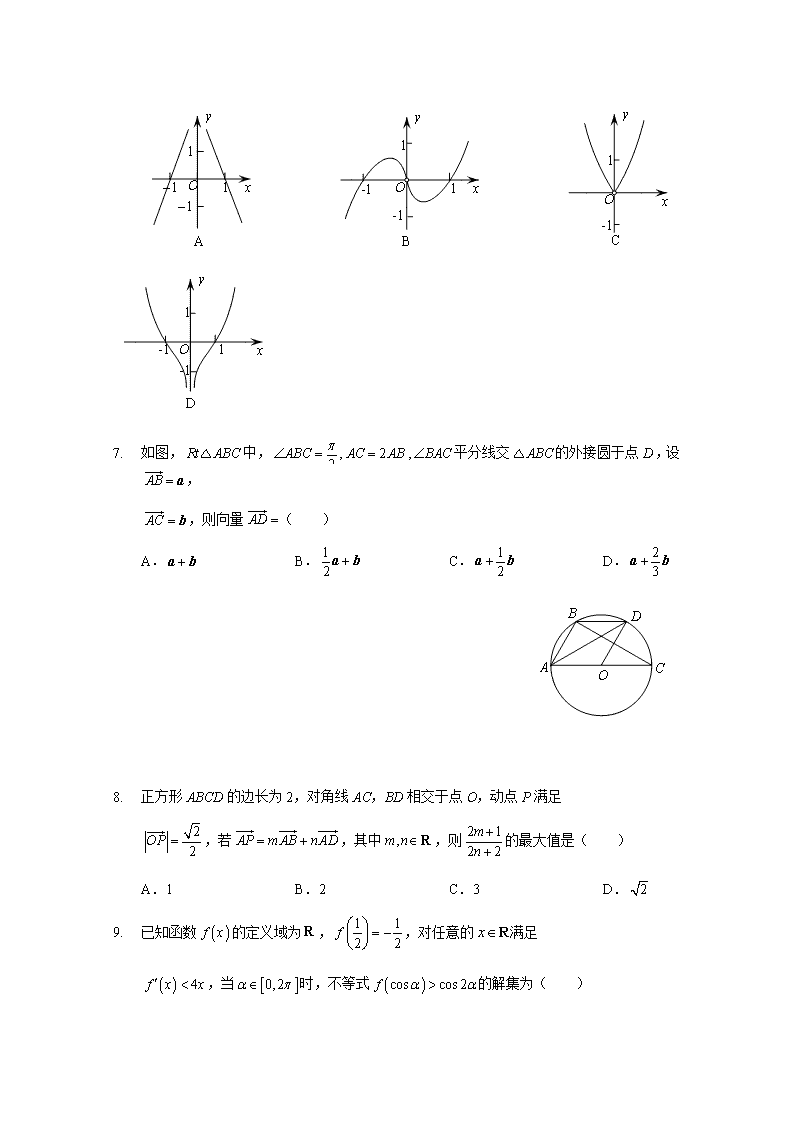- 327.45 KB
- 2021-02-26 发布
2019学年杭二高三上期中
一、选择题:每小题4分,共40分
1. 若复数满足,则的虚部为( )
A. B. C.2 D.
2. 若,,且,则向量,的夹角为( )
A. B. C. D.
3. 若,则( )
A.1 B. C. D.
4. 已知各项不为0的等差数列满足,数列是等比数列且,则等于( )
A. B. C. D.
5. 若变量,满足,则的最大值是( )
A.4 B.9 C.16 D.18
6. 函数的图象大致为( )
1. 如图,中,,,平分线交的外接圆于点,设,
,则向量( )
A. B. C. D.
2. 正方形ABCD的边长为2,对角线AC,BD相交于点O,动点P满足
,若,其中,则的最大值是( )
A.1 B.2 C.3 D.
3. 已知函数的定义域为,,对任意的满足
,当时,不等式的解集为( )
A. B. C. D.
1. 已知函数的图象在点处的切线为l:,若函数满足(其中I为函数的定义域),当时,恒成立,则
称为函数“转折点”,已知函数在区间上存在一个“转折点”,则a的取值范围是( )
A. B. C. D.
二、填空题:单空题每题4分,多空题每题6分
2. 已知集合,,若,则实数a的取值范围是 ,
若,则实数a的取值范围是 .
3. 若,则 .
4. 设函数,则不等式的解集为 ,若存在实数x满足成立,则实数a的取值范围是 .
5. 对于函数,若存在区间,当时的值域为,则称为k倍值函数.若是k倍值函数,则实数k的取值范围是 .
6. 函数的图象与其对称轴在y轴右侧的交点从左到右依次记为,,,,,在点列中存在三个不同的点,,,使得是等腰直角三角形,将满足上述条件的值从小到大组成的数列记为,则 .
7. 点D在的边AC上,且,,,则的最大值为 .
8. 已知向量,向量满足,若对任意的,记的最小值为M,则M的最大值为 .
三、解答题:5小题,共74分
18. 设函数.
(1)求函数的递增区间;
(2)在中,,,分别为内角,,的对边,若,,
且,求的面积.
19. 如图,四棱锥中,底面,,
,过点作平面垂直于直线,分别交,于点,.
(1)求的长度;
(2)求平面与平面所成的锐二面角的余弦值.
20. 已知等比数列的前项和为,,,成等差数列,且.
(1)求数列的通项公式;
(2)若,求数列的前项和.
18. 设椭圆的焦距为2,且点在椭圆上,左右顶点为,,左右焦点为,.过点作斜率为的直线交椭圆于轴上方的点,交直线于点,直线与椭圆的另一个交点为,直线与直线交于点.
(1)求椭圆的标准方程;
(2)若,求的值;
(3)若,求实数的取值范围.
19. 已知,,其中实数.
(1)求的最大值;
(2)若对于任意实数恒成立,求实数的取值范围.