高考理科数学专题复习练习7.2二元一次不等式(组)与简单的线性规划问题 3页

第七章不等式　推理与证明 ‎7.2二元一次不等式(组)与简单的线性规划问题 专题1‎ 二元一次不等式(组)表示的平面区域问题 ‎■(2015河南省洛阳市高考数学一模,二元一次不等式(组)表示的平面区域问题,选择题,理11)若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组x+y-7<0,‎x-3y+1<0,‎‎3x-y-5>0‎表示的平面区域有公共点,则实数λ的取值范围是(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A.‎-∞,-‎‎13‎‎7‎∪(9,+∞) B.‎-‎13‎‎7‎,1‎∪(9,+∞)‎ C.(1,9) D.‎‎-∞,-‎‎13‎‎7‎ 解析:(3λ+1)x+(1-λ)y+6-6λ=0等价为λ(3x-y-6)+(x+y+6)=0,‎ 则‎3x-y-6=0,‎x+y+6=0.‎解得x=0,‎y=-6,‎ 即直线过定点D(0,-6).‎ 作出不等式组对应的平面区域如图:其中A(2,1),B(5,2),此时AD的斜率k=‎-6-1‎‎0-2‎‎=‎‎7‎‎2‎,BD的斜率k=‎-6-2‎‎0-5‎‎=‎‎8‎‎5‎,‎ 当直线过A时,λ=9,当直线过B时,λ=-‎13‎‎7‎,‎ 则若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组x+y-7<0,‎x-3y+1<0,‎‎3x-y-5>0‎ 表示的平面区域有公共点,则满足直线的斜率‎8‎‎5‎‎<‎3λ+1‎λ-1‎<‎‎7‎‎2‎,解得λ∈‎-∞,-‎‎13‎‎7‎∪(9,+∞),故选A.‎ 答案:A 专题2‎ 与目标函数有关的最值问题 ‎■(2015甘肃省白银市会宁二中高考数学模拟,与目标函数有关的最值问题,选择题,理9)已知变量x,y满足x-y-2≤0,‎x+2y-5≥0,‎y-2≤0,‎则u=‎3x+yx+1‎的取值范围是(　　)‎ A.‎5‎‎2‎‎,‎‎14‎‎5‎ B.‎‎-‎1‎‎2‎,-‎‎1‎‎5‎ C.‎-‎1‎‎2‎,‎‎5‎‎2‎ D.‎‎-‎5‎‎2‎,‎‎14‎‎5‎ 解析:∵u=‎3x+yx+1‎=3+y-3‎x+1‎,设k=y-3‎x+1‎.‎ ‎∴u=3+k,而k=y-3‎x+1‎表示直线PQ连线的斜率,‎ 其中P(x,y),Q(-1,3).‎ 作出不等式组x-y-2≤0,‎x+2y-5≥0‎y-2≤0‎表示的平面区域,‎ 得到如图所示的△ABC及其内部的区域,其中A(1,2),B(4,2),C(3,1).‎ 设P(x,y)为区域内的动点,‎ 可得当P与A点重合时,kPQ=-‎1‎‎2‎达到最小值;当P与B点重合时,kPQ=-‎1‎‎5‎达到最大值.∴u=3+k的最大值为-‎1‎‎5‎+3=‎14‎‎5‎;最小值为-‎1‎‎2‎+3=‎5‎‎2‎.‎ 因此,u=‎3x+yx+1‎的取值范围是‎5‎‎2‎‎,‎‎14‎‎5‎.故选A.‎ 答案:A ‎■(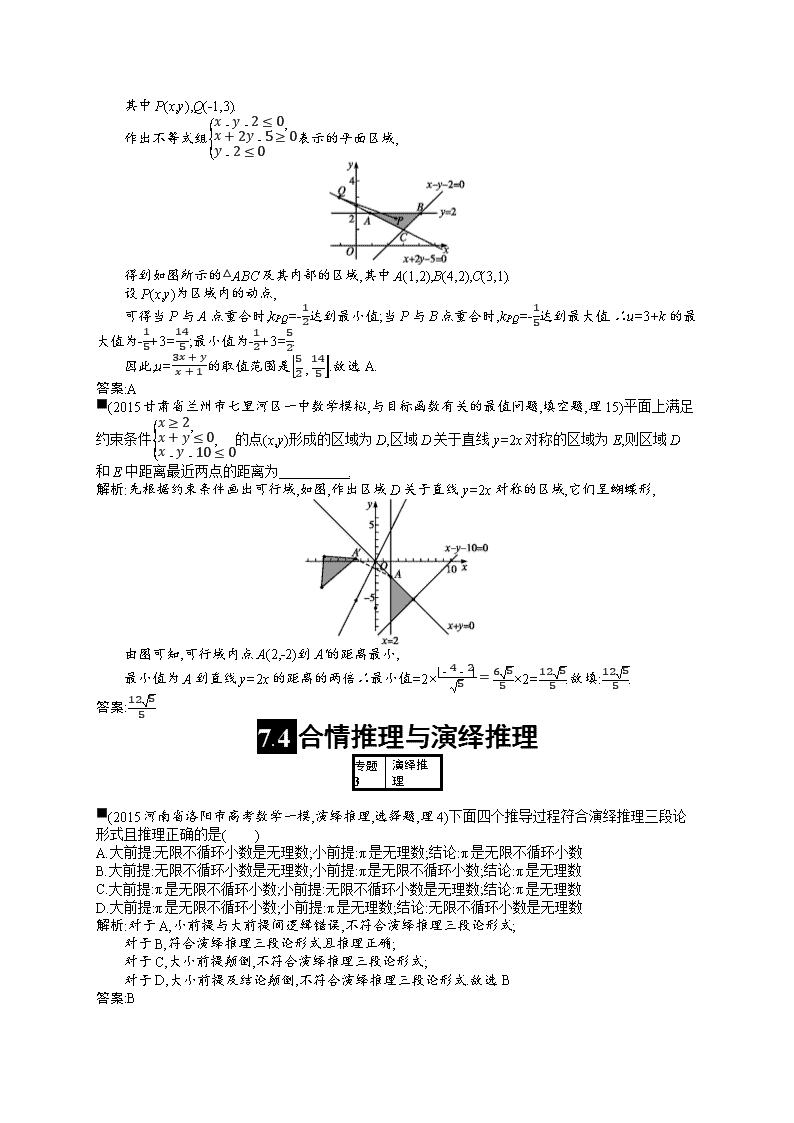2015甘肃省兰州市七里河区一中数学模拟,与目标函数有关的最值问题,填空题,理15)平面上满足约束条件x≥2,‎x+y≤0,‎x-y-10≤0‎的点(x,y)形成的区域为D,区域D关于直线y=2x对称的区域为E,则区域D和E中距离最近两点的距离为　　　　　. ‎ 解析:先根据约束条件画出可行域,如图,作出区域D关于直线y=2x对称的区域,它们呈蝴蝶形,‎ 由图可知,可行域内点A(2,-2)到A'的距离最小,‎ 最小值为A到直线y=2x的距离的两倍∴最小值=2×‎|-4-2|‎‎5‎‎=‎‎6‎‎5‎‎5‎×2=‎12‎‎5‎‎5‎.故填:‎12‎‎5‎‎5‎.‎ 答案:‎‎12‎‎5‎‎5‎ ‎7.4合情推理与演绎推理 专题3‎ 演绎推理 ‎■(2015河南省洛阳市高考数学一模,演绎推理,选择题,理4)下面四个推导过程符合演绎推理三段论形式且推理正确的是(　　)‎ A.大前提:无限不循环小数是无理数;小前提:π是无理数;结论:π是无限不循环小数 B.大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 C.大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 D.大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 解析:对于A,小前提与大前提间逻辑错误,不符合演绎推理三段论形式;‎ 对于B,符合演绎推理三段论形式且推理正确;‎ 对于C,大小前提颠倒,不符合演绎推理三段论形式;‎ 对于D,大小前提及结论颠倒,不符合演绎推理三段论形式.故选B 答案:B