- 1.31 MB
- 2021-06-08 发布
成都龙泉中学高2014级高三上期12月月考试题
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
注意事项:
1.必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.
2.考试结束后,将本试题卷和答题卡一并交回。
1. 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则等于( )
A. B. C. D.
2.( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知点...,则向量在方向上的投影( )
A. B. C. D.
4.已知等比数列的前10项的积为32,则下列命题为真命题的是( )
A.数列的各项均为正数 B.数列中必有小于的项
C.数列的公比必是正数 D.数列的首项和公比中必有一个大于1.
5.设实数x,y满足约束条件,则z=的取值范围是( )
A. B. C. D.
6.设函数的图象为,下面结论中正确的是( )
A.函数的最小正周期是
B.函数在区间上是增函数
C.图象可由函数的图象向右平移个单位得到
D.图象关于点对称
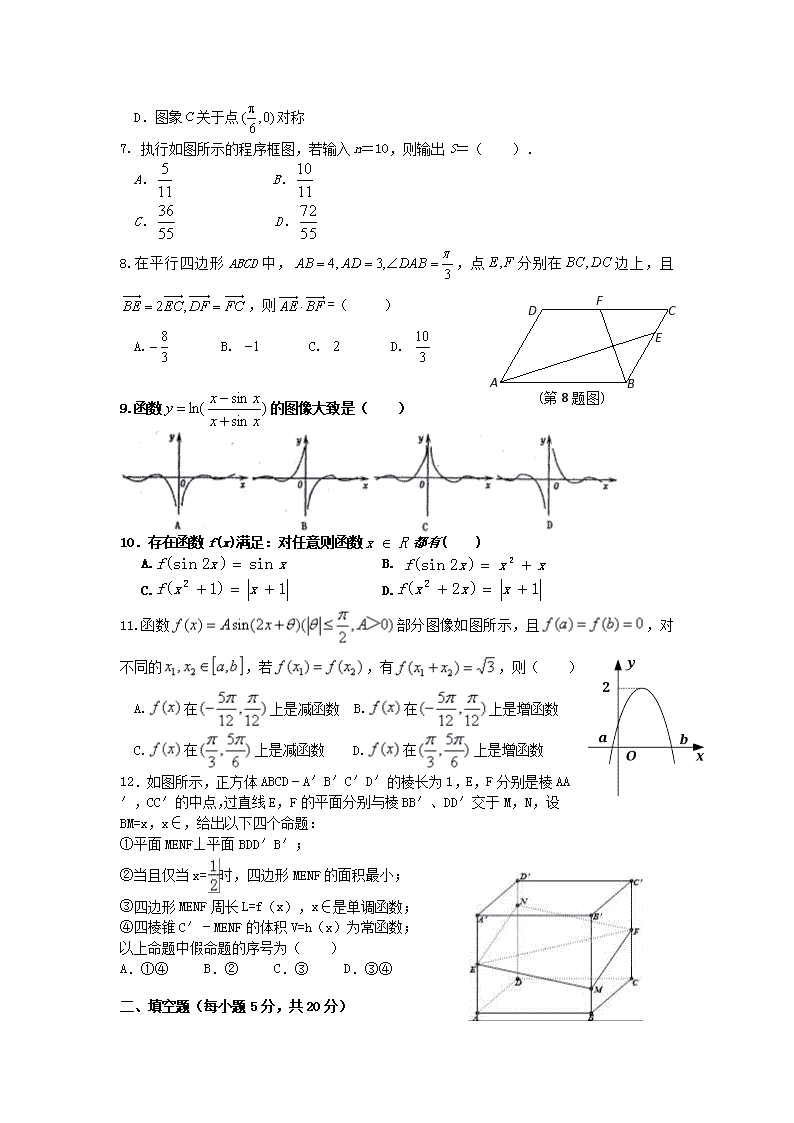
7. 执行如图所示的程序框图,若输入n=10,则输出S=( ).
A. B.
C. D.
F
E
B
C
D
A
(第8题图)
8.在平行四边形ABCD中,,点分别在边上,且,则=( )
A. B. C. D.
9.函数的图像大致是( )
10.存在函数f(x)满足:对任意则函数都有( )
A. B.
C. D.
11.函数部分图像如图所示,且,对不同的,若,有,则( )
A.在上是减函数 B.在上是增函数
C.在上是减函数 D.在上是增函数
12.如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈,给出以下四个命题:
①平面MENF⊥平面BDD′B′;
②当且仅当x=时,四边形MENF的面积最小;
③四边形MENF周长L=f(x),x∈是单调函数;
④四棱锥C′﹣MENF的体积V=h(x)为常函数;
以上命题中假命题的序号为( )
A.①④ B.② C.③ D.③④
二、填空题(每小题5分,共20分)
13.在平面直角坐标系中,角终边过点,则的值为. ________________.
14、某校为了了解本校高三学生学习心理状态,采用系统抽样方法从800人中抽取40人参加某种测试,为此将学生随机编号为1,2,…,800,分组后在第一组采用简单随机抽样的方法抽到号码为18,抽到的40人中,编号落入区间的人做试卷A,编号落入区间的人做试卷B,其余的人做试卷C,则做试卷C的人数为 .
15.一个几何体的三视图如图所示,则该几何体的体积为 .
16.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数被称为狄利克雷函数,则关于函数有如下四个命题:
①; ②函数是偶函数;
③任取一个不为零的有理数,对任意的恒成立;
④存在三个点,使得为等边三角形.
其中正确命题的序号有________
三、解答题(共6小题,共70分.解答应写出文字说明,演算步骤或证明过程)
17. (本小题满分12分)
已知各项为正数的数列的前项和为且满足
(Ⅰ)数列的通项;
(Ⅱ)令,求数列的前项和.
18.(本小题满分12分)
已知函数的最小正周期为.
(1)求的值; (2)讨论在区间上的单调性.
19、(本小题满分12分)
已知正四棱柱ABCD—A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点F为BD1中点.
(1)证明EF为BD1与CC1的公垂线;
(2)求点D1到面BDE的距离.
20. (本小题满分12分)某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号
A1
A2
A3
A4
A5
质量指标(x, y, z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标(x, y, z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
21.(本小题12分)已知椭圆的右焦点为,且点在椭圆上.
(1)求该椭圆的方程;
(2)过椭圆上异于其顶点的任意一点作圆的两条切线,切点分别为(不在坐标轴上),若直线在轴,轴上的截距分别为,证明为定值;
(3)若是椭圆上不同的两点,轴,圆过且椭圆上任意一点都不在圆内,则称圆为该椭圆的一个内切圆,试问:椭圆
是否存在过左焦点的内切圆?若存在,求出圆心的坐标;若不存在,说明理由.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.
22. (本小题满分10分)选修4—4;坐标系与参数方程
已知曲线的极坐标方程是.以极点为平面直角坐标系的原点,极轴为轴的正半轴,建立平面直角坐标系,直线的参数方程是(为参数).
(1)将曲线的极坐标方程化为直角坐标方程;
(2)若直线与曲线相交于、两点,且,求直线的倾斜角的值.
23.(本小题满分12分)选修4-5:不等式选讲
已知函数,.
(Ⅰ)解不等式;
(Ⅱ)若对任意的,都有,使得成立,求实数的取值范围.
成都龙泉中学2014级高三上期12月月考试题
数学(文史类)参考答案
1—5 CADCD 6—10 DACAD 11—12 BC
13. 14.12 16.②③④
17.解:(Ⅰ)(ⅰ)当时,,所以:
所以:或者(舍去)
①
(ⅱ)当时, ②
所以:①-②得:()
分解因式得:;又
所以:()
故数列是以首相为2,公差为2的等差数列
所以:;
(Ⅱ)
.
18.(本小题满分12分)
(4) 因为函数的最小正周期为,
故,所以,. ……6分
(2).故,
当时,即时,为减函数;
当时,即时,为增函数.
所以,的减区间为,增区间为.…12分
19解:(1)证法一:取BD中点M.连结MC,FM .
∵F为BD1中点 , ∴FM∥D1D且FM=D1D .(2分)
又EC=CC1且EC⊥MC ,∴四边形EFMC是矩形
∴EF⊥CC1.(4分) 又CM⊥面DBD1 .∴EF⊥面DBD1 .
∵BD1面DBD1 . ∴EF⊥BD1 . 故EF为BD1 与CC1的公垂线.
(Ⅱ)解:连结ED1,有VE-DBD1=VD1-DBE .
由(Ⅰ)知EF⊥面DBD1 ,设点D1到面BDE的距离为d.
故点D1到平面DBE的距离为.
法2:建立空间直角坐标系D-xyz如图所示。易得面DBE的一个法向量。
所以D1到平面DBE的距离. (12分)
20.解:
21. 解(1)由已知,,
由椭圆定义
所以椭圆方程为 …………………….2
(2)设,
则,,
在直线上,
点均在直线上,
即,由此得, ……….4
满足,即
…………………….6
(3)不妨设,圆心,
所以圆,
由内切圆定义知,椭圆上的点到圆心的距离的最小值为,
设是椭圆上任意一点,
,
当时,最小,所以,①
假设椭圆上存在过的内切圆,则,②
又在椭圆上,即,③
由①②③得:或,…………………….10
当时,不合题意,舍去经验证满足条件,
综上,存在这样的内切圆,圆心为 …………………….12
22.(本小题满分10分)选修4—4;坐标系与参数方程
【答案】(1);(2)或.
解:(1)由得.
∵,,,
∴曲线的直角坐标方程为,即. ...5分
(2)将代入圆的方程得,
化简得.
设两点对应的参数分别为、,则
∴.
∴,,或. ...10分
23.本题满分10分
解析:(1)由得,,解得.
所以原不等式的解集为 5分
(2)因为对任意,都有,使得=成立
所以,
有,
所以从而或 10分