2020高中数学 每日一题之快乐暑假 第17天 测量距离问题 理 新人教A版 4页

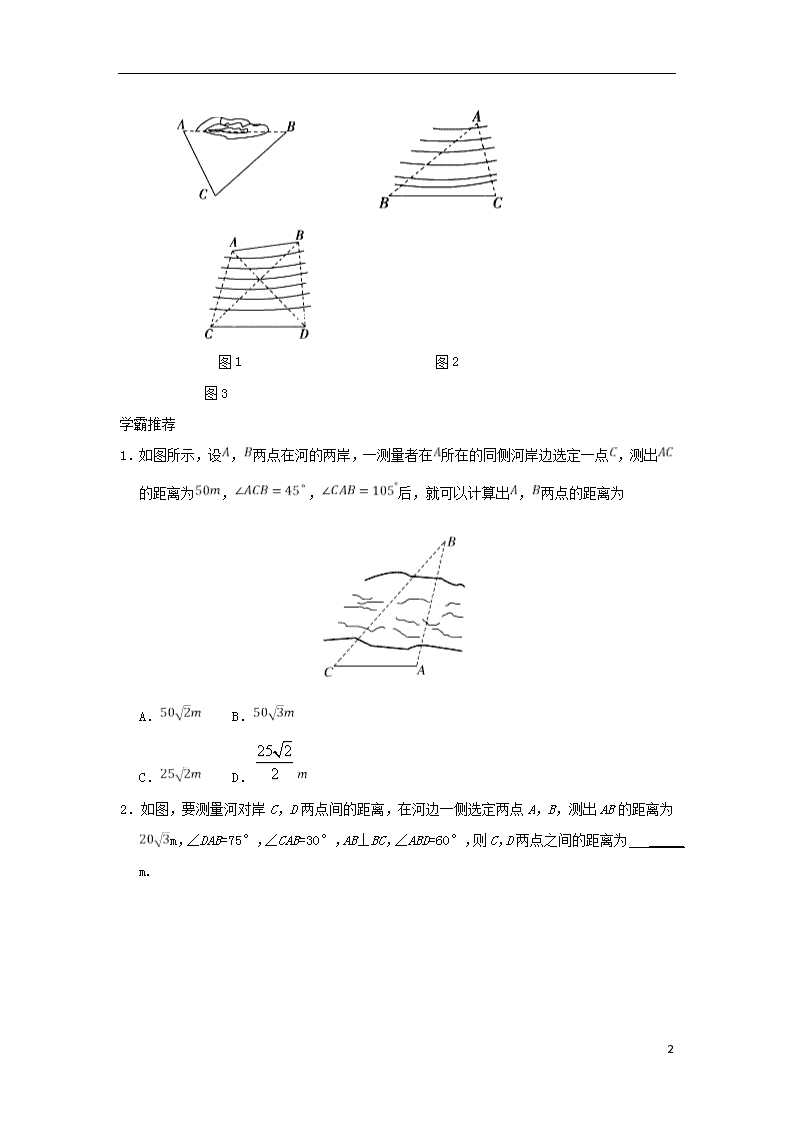
第17天 测量距离问题 高考频度：★★☆☆☆ 难易程度：★★☆☆☆‎ 典例在线 如图，在高速公路建设中需要确定隧道的长度，工程技术人员已测得隧道两端的两点A，B到点C的距离AC＝BC＝‎1 km，且C＝120°，则A，B两点间的距离为 ‎ ‎ A． B．‎ C． D．‎ ‎【参考答案】A ‎ ‎ ‎【解题必备】当的长度不可直接测量时，求，之间的距离有以下三种类型．‎ ‎（1）如图1，A，B之间不可达也不可视，计算方法：测量，及角，由余弦定理可得．‎ ‎（2）如图2，B，C与点A可视但不可达，计算方法：测量，角，角，则，由正弦定理可得．‎ ‎（3）如图3，C，D与点A，B均可视不可达，计算方法：测量 在中由正弦定理求，在中由正弦定理求，在中由余弦定理求．‎ 4‎ ‎ ‎ 图1 图2 图3‎ 学霸推荐 ‎1．如图所示，设，两点在河的两岸，一测量者在所在的同侧河岸边选定一点，测出的距离为，，后，就可以计算出，两点的距离为 ‎ ‎ A． B．‎ C． D．‎ ‎2．如图，要测量河对岸C，D两点间的距离，在河边一侧选定两点A，B，测出AB的距离为m，∠DAB=75°，∠CAB=30°，AB⊥BC，∠ABD=60°，则C，D两点之间的距离为 _____ m.‎ 4‎ ‎ ‎ ‎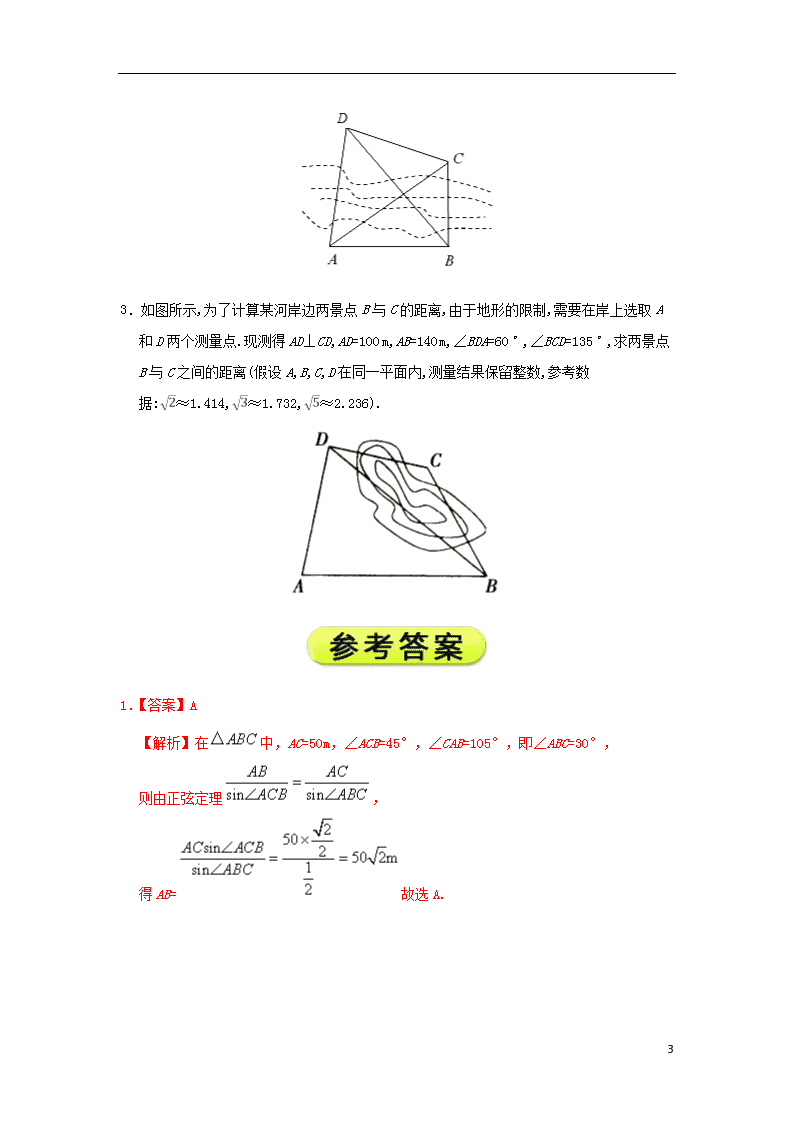3．如图所示,为了计算某河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点.现测得AD⊥CD,AD=‎100 m,AB=‎140 m,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A,B,C,D在同一平面内,测量结果保留整数,参考数据:≈1.414,≈1.732,≈2.236).‎ ‎ ‎ ‎ ‎ ‎1．【答案】A ‎【解析】在中，AC=‎50m，∠ACB=45°，∠CAB=105°，即∠ABC=30°，‎ 则由正弦定理，‎ 得AB=故选A.‎ 4‎ ‎ ‎ ‎3．【解析】在中,设BD为x,则BA2=BD2+AD2-2BD·AD·cos ∠BDA,‎ 即1402=x2+1002-2×100×x×cos 60°,整理,得x2-100x-9600=0,‎ 解得x1=160,x2=-60(舍去),故BD=160(m).‎ 在中,由正弦定理,得,‎ 又AD⊥CD,∠BDA=60°,所以∠CDB=30°,‎ 所以BC·sin 30°=80≈113(m).‎ 即两景点B与C之间的距离约为‎113 m.‎ 4‎