天津市南开区南大奥宇培训学校2020届高三4月月考数学试题（无答案） 4页

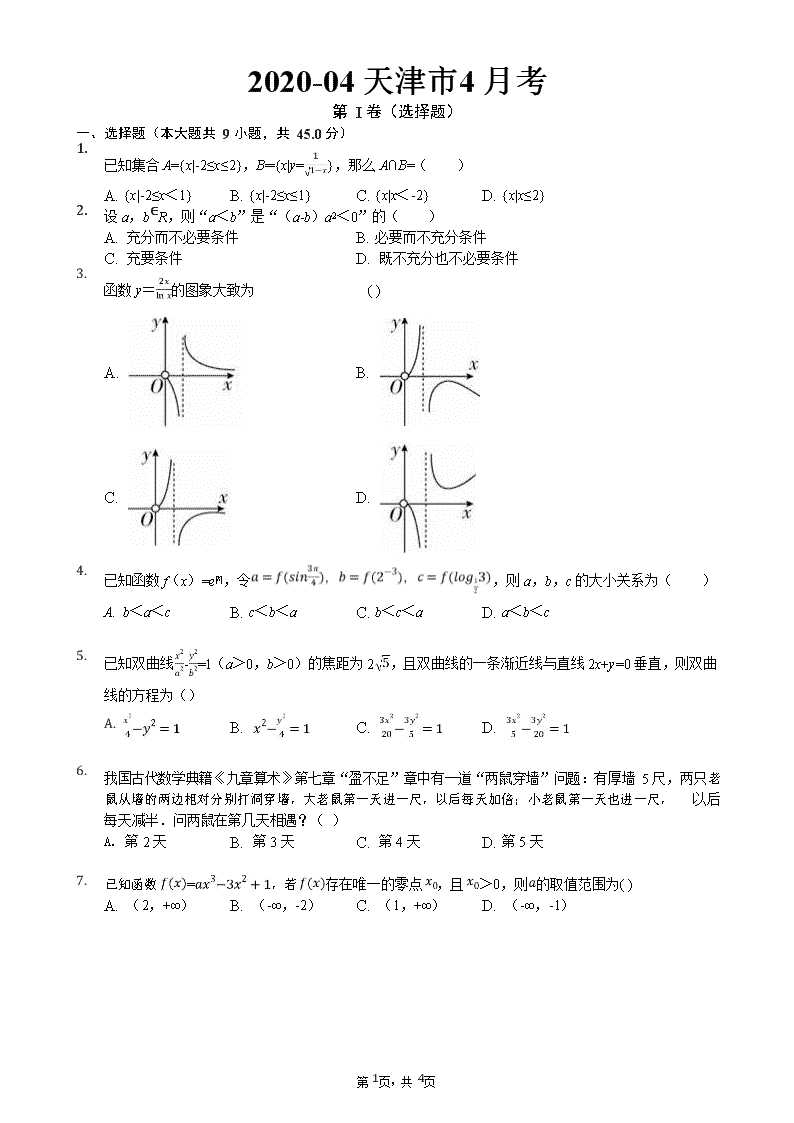
‎2020-04 天津市4 月考 第 I 卷（选择题）‎ 一、选择题（本大题共 9 小题，共 45.0 分）‎ ‎1. 已知集合 A={x|-2≤x≤2}，B═{x|y=}，那么 A∩B=（ ）‎ A. {x|-2≤x＜1} B. {x|-2≤x≤1} C. {x|x＜-2} D. {x|x≤2}‎ ‎2. 设 a，b∈R，则“a＜b”是“（a-b）a2＜0”的（ ）‎ A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 3. 函数 y＝的图象大致为 ( )‎ A. B.‎ C. D.‎ 4. 已知函数 f（x）=e|x|，令，则 a，b，c 的大小关系为（ ）‎ A. b＜a＜c B. c＜b＜a C. b＜c＜a D. a＜b＜c ‎-‎ 5. 已知双曲线 =1（a＞0，b＞0）的焦距为 2 ，且双曲线的一条渐近线与直线 2x+y=0 垂直，则双曲 线的方程为（）‎ A. B. C. D.‎ 6. 我国古代数学典籍《九章算术》第七章“盈不足”章中有一道“两鼠穿墙”问题：有厚墙 5 尺，两只老鼠从墙的两边相对分别打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺， 以后每天减半．问两鼠在第几天相遇？（ ）‎ A. 第 2 天 B. 第 3 天 C. 第 4 天 D. 第 5 天 7. 已知函数 = ，若 存在唯一的零点 ，且 ＞0，则 的取值范围为( )‎ A. （2，+∞） B. （-∞，-2） C. （1，+∞） D. （-∞，-1）‎ 第 4页，共 4页 3. 已知正三角形 ABC 的边长为 1，点 P 是 AB 边上的动点，点 Q 是 AC 边上的动点，且 ‎，则 的最大值为（ ）‎ A. B. C. D. ‎ 4. 若函数在 上是增函数，则ω的取值范围是（ ）‎ A. （0，1] B. （0，] C. [1，+∞） D. ‎ 第 II 卷（非选择题）‎ 二、填空题（本大题共 6 小题，共 30.0 分）‎ 5. 已知复数 z= ，则 z 的实部为 ．‎ ‎-‎ 6. 二项式（ ）5 的展开式中常数项为 （用数字作答）．‎ 7. 将参加夏令营的 600 名学生编号为 001,002,…，600.采用系统抽样的方法抽取一个容量为 50 的样本， 且随机抽得的号码为 003，这 600 名学生分住在三个营区，从 001 到 300 在第一营区，从 301 到 495 在第二营区，从 496 到 600 在第三营区，三个营区被抽中的人数依次为 .‎ 8. 已知两圆 x2+y2=1 和 x2+y2-6x-8y+m=0，当 m= 时，两圆外切：当 m= 时，两圆内切．‎ 9. 在△ABC 中，已知 A=， ，若 BC=，D 为 AB 的中点，则 cosC= ，CD 的长为 ．‎ 10. 已知函数 f（x）=ln（e2x+1）﹣mx 为偶函数，其中 e 为自然对数的底数，则 m= ，若 a2+ab+4b2≤m， 则 ab 的取值范围是 ．‎ 三、解答题（本大题共 5 小题，共 75.0 分）‎ 11. ‎（本题满分 14 分）为响应党中央号召，学校以“科学防疫”为主题举行在线知识竞赛．现有 10 道题， 其中 6 道甲类题，4 道乙类题，王同学从中任取 3 道题解答．‎ ‎（Ⅰ）求王同学至少取到 2 道乙类题的概率（5 分）；‎ ‎（Ⅱ）如果王同学答对每道甲类题的概率都是 ，答对每道乙类题的概率都是 ，且各题答对与否相互独立，已知王同学恰好选中 2 道甲类题，1 道乙类题，用 X 表示王同学答对题的个数，求随机变量 X 的分布列和数学期望（9 分）．‎ 第 4页，共 4页 3. ‎（本题满分 15 分）如图，四棱锥 P-ABCD 中，底面 ABCD 是矩形，面PAD⊥面 ABCD，且△PAD 是边长为 2 的等边三角形，PC=，M 在PC 上，且 PA∥面 MBD （1） 求证：M 是 PC 的中点；（4 分）‎ （2） 求直线 PA 与 MB 所成角的正切值；（5 分）‎ （3） 在 PA 上是否存在点 F，使二面角 F-BD-M 为直角？若存在，求出 的值；若不存在，说明理由．（6 分）‎ 4. ‎（本题满分 15 分）已知数列{an}是等比数列，数列{bn}是等差数列，且 a1=3，b2=a2，b5=a3+3，b8=a4．‎ ‎（Ⅰ）求数列{an}的通项公式 an；（5 分）‎ ‎（Ⅱ）令 cn=log2，证明： ＜1（n∈N*，n≥2）；（5 分）‎ ‎（Ⅲ）求 （n∈N*）．（5 分）‎ 第 4页，共 4页 3. ‎（本题满分 15 分）已知椭圆 C：+ =1（a＞b＞0）的焦距为 2，左右焦点分别为 F1，F2，以原点 O 为圆心，以椭圆 C 的半短轴长为半径的圆与直线 3x-4y+5=0 相切．‎ ‎（Ⅰ）求椭圆 C 的方程；（4 分）‎ ‎（Ⅱ）设不过原点的直线 l：y=kx+m 与椭圆 C 交于 A，B 两点．‎ （i） 若直线 AF2 与 BF2 的斜率分别为 k1，k2，且 k1+k2=0，求证：直线 l 过定点，并求出该定点的坐标；（5 分）‎ （ii） 若直线 l 的斜率是直线 OA，OB 斜率的等比中项，求△OAB 面积的取值范围（6 分）．‎ 4. ‎（本题满分 16 分）已知函数，a∈R．‎ ‎（I）若 a=-1，求函数 f（x）的单调区间；（5 分）‎ ‎（Ⅱ）若 f（x）≥0 在 x∈[1，+∞）上恒成立，求正数 a 的取值范围；（5 分）‎ ‎（Ⅲ）证明： ．（6 分）‎ 第 4页，共 4页