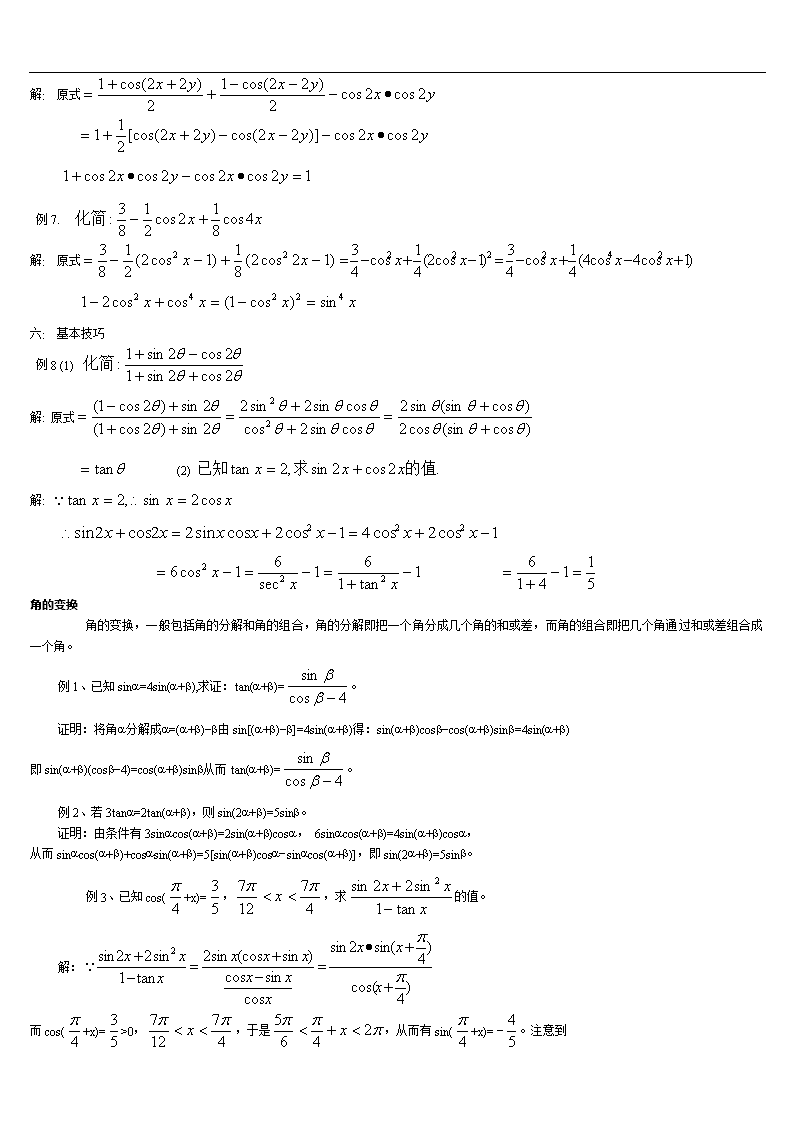高考数学专题复习（精选精讲）练习3-积化和差与和差化积公式的应用习题精选精讲 11页

三角函数式的化简 要求是:项数最少三角函数种类最少函数次数最低尽可能不带根号 能求值得要求出值.‎ ‎ 一: 定义法 例1. 化简 ‎ ‎ 解: 设点 ‎ ‎ ‎ 二: 弦切互化法 ‎ 例2. ‎ 解: 原式 ‎ ‎ 三: 变用公式 ‎ 例3. ‎ ‎ 解: 原式 ‎ ‎ 说明: 公式在解题中运用非常灵活.常常变形为 ‎ 来使用.‎ 四: 连锁反应法 ‎ 例5. ‎ 解: 原式 ‎=‎ 说明: 此题分子分母同乘以,从而连续逆用倍角公式,达到多次化角的目地.‎ 五: 升降次法 ‎ 例6. ‎ 解: 原式 ‎ ‎ ‎ ‎ ‎ 例7. ‎ 解: 原式 ‎ ‎ 六: 基本技巧 ‎ 例8 (1) ‎ 解: 原式 ‎ (2) ‎ 解: ‎ ‎ ‎ 角的变换 ‎ 角的变换，一般包括角的分解和角的组合，角的分解即把一个角分成几个角的和或差，而角的组合即把几个角通过和或差组合成一个角。‎ ‎ 例1、已知sina=4sin(a+b),求证：tan(a+b)=。‎ ‎ 证明：将角a分解成a=(a+b)-b由sin[(a+b)-b]=4sin(a+b)得：sin(a+b)cosb-cos(a+b)sinb=4sin(a+b)‎ 即sin(a+b)(cosb-4)=cos(a+b)sinb从而tan(a+b)=。‎ ‎ 例2、若3tana=2tan(a+b)，则sin(2a+b)=5sinb。‎ ‎ 证明：由条件有3sinacos(a+b)=2sin(a+b)cosa， 6sinacos(a+b)=4sin(a+b)cosa，‎ 从而sinacos(a+b)+cosasin(a+b)=5[sin(a+b)cosa-sinacos(a+b)]，即sin(2a+b)=5sinb。‎ ‎ 例3、已知cos(+x)=，，求的值。‎ ‎ 解：‎ 而cos(+x)=>0，，于是，从而有sin(+x)= -。注意到 cos2(+x)=2cos2(+x)-1=2()2-1= -sin2x=于是原式=。‎ ‎ 以上解题过程，紧紧抓住角的变捣，是灵活解题之关键，因此要注意分析思考角的关系，找出差异实现转化。‎ ‎ 例4、已知：a+bÎ(，p)，a-bÎ(0，)，且sin(a-b)=，cos(a+b)= -，求b。‎ ‎ 解：先求2b，而2b=(a+b)-(a-b)，由题可得：cos(a-b)=，sin(a+b)=，‎ ‎ cos2b=cos[(a+b)-(a-b)]=cos(a+b)cos(a-b)+sin(a+b)sin(a-b) = -·+·=‎ ‎ 又