数学卷·2018届云南省曲靖市沾益县第一中学高二上学期第四次质量检测（2016-12） 9页

高二年级第4次月考数学试卷 ‎（满分：150分；考试用时：120分钟）‎ 备注：考生必须在答题卡相应位置作答；在试卷上答题无效。‎ 一、选择题：（每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．直线的倾斜角是 （ ） ‎ A． B． C． D． ‎ ‎2．若一抛物线的顶点在原点，焦点为 ,在该抛物线的方程为 （ ）‎ ‎ A. B. C. D. ‎ 3. 命题“若，则或”的否命题是 （ ）‎ A. 若，则或 ‎ B. 若，则且 ‎ C. 若，则或 ‎ D. 若，则且 ‎4. 对于平面和两条不同的直线、,下列命题是真命题的是 （　　）‎ ‎ A. 若与所成的角相等,则 B. 若则 ‎ C. 若,则 D. 若,则 ‎5. 设函数f(x)在定义域内可导，y=f(x)的图象如下右图所示，则导函数y=f ¢(x)可能为（ ）‎ x y O ‎ ‎ ‎ A B C D 6. 一个四棱锥的底面为正方形，其三视图如图所示，‎ ‎ 则这个四棱锥的体积是 （ ）‎ ‎ A. B. ‎ ‎ C. D . 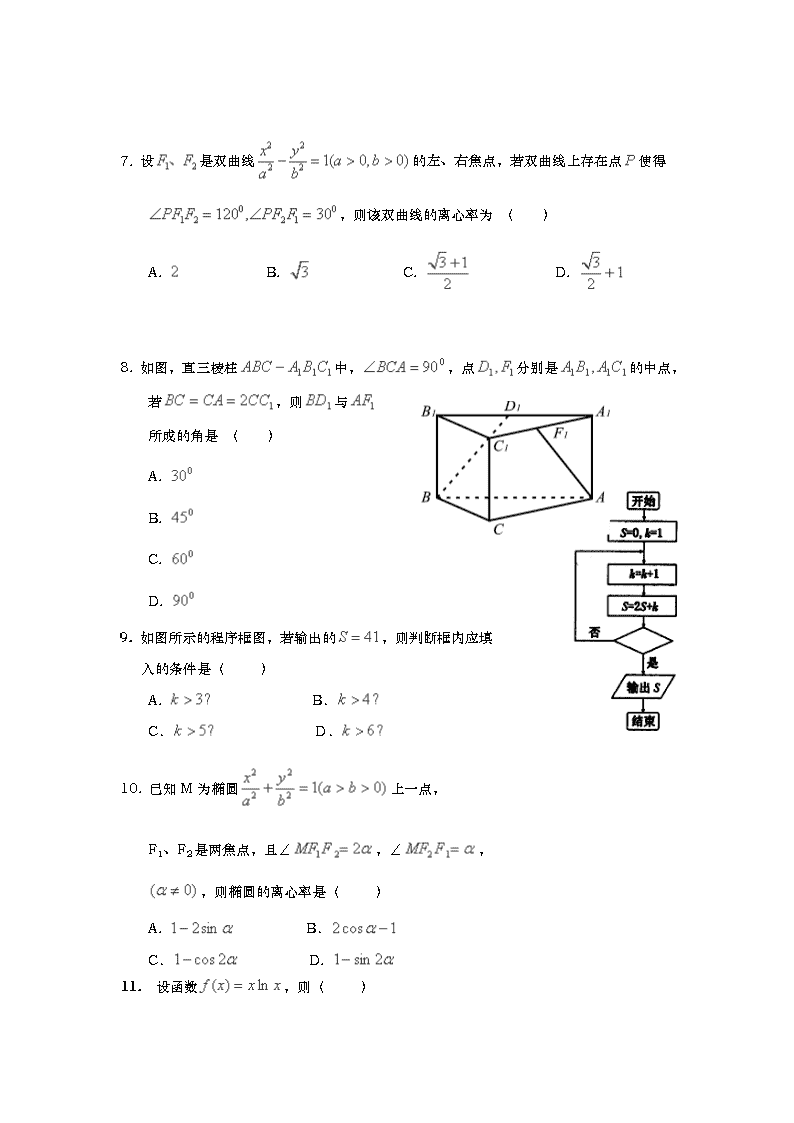‎ 6. 设是双曲线的左、右焦点，若双曲线上存在点使得 ‎ ，则该双曲线的离心率为 （ ）‎ A. B. C. D. ‎ 7. 如图，直三棱柱中，，点分别是的中点，‎ 若，则与 所成的角是 （ ） ‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎9. 如图所示的程序框图，若输出的，则判断框内应填 ‎ ‎ 入的条件是（ ）‎ ‎ A. B． ‎ ‎ C． D．‎ 10. 已知M为椭圆上一点，‎ F1、F2是两焦点，且∠，∠，‎ ‎，则椭圆的离心率是（ ）‎ A. B． ‎ C． D. ‎ ‎11. 设函数，则（ ）‎ ‎ A. 为的极小值点 B. 为的极小值点 C. 为的极大值点 D. 为的极大值点 12. 如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为 ‎ 96颗,以此试验数据为依据可以估计出椭圆的面积约为（ ）‎ A. 7.68 B. 8.68 ‎ C. 16.32 D. 17.32‎ 二、填空题：(本大题共4个小题，每小题5分，共20分)‎ ‎13. 若x、满足和，则的取值范围是________。‎ ‎14. 已知直线与直线平行，则值为___________。‎ ‎15. 把“二进制”数化为“五进制”数是 。 ‎ ‎16．（文科）函数恒过定点A，则A的坐标为              。‎ ‎(理科) = 。‎ 三、解答题：（本大题共6小题，共70分）解答应写出文字说明，证明过程或演算步骤。‎ ‎17.（本题10分）的内角所对的边分别为，向量 ‎ 与平行。‎ ‎ （Ⅰ）求； （Ⅱ）若求的面积。‎ ‎ ‎ 18． ‎（本小题共12分）已知等差数列的前项和为，等比数列满足，‎ ‎ ，。‎ ‎ （Ⅰ）求数列，的通项公式；‎ ‎ （Ⅱ）如果数列为递增数列，求数列的前项和。‎ ‎19. (本题12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:‎ 分组(重量)‎ 频数(个)‎ ‎5‎ ‎10‎ ‎20‎ ‎15‎ ‎ （1）根据频数分布表计算苹果的重量在的频率；‎ ‎ （2）用分层抽样的方法从重量在和的苹果中共抽取4个,其中重量在的有几个？‎ ‎（3）在(2)中抽出的4个苹果中,任取2个,求重量在和中各有1个的概率。‎ 20. ‎(本题12分)如图，在三棱锥中，，， ‎ ‎ BC平面PAC。‎ ‎ （Ⅰ）求证：； ‎ A P B C ‎ （Ⅱ）求三棱锥P-ABC的体积。‎ ‎ （Ⅲ）（理科做，文科不做）求二面角的正弦值。‎ 21. ‎(本题共12分)已知函数在处取得极值。‎ ‎ （1）求的值；‎ ‎ （2）若对恒成立，求的取值范围。‎ ‎22．(本题共12分)如图，椭圆＋＝1(a＞b＞0)的左、右焦点分别为F1 (－c,0)，F2(c,0)．‎ ‎ 已知点M 在椭圆上，且点M到两焦点距离之和4。‎ ‎（1）求椭圆的方程；‎ ‎（2）设与MO(O为坐标原点)垂直的直线交椭圆于 A，B（A，B不重合），求O·O的取值范围。‎ 沾益县2015━2016学年上学期学业水平评价 高二年级数学参考答案 一、选择题 ‎ 1. A 2. D 3. B 4. D 5. D 6. B 7. C 8. D 9. B 10. B 11. B 12. C 二、 填空题 ‎ 13. ［1，3］ ； 14.- 8 ‎ ‎ 15． 324(5) ； 16. 文（0,2） 理 2 ‎ 三、解答题 ‎17. (I)因为，所以，由正弦定理，‎ ‎ 得，‎ ‎ ，从而，由于，所以； 5分 ‎ ‎(II)解法一：由余又弦定理，得，代入数值求得，‎ ‎ 由面积公式得 ‎ 面积为.解法二：由正弦定理，得，从而又 由知，所以，由，计算得 ‎，所以面积为. 10分 ‎18. （Ⅰ）设等差数列的公差为，等比数列的公比为，则由题意得 ‎ ．代入得，解得或（舍）．‎ ‎ 所以．所以；或． 6分 ‎（Ⅱ）因为数列为递增数列，‎ ‎ 所以．所以，‎ ‎ ，相减得，‎ ‎ 所以． 12分 ‎19．解：(1)重量在的频率为：；……3分 ‎(2)若采用分层抽样的方法从重量在和的苹果中共抽取4个,则重量在的个数为：；…………6分 ‎(3)设在中抽取的一个苹果为,在中抽取的三个苹果分别为,从抽出的个苹果中,任取个共有,,,,,种情况. ……………9分 其中符合 “重量在和中各有一个”的情况共有3种;设“抽出的个苹果中,任取个,重量在和中各有一个”为事件,则事件的概率. ……………………………………12分 ‎20. 本题12分）解：（Ⅰ）取中点，连结．‎ ‎，．‎ ‎，． ‎ ‎，平面．‎ 平面， ．‎ ‎（Ⅱ）AB=AP=PB,PC=2，S△APC =2，VP-ABC=VB-APC=1/3S△APC*BC=4/3 ‎ A P B C E ‎（Ⅲ）（理科）取中点．连结．‎ ‎，‎ ‎,‎ 又，,‎ ‎．‎ 是二面角的平面角．…………9分 ‎,‎ 又,‎ ‎, ‎ ‎,,‎ 在,．‎ 二面角的正弦值为． ………………12分 ‎21.解：（1） 在处取得极值 ‎ ∴ ……4分 ‎ （2）由（1）得 ‎ ∵对恒成立， ‎ ‎ ∴对恒成立，‎ ‎ 即对恒成立， ……………6分 ‎ 令 ，‎ ‎ ，解得，（舍） ………8分 ‎ 在单调递减，单调递增 ‎ ‎ ，∴ ∴ ………12分 ‎22. 解：(1)∵‎2a＝4，∴ a＝2，又M在椭圆上，‎ ‎ ∴＋＝1，解得b2＝2，∴所求椭圆方程＋＝1.‎ ‎ (2)由题意知kMO＝，∴kAB＝－.‎ ‎ 设直线AB的方程为y＝－x＋m，联立方程组 ‎ 消去y，得13x2－4mx＋‎2m2‎－4＝0，‎ ‎ Δ＝(－‎4‎m)2－4×13×(‎2m2‎－4)＝8(‎12m2‎－‎13m2‎＋26)＞0，‎ ‎ ∴m2＜26，设A(x1，y1)，B(x2，y2)，‎ 由根与系数的关系得x1＋x2＝，x1x2＝，‎ ‎ 则O·O＝x1x2＋y1y2＝7x1x2－m(x1＋x2)＋m2‎ ‎ ＝∈.‎ ‎ ∴O·O的取值范围是.‎