- 652.50 KB
- 2021-06-07 发布
高二(16)班期末考试
数学试卷
一 .选择题:(本题共12小题,每小题5分)
1. 复数 (为虚数单位)的虚部为( )
A. B. C. D.
2. 已知集合,则=( )
A. B. C. D.
3. 下列选项中,说法正确的是( )
A.若,则
B. 向量 共线的充要条件是
C. 命题“”的否定是“”
D. 已知函数在区间上的图象是连续不断的,则命题“若 ,则在区间内至少有一个零点”的逆命题为假命题
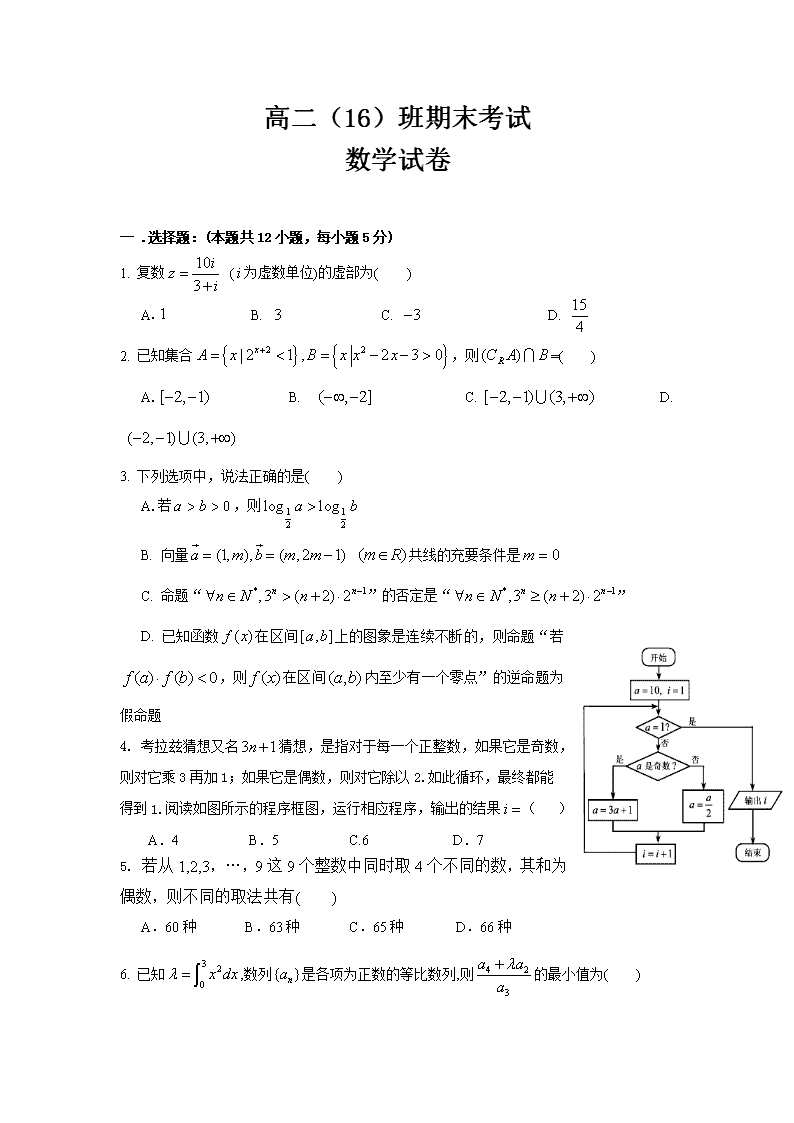
4. 考拉兹猜想又名猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果( )
A.4 B.5 C.6 D.7
5. 若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
A.60种 B.63种 C.65种 D.66种
6. 已知,数列是各项为正数的等比数列,则的最小值为( )
A. B. C. D.
7. 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则几何体的体积为( )
A. B. C. D.
8. 已知直线与函数的图象恰有三个不同的公共点,则实数的取值范围是( )
A. B. C. D.
9. 设关于的不等式组表示的平面区域内存在点,满足.则的取值范围是( )
A. B. C. D.
10. 已知为双曲线的左焦点,点为双曲线虚轴的一个顶点,过的直线与双曲线的一条渐近线在轴右侧的交点为,若,则此双曲线的离心率是( )
A. B. C. D.
11. 平行四边形中,,沿将四边形折起成直二面角,且,则三棱锥的外接球的表面积为( )
A. B. C. D.
12. 定义在上的可导函数满足,且,当时,不等式的解集为( )
A. B. C. D.
二、填空题:(本题共4小题,每小题5分)
13. 已知向量,的夹角为,且,,则 .
14. 将函数的图象向右平移个单位长度,所得图象关于点对称,则的最小值是 .
15. 已知数列满足:,函数,若,则的值是 .
16. 若方程有四个不同的实数根,且,则的取值范围是 .
三.解答题:(本题共小题.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分分)
已知a,b,c为△ABC的内角A,B,C的对边,满足=,函数f(x)=sin ωx(ω>0)在区间上单调递增,在区间上单调递减.
(1)证明:b+c=2a;
(2)若f=cos A,试判断△ABC的形状.
18. (本小题满分分)
张先生家住H小区,他工作在C科技园区,从家到公司上班的路上有L1, L2两条路线(如图所示),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,.
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯的次数X的数学期望;
(3)按照“遇到红灯的平均次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
19.(本小题满分分)
如图,在三棱柱中,,,为的中点,. (1)求证:平面平面;
(2)在线段(不含端点)上,是否存在点,使得二面角的余弦值为?若存在,求出的值,若不存在,说明理由。
19题图
20题图
20. (本小题满分分)
如图,椭圆的左焦点为,右焦点为,过的直线交椭圆于两点,的周长为8,且面积最大时,为正三角形。
(1) 求椭圆的方程;
(2) 设动直线与椭圆有且只有一个公共点,且与直线相交于点,试探究:①以为直径的圆与轴的位置关系?
②在坐标平面内是否存在定点,使得以为直径的圆恒过点?若存在,求出的坐标;若不存在,说明理由。
21. (本小题满分分)
设在点处的切线与直线垂直。
(1) 若对于任意的恒成立,求实数的取值范围;
(2) 设函数在上有且只有一个零点,求实数的取值范围。
请考生在第22、23题中任选一题作答,如果多做,则按所做第一题计分.
22. (本小题满分分) 选修4-4:坐标系与参数方程
在直角坐标标系中,已知曲线(为参数,),在以原点
为极点,轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线,曲线.
(1) 求曲线与的交点的直角坐标;
(2) 设分别为曲线,上的动点,求的最小值.
23. (本小题满分分) 选修4-5:不等式选讲
设函数,.
(1) 当时,解不等式:;
(2) 若关于的不等式的解集为,且两正数和满足,求证:
.