2018-2019学年新疆实验中学高一下学期期末考试数学试题（解析版） 17页

‎2018-2019学年新疆实验中学高一下学期期末考试数学试题 一、单选题 ‎1．直线（是参数）被圆截得的弦长等于（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】先消参数得直线普通方程，再根据垂径定理得弦长.‎ ‎【详解】‎ 直线（是参数），消去参数化为普通方程：．‎ 圆心到直线的距离，‎ ‎∴直线被圆截得的弦长.‎ 故选：D．‎ ‎【点睛】‎ 本题考查参数方程化普通方程以及垂径定理，考查基本分析求解能力，属基础题.‎ ‎2．设、、为平面，为、、直线，则下列判断正确的是（ ）‎ A．若，，，则 B．若，，，则 C．若，，，则 D．若，，，则 ‎【答案】D ‎【解析】根据线面、面面有关的定理，对四个选项逐一分析，由此得出正确选项.‎ ‎【详解】‎ A选项不正确，因为根据面面垂直的性质定理，需要加上：在平面内或者平行于，这个条件，才能判定.B选项不正确，因为可能平行于 ‎.C选项不正确，因为当时，或者.D选项正确，根据垂直于同一条直线的两个平面平行，得到，直线，则可得到.综上所述，本小题选D.‎ ‎【点睛】‎ 本小题主要考查空间线面、面面位置关系有关命题真假性的判断，属于基础题.‎ ‎3．如图，正方体的棱长为1，动点E在线段上, F，M分别是AD，CD的中点, 则下列结论中错误的是( )‎ A．‎ B．平面 C．三棱锥的体积为定值 D．存在点E，使得平面BEF//平面 ‎【答案】D ‎【解析】根据空间中的平行与垂直关系，和三棱锥的体积公式，对选项中的命题判断其真假性即可．‎ ‎【详解】‎ 对于A，连接AC，易知：故，正确；‎ 对于B，易知： ，‎ ‎,故平面，正确；‎ 对于C，三棱锥的体积等于三棱锥的体积,此时E点到平面BCF的距离为1，底面积为，故体积为定值，正确；‎ 对于D,BF与CD相交，即平面BEF与平面始终有公共点，故二者相交，错误；‎ 故选：D ‎【点睛】‎ 本题考查了空间中的线面位置关系的判断和棱锥的体积计算问题，涉及到三棱锥的体积为定值问题，要考虑到动点（棱锥的顶点）在直线上，而直线与平面（棱锥的底面）平行，这样不论动点怎样移动，棱锥的高都不变，底面积为定值，高为定值，体积就是定值，考查学生的空间想象能力，是综合题．‎ ‎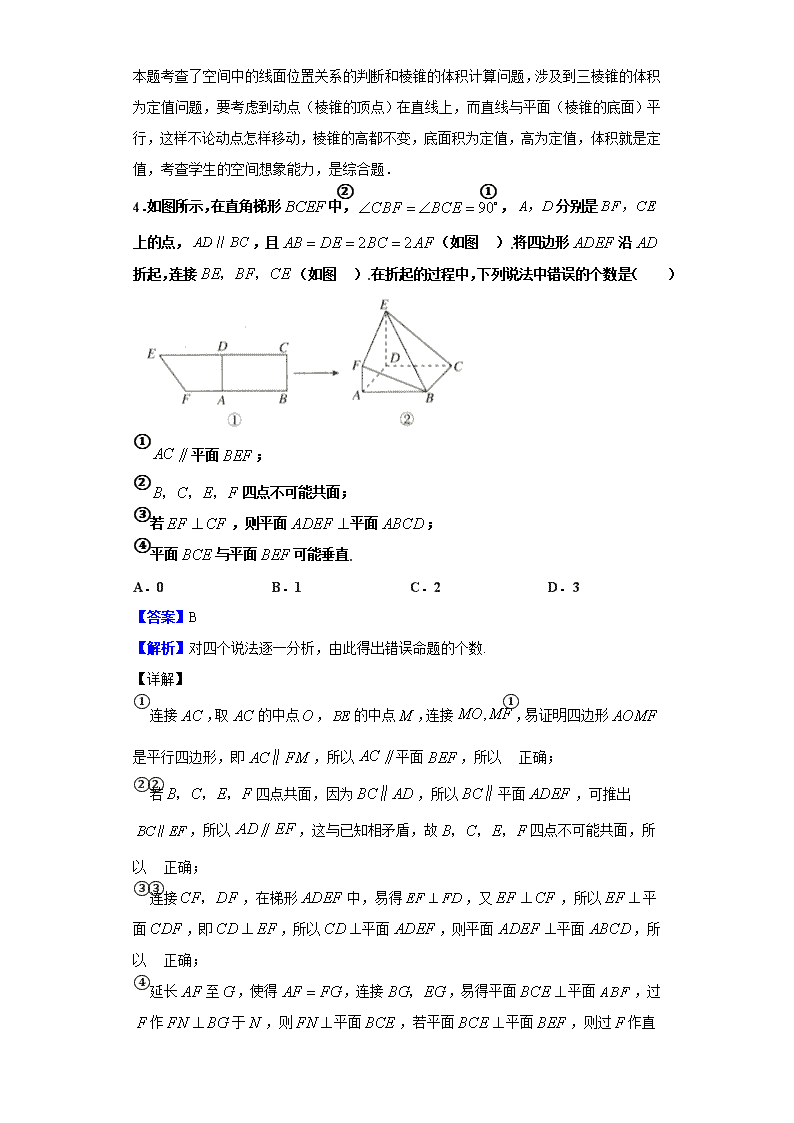4．如图所示，在直角梯形中，，分别是上的点，，且（如图①）.将四边形沿折起，连接（如图②）.在折起的过程中，下列说法中错误的个数是（ ）‎ ‎①平面；‎ ‎②四点不可能共面；‎ ‎③若，则平面平面；‎ ‎④平面与平面可能垂直.‎ A．0 B．1 C．2 D．3‎ ‎【答案】B ‎【解析】对四个说法逐一分析，由此得出错误命题的个数.‎ ‎【详解】‎ ‎①连接，取的中点，的中点，连接，易证明四边形是平行四边形，即，所以平面，所以①正确；‎ ‎②若四点共面，因为，所以平面，可推出，所以，这与已知相矛盾，故四点不可能共面，所以②正确；‎ ‎③连接，在梯形中，易得，又，所以平面，即，所以平面，则平面平面，所以③正确；‎ ‎④延长至，使得，连接，易得平面平面，过作于，则平面，若平面平面，则过 作直线与平面垂直，其垂足在上，前后矛盾，故④错误.综上所述，一共有个说法错误.故选B.‎ ‎【点睛】‎ 本小题主要考查线面平行、四点共面、面面垂直等命题的真假性的判断，属于中档题.‎ ‎5．直线l：与圆C：交于A，B两点，则当弦AB最短时直线l的方程为 A． B．‎ C． D．‎ ‎【答案】A ‎【解析】先求出直线经过的定点，再求出弦AB最短时直线l的方程.‎ ‎【详解】‎ 由题得，‎ 所以直线l过定点P.‎ 当CP⊥l时，弦AB最短.‎ 由题得,‎ 所以.‎ 所以直线l的方程为.‎ 故选：A ‎【点睛】‎ 本题主要考查直线过定点问题，考查直线方程的求法，考查直线和圆的位置关系，意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ ‎6．已知某圆柱的底面周长为12，高为2，矩形是该圆柱的轴截面，则在此圆柱侧面上，从到的路径中，最短路径的长度为（ ）‎ A． B． C．3 D．2‎ ‎【答案】A ‎【解析】由圆柱的侧面展开图是矩形，利用勾股定理求解．‎ ‎【详解】‎ 圆柱的侧面展开图如图，‎ 圆柱的侧面展开图是矩形，且矩形的长为12，宽为2，‎ 则在此圆柱侧面上从到的最短路径为线段，‎ ‎.‎ 故选：A．‎ ‎【点睛】‎ 本题考查圆柱侧面展开图中的最短距离问题，是基础题．‎ ‎7．下列命题中正确的是（　　）‎ A．如果两条直线都平行于同一个平面，那么这两条直线互相平行 B．过一条直线有且只有一个平面与已知平面垂直 C．如果一条直线平行于一个平面内的一条直线，那么这条直线平行于这个平面 D．如果两条直线都垂直于同一平面，那么这两条直线共面 ‎【答案】D ‎【解析】利用定理及特例法逐一判断即可。‎ ‎【详解】‎ 解：如果两条直线都平行于同一个平面，那么这两条直线相交、平行或异面，故A不正确；‎ 过一条直线有且只有一个平面与已知平面垂直，不正确．‎ 反例：如果该直线本身就垂直于已知平面的话，‎ 那么可以找到无数个平面与已知平面垂直，故B不正确；‎ 如果这两条直线都在平面内且平行，那么这直线不平行于这个平面，故C不正确；‎ 如果两条直线都垂直于同一平面，则这两条直线平行，‎ 所以这两条直线共面，故D正确．‎ 故选：D．‎ ‎【点睛】‎ 本题主要考查了线线平行的判定，面面垂直的判定，线面平行的判定，线面垂直的性质，考查空间思维能力，属于中档题。‎ ‎8．一个几何体的三视图如图所示，则几何体的体积是( )‎ A． B． C． D．1‎ ‎【答案】C ‎【解析】由三视图知几何体为三棱锥，且三棱锥的高为，底面是直角边长分别为1，的直角三角形，代入体积公式计算可得答案．‎ ‎【详解】‎ 解：由三视图知几何体为三棱锥，且三棱锥的高为，‎ 底面是直角边长分别为1，的直角三角形，‎ ‎∴三棱柱的体积V．‎ 故选：C．‎ ‎【点睛】‎ 本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．‎ ‎9．若一个正四棱锥的侧棱和底面边长相等，则该正四棱锥的侧棱和底面所成的角为（ ）‎ A．30° B．45° C．60° D．90°‎ ‎【答案】B ‎【解析】正四棱锥 ，连接底面对角线 ，在中，为侧棱与地面所成角，通过边的关系得到答案.‎ ‎【详解】‎ 正四棱锥 ，连接底面对角线， ，易知为等腰直角三角形.‎ 中点为 ，又正四棱锥知：底面 ‎ 即 为所求角为 ，答案为B ‎【点睛】‎ 本题考查了线面夹角的计算，意在考察学生的计算能力和空间想象力.‎ ‎10．l：与两坐标轴所围成的三角形的面积为 A．6 B．1 C． D．3‎ ‎【答案】D ‎【解析】先求出直线与坐标轴的交点，再求三角形的面积得解.‎ ‎【详解】‎ 当x=0时，y=2,‎ 当y=0时，x=3,‎ 所以三角形的面积为.‎ 故选：D ‎【点睛】‎ 本题主要考查直线与坐标轴的交点的坐标的求法，意在考查学生对该知识的理解掌握水平和分析推理能力.‎ ‎11．l：的斜率为 A．﹣2 B．2 C． D．‎ ‎【答案】B ‎【解析】先化成直线的斜截式方程即得直线的斜率.‎ ‎【详解】‎ 由题得直线的方程为y=2x,‎ 所以直线的斜率为2.‎ 故选：B ‎【点睛】‎ 本题主要考查直线斜率的求法，意在考查学生对该知识的理解掌握水平和分析推理能力.‎ ‎12．一个正四棱锥的底面边长为2，高为，则该正四棱锥的全面积为 A．8 B．12 C．16 D．20‎ ‎【答案】B ‎【解析】先求侧面三角形的斜高，再求该正四棱锥的全面积.‎ ‎【详解】‎ 由题得侧面三角形的斜高为，‎ 所以该四棱锥的全面积为.‎ 故选：B ‎【点睛】‎ 本题主要考查几何体的边长的计算和全面积的求法，意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ 二、填空题 ‎13．已知两条直线, 将圆及其内部划分成三个部分, 则的取值范围是_______；若划分成的三个部分中有两部分的面积相等, 则的取值有_______种可能.‎ ‎【答案】 3 ‎ ‎【解析】易知直线过定点，再结合图形求解.‎ ‎【详解】‎ 依题意得直线过定点，如图： ‎ ‎ ‎ 若两直线将圆分成三个部分，‎ 则直线必须与圆相交于图中阴影部分.‎ 又，‎ 所以的取值范围是；‎ 当直线位于时，‎ 划分成的三个部分中有两部分的面积相等.‎ ‎【点睛】‎ 本题考查直线和圆的位置关系的应用，直线的斜率，结合图形是此题的关键.‎ ‎14．已知直线与圆交于两点，若，则____.‎ ‎【答案】‎ ‎【解析】根据点到直线距离公式与圆的垂径定理求解.‎ ‎【详解】‎ 圆的圆心为，半径为，‎ 圆心到直线的距离： ，‎ 由得，‎ 解得.‎ ‎【点睛】‎ 本题考查直线与圆的应用.此题也可联立圆与直线方程，消元后用弦长公式求解.‎ ‎15．某几何体是由一个正方体去掉一个三棱柱所得，其三视图如图所示.如果网格纸上小正方形的边长为1，那么该几何体的体积是___‎ ‎【答案】6‎ ‎【解析】先作出几何体图形，再根据几何体的体积等于正方体的体积减去三棱柱的体积计算.‎ ‎【详解】‎ 几何体如图所示：‎ ‎ ‎ 去掉的三棱柱的高为2，底面面积是正方体底面积的 ，‎ 所以三棱柱的体积： ‎ 所以几何体的体积：‎ ‎【点睛】‎ 本题考查三视图与几何体的体积.关键是作出几何体的图形，方法：先作出正方体的图形，再根据三视图“切”去多余部分.‎ ‎16．已知圆锥的轴截面是边长为2的正三角形，则这个圆锥的表面积等于______．‎ ‎【答案】‎ ‎【解析】根据圆锥轴截面的定义结合正三角形的性质，可得圆锥底面半径长和高的大小，由此结合圆锥的表面积公式，能求出结果．‎ ‎【详解】‎ ‎∵圆锥的轴截面是正三角形，边长等于2‎ ‎∴圆锥的高，‎ 底面半径.‎ ‎∴这个圆锥的表面积：‎ ‎.‎ 故答案为：．‎ ‎【点睛】‎ 本题给出圆锥轴截面的形状，求圆锥的表面积，着重考查了等边三角形的性质和圆锥的轴截面等基础知识，考查运算求解能力，是基础题．‎ 三、解答题 ‎17．如图，在多面体中，平面平面，四边形为正方形，四边形为梯形，且，，．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面； ‎ ‎（Ⅲ）在线段上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由.‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）见解析；（Ⅲ）见解析 ‎【解析】（Ⅰ）转化为证明；（Ⅱ）转化为证明，；（Ⅲ）根据线面平行的性质定理.‎ ‎【详解】‎ ‎（Ⅰ）因为四边形为正方形，所以，由于平面，‎ 平面，所以平面.‎ ‎（Ⅱ）因为四边形为正方形，‎ 所以.平面平面，‎ 平面平面，‎ 所以平面.所以.‎ 取中点，连接.由，，，‎ 可得四边形为正方形.‎ 所以.所以.所以.‎ 因为，所以平面. ‎ ‎（Ⅲ）存在，当为的中点时，平面，此时.‎ ‎ 证明如下：‎ 连接交于点，由于四边形为正方形，‎ 所以是的中点，同时也是的中点.‎ 因为，又四边形为正方形， ‎ 所以，‎ 连接，所以四边形为平行四边形.‎ 所以.又因为平面，平面，‎ 所以平面. ‎ ‎【点睛】‎ 本题考查空间线面的关系.线面关系的证明要紧扣判定定理，转化为线线关系的证明.‎ ‎18．己知点，直线l与圆C：（x一1)2＋（y一2）2＝4相交于A，B两点，且OA⊥OB．‎ ‎（1）若直线OA的方程为y＝一3x，求直线OB被圆C截得的弦长；‎ ‎（2）若直线l过点（0，2），求l的方程．‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）根据题意，求得直线OB的方程，利用点到直线的距离公式求得圆心到直线OB的距离，之后应用圆中的特殊三角形，求得弦长；‎ ‎（2）根据题意，可判断直线的斜率是存在的，设出其方程，与圆的方程联立，得到两根和与两根积，根据OA⊥OB，利用向量数量积等于零得到所满足的等量关系式，求得结果.‎ ‎【详解】‎ ‎（1）因为直线OA的方程为，，‎ 所以直线OB的方程．‎ 从而圆心到直线OB的距离为：‎ 所以直线OB被团C截得的弦长为：．‎ ‎（2）依题意，直线l的斜率必存在，不妨设其为k，则l的方程为，‎ 又设，．‎ 由得，‎ 所以，．‎ 从而．‎ 所以． ‎ 因为，所以，即，解得．‎ 所以l的方程为． ‎ ‎【点睛】‎ 该题考查的是有关直线与圆的问题，涉及到的知识点有两直线垂直的条件，直线被圆截得的弦长，直线方程的求解，属于简单题目.‎ ‎19．已知圆经过，，三点．‎ ‎(1)求圆的标准方程；‎ ‎(2)若过点N 的直线被圆截得的弦AB的长为，求直线的倾斜角．‎ ‎【答案】(1) (2) 30°或90°．‎ ‎【解析】‎ ‎（1）解法一：将圆的方程设为一般式，将题干三个点代入圆的方程，解出相应的参数值，即可得出圆的一般方程，再化为标准方程；‎ 解法二：求出线段和的中垂线方程，将两中垂线方程联立求出交点坐标，即为圆心坐标，然后计算为圆的半径，即可写出圆的标准方程；‎ ‎（2）先利用勾股定理计算出圆心到直线的距离为，并对直线的斜率是否存在进行分类讨论：一是直线的斜率不存在，得出直线的方程为，验算圆心到该直线的距离为；‎ 二是当直线的斜率存在时，设直线的方程为，并表示为一般式，利用圆心到直线的距离为得出关于的方程，求出的值。结合前面两种情况求出直线的倾斜角。‎ ‎【详解】‎ ‎（1）解法一：设圆的方程为， ‎ 则 ∴ ‎ 即圆为，‎ ‎∴圆的标准方程为； ‎ 解法二：则中垂线为,中垂线为， ‎ ‎∴圆心满足∴， ‎ 半径， ‎ ‎∴圆的标准方程为．‎ ‎（2）①当斜率不存在时，即直线到圆心的距离为1，也满足题意，‎ 此时直线的倾斜角为90°，‎ ‎②当斜率存在时，设直线的方程为， ‎ 由弦长为4，可得圆心 到直线的距离为， ‎ ‎， ‎ ‎∴，此时直线的倾斜角为30°， ‎ 综上所述，直线的倾斜角为30°或90°．‎ ‎【点睛】‎ 本题考查圆的方程以及直线截圆所得弦长的计算，在求直线与圆所得弦长的计算中，问题的核心要转化为弦心距的计算，弦心距的计算主要有以下两种方式：一是利用勾股定理计算，二是利用点到直线的距离公式计算圆心到直线的距离。‎ ‎20．如图，在三棱柱中，、分别是棱，的中点，求证：‎ ‎（1）平面；‎ ‎（2）平面平面．‎ ‎【答案】（1）见证明；（2）见证明 ‎【解析】（1）设与的交点为，连结，证明，再由线面平行的判定可得平面； ‎ ‎（2）由为线段的中点，点是的中点，证得四边形为平行四边形，得到，进一步得到平面．再由平面，结合面面平行的判定可得平面平面．‎ ‎【详解】‎ 证明：（1）设与的交点为，连结，‎ ‎∵四边形为平行四边形，∴为中点，‎ 又是的中点，∴是三角形的中位线，则，‎ 又∵平面，平面，‎ ‎∴平面；‎ ‎（2）∵为线段的中点，点是的中点，‎ ‎∴且，则四边形为平行四边形，‎ ‎∴，‎ 又∵平面，平面，‎ ‎∴平面．‎ 又平面，，且平面，平面，‎ ‎∴平面平面．‎ ‎【点睛】‎ 本题考查直线与平面，平面与平面平行的判定，考查空间想象能力与思维能力，是中档题．‎ ‎21．已知圆的圆心在轴上，且经过点，．‎ ‎（Ⅰ）求线段AB的垂直平分线方程；‎ ‎（Ⅱ）求圆的标准方程；‎ ‎（Ⅲ）过点的直线与圆相交于、两点，且，求直线的方程．‎ ‎【答案】（Ⅰ）；（Ⅱ）；（Ⅲ）或.‎ ‎【解析】（Ⅰ）利用垂直平分关系得到斜率及中点，从而得到结果；‎ ‎（Ⅱ）设圆的标准方程为，结合第一问可得结果；‎ ‎（Ⅲ）由题意可知：圆心到直线的距离为1，分类讨论可得结果.‎ ‎【详解】‎ 解：（Ⅰ） 设的中点为，则．‎ 由圆的性质，得，所以，得. ‎ 所以线段的垂直平分线的方程是. ‎ ‎(II) 设圆的标准方程为，其中，半径为（）.‎ 由圆的性质，圆心在直线上，化简得．‎ 所以 圆心， ‎ ‎， ‎ 所以 圆的标准方程为．‎ ‎(III) 由(I)设为中点，则，得．‎ 圆心到直线的距离.‎ ‎(1) 当的斜率不存在时，，此时，符合题意. ‎ ‎(2) 当的斜率存在时，设，即，‎ 由题意得，解得：．‎ 故直线的方程为，即．‎ 综上直线的方程或．‎ ‎【点睛】‎ 圆内一点为弦的中点时，则此点与圆心的连线和弦所在的直线垂直；解决圆的弦长有关问题，注意弦长一半、弦心距、半径构成的直角三角形的三边的勾股数之间的关系。‎