- 1.48 MB
- 2021-06-05 发布
文科数学试卷
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,集合,则( )
A. B. C. D.
2.在复平面中,复数的共轭复数,则对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.在等差数列中,已知,且公差,则其前项和取最小值时的的值为( )
A. B.或 C. D.
4.下列命题正确的是( )
A.存在,使得的否定是:不存在,使得
B.对任意,均有的否定是:存在,使得
C.若,则或的否命题是:若,则或
D.若为假命题,则命题与必一真一假
5.在平面直角坐标系中,向量,,若,,三点能构成三角形,则( )
A. B. C. D.
6.设函数,则“函数在上存在零点”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分且必要条件 D.既不充分也不必要条件
7.若,满足约束条件,则的范围是( )
A. B. C. D.
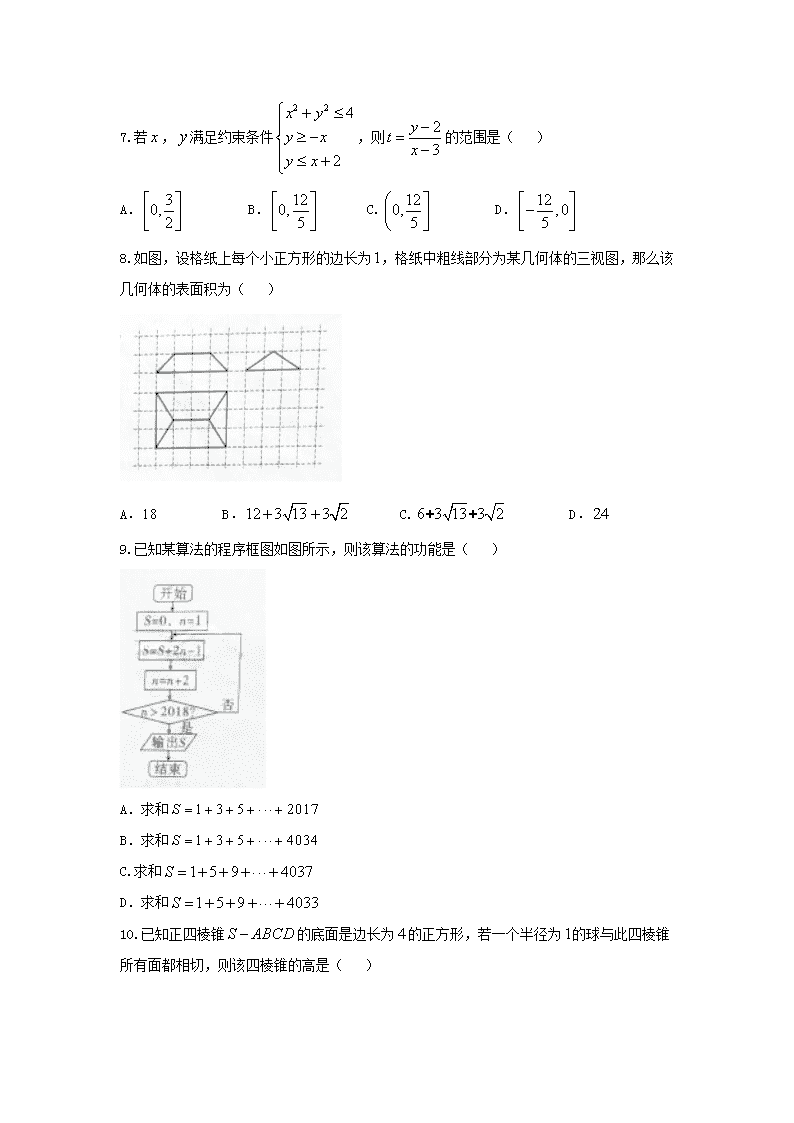
8.如图,设格纸上每个小正方形的边长为,格纸中粗线部分为某几何体的三视图,那么该几何体的表面积为( )
A. B. C. D.
9.已知某算法的程序框图如图所示,则该算法的功能是( )
A.求和
B.求和
C.求和
D.求和
10.已知正四棱锥的底面是边长为的正方形,若一个半径为的球与此四棱锥所有面都相切,则该四棱锥的高是( )
A. B. C. D.
11.已知为坐标原点,设,分别是双曲线的左、右焦点,点为双曲线左支上任一点,过点作的平分线的垂线,垂足为,若,则双曲线的离心率是( )
A. B. C. D.
12.已知是定义在上的奇函数,满足,当时,,则函数在区间上所有零点之和为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.在中,角,,的对边分别为,,,若,,,,则角的大小为 .
14.若圆与双曲线:的渐近线相切,则双曲线的渐近线方程是 .
15.设函数若且,,则,,取值范围分别是 .
16.已知函数,且点满足条件,若点关于直线:的对称点是,则线段的最小值是 .
三、解答题
(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知的内角,,所对的边分别是,,且,;等差数列的公差,.
(I)若角及数列的通项公式;
(II)若数列满足,求数列的前项和.
18.某市初三毕业生参加中考要进行体育测试,某实验中学初三(8)班的一次体育测试成绩的茎叶图和频率分布直方图都受到不同程度的涂黑,但可见部分如图,据此解答如下问题.
(I)求全班人是及中位数,并重新画出频率直方图;
(II)若要从分数在,之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在之间的概率.
19.如图,,为圆柱的母线,是底面圆的直径,是的中点.
(I)问:上是否存在点使得平面?请说明理由;
(II)在(I)的条件下,若平面,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥外会有
被捕的危险,求小鱼被捕的概率.
20.已知,,,直线,的斜率之积为.
(I)求顶点的轨迹方程;
(II)设动直线:,点关于直线的对称点为,且点在曲线上,求的取值范围.
21.已知函数,且,.
(I)设,求的单调区间及极值;
(II)证明:函数的图象在函数的图象的上方.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线的参数方程为(为参数),点是曲线上的一动点,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线的方程为.
(I)求线段的中点的轨迹的极坐标方程;
(II)求曲线上的点到直线的距离的最大值.
23.选修4-5:不等式选讲
设函数.
(I)作出函数的图象并求其值域;
(II)若,且,求的最大值.
贵阳第一中学2018届高考适应性月考卷(四)
理科数学参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
C
C
C
B
C
A
D
D
A
【解析】
1.,,图中阴影部分表示,故选B.
2.因为,所以,所以
,故选D.
3.若,则,且,解得或,∴“”是“”的充分不必要条件,故选A.
4.分别设甲、乙两贫困户获得扶持资金为事件A,B,,,“这两户中至少有一户获得扶持资金”的对立事件是“这两户都没有获得扶持资金”,概率为,所以这两户中至少有一户获得扶持资金的概率为,故选C.
5.设向量与的夹角为,由得,所以,所以,∵,∴,故选C.
6.将函数的图象上所有点的横坐标伸长到原来的倍,再向右平移个单位长度,得到函数的图象,所以,令
,得,,故选C.
7.由得,设,则,所以在R上是增函数, 且.不等式可化为,即,∴,故选B.
8.如图1所示,设,则,分别过,作准线的垂线,垂足分别为,,由抛物线的定义知,,,再过作的垂线,垂足为,则,所以,则,故选C.
图1
9.由三视图可知,该几何体是由正方体截去四个角后所得的正三棱锥,设正方体的棱长为,则该三棱锥的体积为,∴,因为该三棱锥的外接球就是正方体的外接球,∴该三棱锥的外接球的直径,所以该三棱锥的外接球的表面积为,故选A.
10.不妨设,由双曲线的定义,,又,联立解得,,,所以
,则△为直角三角形,,△的面积为
,所以,故选D.
11.,运行该程序得,当时,,不成立,继续循环;,,成立,循环结束,输出的,故选D.
12.由题意,问题等价于方程在上有两个解,即方程在上有两个解. 设,则,所以当时,,单调递减;当时,,单调递增;于是有最小值为,又,,,由图可知,若方程在上有两个解,则,所以,故选A.
二、填空题(本大题共4小题,每小题5分,共20分)
题号
13
14
15
16
答案
③④
【解析】
13.的展开式的通项.令,不合题意,舍去;令,得,所以的展开式中的系数是,得(舍负),所以.根据的几何意义是以原点为圆心,为半径的圆面积的,所以.
14.由约束条件作出可行域,如图2所示.表示可行域内的点到原点距离的平方,由图可知,.
15.∵,∴,
又,∴,所以且,故对任意,都有,∴.
16.画出函数的图象,如图3,由此判断③,④正确.
三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
17. (Ⅰ)证明:由,得,
由正弦定理,化简得,
根据余弦定理,
∵,∴,
又,∴,所以角A,C,B成等差数列.
(Ⅱ)解:根据余弦定理得,
∴,当且仅当时“”成立,
则△的面积为,
所以△面积的最大值为.
18. 解:(Ⅰ)由已知得,,,根据参考公式和数据得
,
∴,
∴关于的线性回归方程为.
(Ⅱ),
∵,∴对数函数回归模型更合适,
当万元时,预测A城市的销售额为万元.
19.
(Ⅰ)证明:∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴BC=DC,∠ADC=∠BCD=120°,∴∠CDB=30°,
∴∠ADB=90°,即BD⊥AD.
又AE⊥BD,=A,∴BD⊥平面AED,
又BD平面ABCD,∴平面AED⊥平面ABCD.
如图4,
过E作EG⊥AD于G,则EG⊥平面ABCD,
又FC⊥平面ABCD,∴FC∥EG.
又EG平面AED,FC平面AED,
∴FC∥平面AED.
(Ⅱ)解:如图5,
连接AC,由(Ⅰ)知AC⊥BC,
∵FC⊥平面ABCD,
∴CA,CB,CF两两垂直.
以C为原点,建立空间直角坐标系C−xyz.
设BC,则AC,AB,
,,,
,∴,
,.
设平面BDF的法向量为,
则 即
令,则,,则.
设直线AF与平面BDF所成角为,则,
故直线AF与平面BDF所成角的余弦值为.
20. 解:(Ⅰ)以原点为圆心,椭圆的短轴长为直径的圆的方程为,
由题意,,所以.
∵点在椭圆上,∴,解得,
∴椭圆C的方程为.
(Ⅱ)由,
根据椭圆定义,,所以,
于是求△内切圆面积的最大值即为求△面积的最大值.
设直线l的方程为,,,则
消去得,所以,.
因为,点到直线的距离为,
所以△的面积为.
令,则.
∵在上单调递增,∴当时,取得最大值为3,
此时,直线l的方程为,
内切圆的半径为,所以内切圆面积的最大值为.
21. 解:(Ⅰ)若,则,,
由得;由得,
所以的单调递增区间是,单调递减区间是.
(Ⅱ),所以当时,,单调递减;
当时,,单调递增,
又,,所以在上的最大值为.
由题意,若对任意的,都有成立,
即对任意的,都有恒成立,即恒成立,
即对任意的恒成立,所以.
设,,则,,
所以在上单调递减,则,
所以在上单调递减,又,
所以当时,,单调递增;
当时,,单调递减,
∴在上的最大值为,∴,
所以的取值范围是.
22.【选修4−4:坐标系与参数方程】
解:(Ⅰ)设线段的中点的坐标为,
由中点坐标公式得(为参数),
消去参数得的轨迹的直角坐标方程为,
由互化公式可得点的轨迹的极坐标方程为.
(Ⅱ)由直线的极坐标方程为,得,
所以直线的直角坐标方程为,
曲线的普通方程为,它表示以为圆心,2为半径的圆,
则圆心到直线的距离为,所以直线与圆相离,
故曲线上的点到直线的距离的最大值为.
23.【选修4−5:不等式选讲】
解:(Ⅰ)由
如图6所示,
值域.
(Ⅱ)由(Ⅰ)知,
∵
∴∴的最大值为,
当且仅当时,等号成立.