- 197.50 KB
- 2021-06-05 发布
专题六 第4讲 算法初步、复数
课时训练提能
[限时45分钟,满分75分]
一、选择题(每小题4分,共24分)
1.(2012·东莞模拟)复数的虚部是
A.-i B.-i
C.-1 D.-
解析 ==-i,故其虚部为-.
答案 D
2.(2012·芜湖模拟)在复平面内,与复数对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ==-i,故复数对应的点位于第四象限.
答案 D
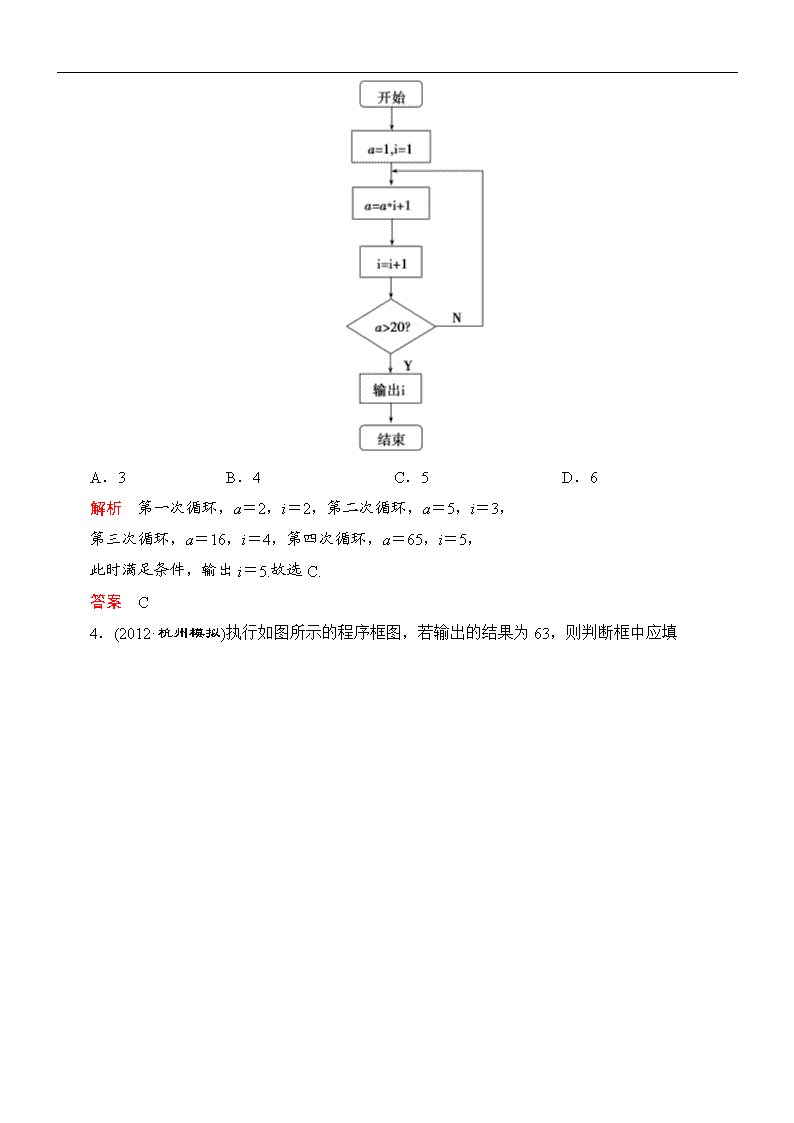
3.(2012·衡水模拟)阅读下边的程序框图,运行相应的程序,则输出i的值为
A.3 B.4 C.5 D.6
解析 第一次循环,a=2,i=2,第二次循环,a=5,i=3,
第三次循环,a=16,i=4,第四次循环,a=65,i=5,
此时满足条件,输出i=5.故选C.
答案 C
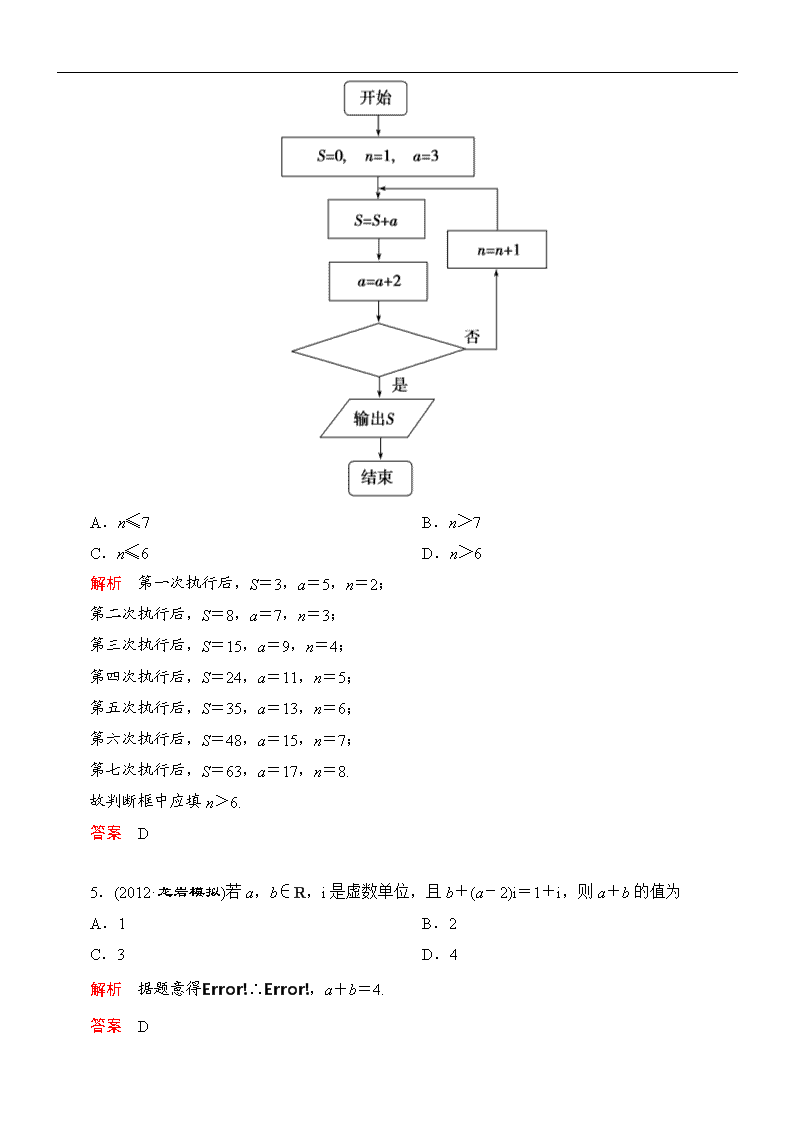
4.(2012·杭州模拟)执行如图所示的程序框图,若输出的结果为63,则判断框中应填
A.n≤7 B.n>7
C.n≤6 D.n>6
解析 第一次执行后,S=3,a=5,n=2;
第二次执行后,S=8,a=7,n=3;
第三次执行后,S=15,a=9,n=4;
第四次执行后,S=24,a=11,n=5;
第五次执行后,S=35,a=13,n=6;
第六次执行后,S=48,a=15,n=7;
第七次执行后,S=63,a=17,n=8.
故判断框中应填n>6.
答案 D
5.(2012·龙岩模拟)若a,b∈R,i是虚数单位,且b+(a-2)i=1+i,则a+b的值为
A.1 B.2
C.3 D.4
解析 据题意得∴,a+b=4.
答案 D
6.执行如图所示的程序框图,如果输入的n是4,则输出的p的值是
A.8 B.5
C.3 D.2
解析 由题知,第一次进入循环,满足1<4,循环后p=1,s=1,t=1,k=2;
第二次进入循环,满足2<4,循环后p=2,s=1,t=2,k=3;
第三次进入循环,满足3<4,循环后p=3,s=2,t=3,k=4,
因为4=4,不满足题意,所以循环结束.
输出p的值为3,故选C.
答案 C
二、填空题(每小题5分,共15分)
7.(2012·葫芦岛模拟)若复数(1+ai)(2+i)=3-i,则实数a的值为________.
解析 ∵(1+ai)(2+i)=2-a+(2a+1)i=3-i,
∴,∴a=-1.
答案 -1
8.若复数z同时满足z-=2i,=iz(i为虚数单位),
则z=________.
解析 把=iz代入z-=2i,得z-iz=2i,
即(1-i)z=2i,
∴z====-1+i.
答案 -1+i
9.如图是一个算法的程序框图,执行该程序后输出的W的值为________.
解析 第一次循环后,S=1,T=3;
第二次循环后,S=8,T=5;
第三次循环后,S=17≥10,循环结束.
则输出的W的值为17+5=22.
答案 22
三、解答题(每小题12分,共36分)
10.已知复数z1满足(z1-2)(1+i)=1-i(i为虚数单位),复数z2的虚部为2,且z1·z2是实数,求z2.
解析 (z1-2)(1+i)=1-i⇒z1=2-i.
设z2=a+2i,a∈R,则z1·z2=(2-i)(a+2i)=(2a+2)+(4-a)i.
∵z1·z2∈R,∴a=4.∴z2=4+2i.
11.画出计算S=1·22+2·23+3·24+…+10·211的值的程序框图.
解析 如图所示:
12.对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.
观测次数i
1
2
3
4
5
6
7
8
观测数据ai
40
41
43
43
44
46
47
48
在上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中是这8个数据的平均数),求输出的S的值.
解析 根据题中数据可得=44,
由程序框图得S==7.