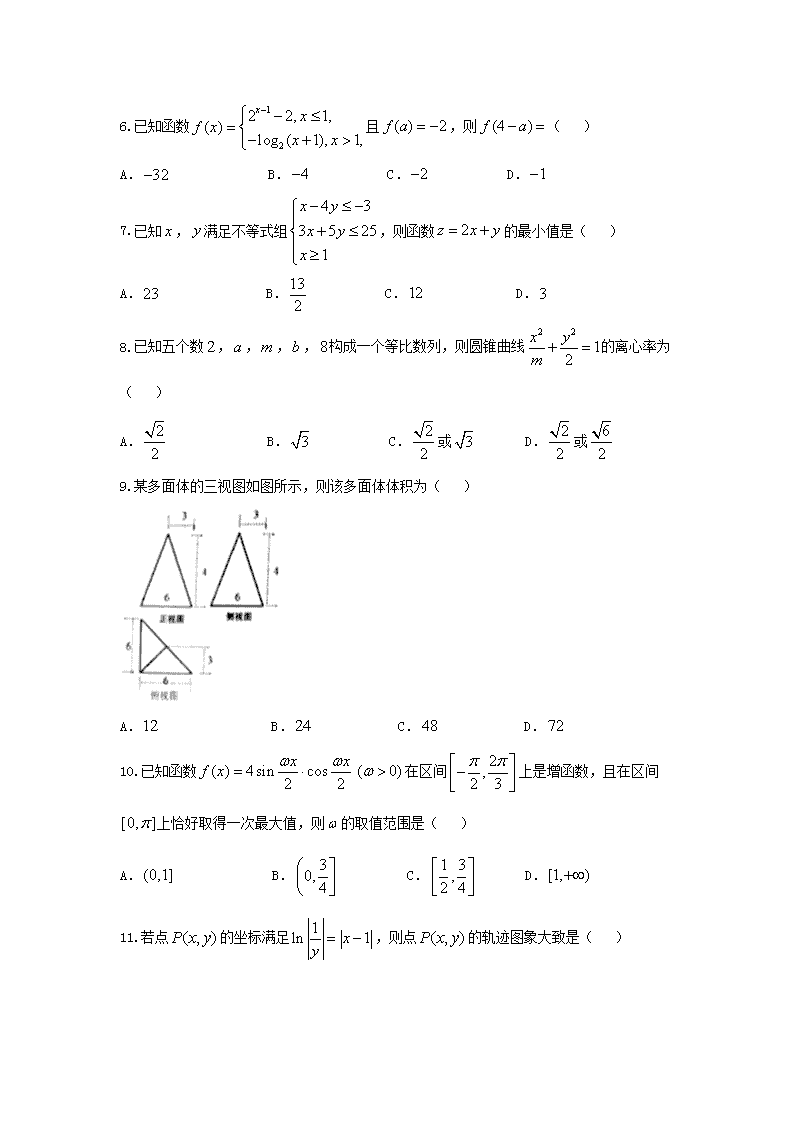- 512.00 KB
- 2021-06-04 发布
江西省五市八校2018届高三第一次联考
数学(文科)试题
第Ⅰ卷
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,,则( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.设,向量,,且,则( )
A. B. C. D.
4.直线与曲线相切于点,则的值为( )
A. B. C. D.
5.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的,分别为,,则输出的( )
A. B. C. D.
6.已知函数且,则( )
A. B. C. D.
7.已知,满足不等式组,则函数的最小值是( )
A. B. C. D.
8.已知五个数,,,,构成一个等比数列,则圆锥曲线的离心率为( )
A. B. C.或 D.或
9.某多面体的三视图如图所示,则该多面体体积为( )
A. B. C. D.
10.已知函数在区间上是增函数,且在区间上恰好取得一次最大值,则的取值范围是( )
A. B. C. D.
11.若点的坐标满足,则点的轨迹图象大致是( )
A. B. C. D.
12.设,分别为双曲线:的左、右焦点,为双曲线的左顶点,以为直径的圆交双曲线一条渐近线于,两点,且满足,则该双曲线的离心率为( )
A. B. C. D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分.)
13.从编号为,,,……,的件产品中,采用系统抽样的方法抽取容量是的样本,若编号为的产品在样本中,则该样本中产品的最大编号为 .
14.已知,则 .
15.已知函数,则 .
16.已知为球的直径,,是球面上两点且,.若球的表面积为,则棱锥的体积为 .
三、解答题.(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知数列是公差为正数的等差数列,其前项和为,且,,成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项和.
18.为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取
名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分;
(2)从甲班名优秀学员中抽取两人,从乙班名分以下的学员中抽取一人,求三人平均分不低于分的概率.
19.如图,直棱柱的棱长都为,点为棱的中点,点在棱上,且.
(1)求证:平面;
(2)求点到平面的距离.
20.已知抛物线:,过点(其中)作互相垂直的两直线,,直线与抛物线相切于点(在第一象限内),直线与抛物线相交于,两点.
(1)当时,求直线的方程;
(2)求证:直线恒过定点.
21.已知函数.
(1)若在,处取得极值.
①求、的值;
②若存在,使得不等式成立,求的最小值;
(2)当时,若在上是单调函数,求的取值范围.
请考生在(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分.
22.选修4-4:坐标系与参数方程
在直角坐标系中,直线的参数方程为(为参数),在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴)中,圆的方程为.
(1)求圆的圆心到直线的距离;
(2)设圆与直线交于点,,若点的坐标为,求.
23.选修4-5:不等式选讲
已知函数.
(1)当时,求函数的定义域;
(2)若关于的不等式的解集是,求实数的取值范围.
江西省五市八校2018届高三第一次模拟联考
数学(文科)试题答案
一、选择题
1-5: CDCAB 6-10: DDABC 11、12:CD
二、填空题
13. 14. 15. 16.
三、解答题
17.(1),
,
,
,
且,
得,
∴.
(2),
,
.
18.(1)甲组的平均分为;乙组的平均分为.
(2)抽取情况为:
,,;,,;,,;,,;,,;,,;,,;,,;,,;,,;,,;,,.
总共有种.
这种平均分不低于分的情况有种.
所以三人平均分不低于分的概率为.
19.(1)面面,,则面,
面,∴,
,,
∴,,
∴,
∴,,∴面.
(2),即,
解,
即点到面距离为.
20.(1)则,
设,则,解,
此时,:.
(2)由,
解得(舍)或,
此时,
则得:,即过定点.
21.(1)①∵,定义域为,∴,
∴.
又∵,且,∴的最小值为.
22.解:(1)∵(为参数),
∴直线的普通方程为.
∵,∴,
由得曲线的直角坐标方程为.
(2)∵,∴,
设直线上的点,对应的参数分别是,(,).
则,,
∵,∴,∴,
将,代入,得.
∴,
又∵,∴.
23.解:(1)不等式
或,
得.
(2)∵,此题可转化为,
由均值不等式,∴得.