中考数学总复习一次函数压轴题专题练习（pdf，含解析） 33页

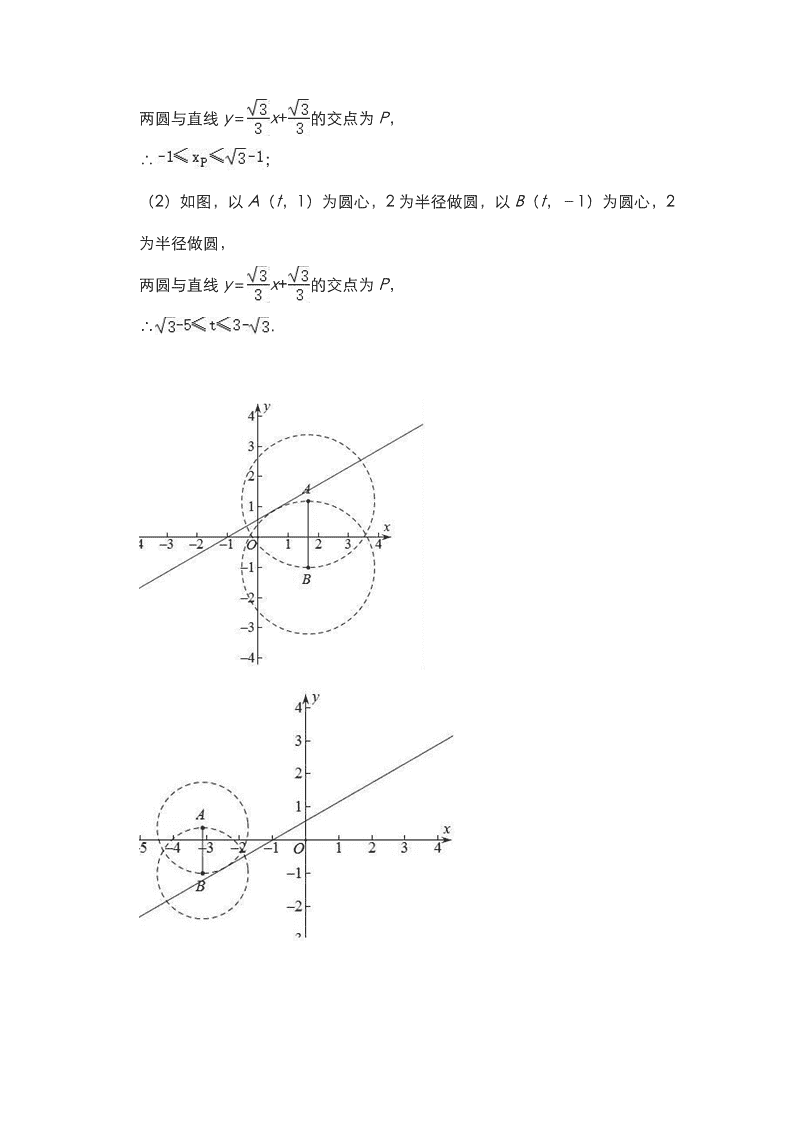
2020 年中考数学总复习一次函数压轴题专题练习 1．如图，在平面内，点 Q 为线段 AB 上任意一点，对于该平面内任意的点 P， 若满足 PQ 小于等于 AB，则称点 P 为线段 AB 的“限距点”． （1）在平面直角坐标系 xOy 中，若点 A（﹣1，0），B（1，0）． ①在的点 C（0，2），D（﹣2，﹣2），E（0，﹣ ）中，是线段 AB 的“限 距点”的是 E ； ②点 P 是直线 y＝ x+ 上一点，若点 P 是线段 AB 的“限距点”，请求出 点 P 横坐标 xP 的取值范围． （2）在平面直角坐标系 xOy 中，若点 A（t，1），B（t，﹣1）．若直线 y＝ x+ 上存在线段 AB 的“限距点”，请直接写出 t 的取值范围 解：（1）①当 C（0，2）时，C 到 AB 的最短距离 2，∵AB＝2， ∴C 不是线段 AB 的“限距点”； 当 D（﹣2，﹣2）时，D 到 AB 的最短距离 2，∵AB＝2， ∴D 不是线段 AB 的“限距点”； 当 E（0，﹣ ）时，E 到 AB 的最短距离 ，∵AB＝2， ∴E 是线段 AB 的“限距点”； 故答案为 E； 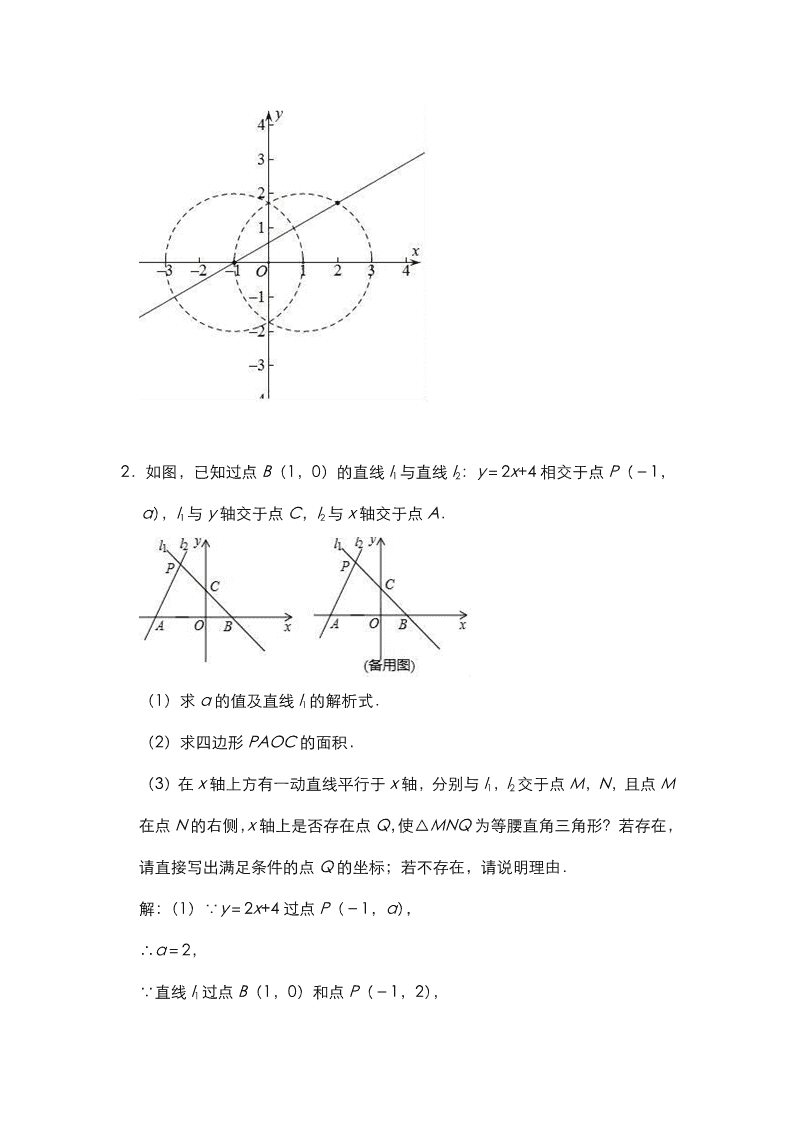②如图：以（1，0）为圆心，2 为半径做圆，以（﹣1，0）为圆心，2 为半径 做圆， 两圆与直线 y＝ x+ 的交点为 P， ∴ ； （2）如图，以 A（t，1）为圆心，2 为半径做圆，以 B（t，﹣1）为圆心，2 为半径做圆， 两圆与直线 y＝ x+ 的交点为 P， ∴ ． 2．如图，已知过点 B（1，0）的直线 l1 与直线 l2：y＝2x+4 相交于点 P（﹣1， a），l1 与 y 轴交于点 C，l2 与 x 轴交于点 A． （1）求 a 的值及直线 l1 的解析式． （2）求四边形 PAOC 的面积． （3）在 x 轴上方有一动直线平行于 x 轴，分别与 l1，l2 交于点 M，N，且点 M 在点 N 的右侧，x 轴上是否存在点 Q，使△MNQ 为等腰直角三角形？若存在， 请直接写出满足条件的点 Q 的坐标；若不存在，请说明理由． 解：（1）∵y＝2x+4 过点 P（﹣1，a）， ∴a＝2， ∵直线 l1 过点 B（1，0）和点 P（﹣1，2）， 设线段 BP 所表示的函数表达式 y＝kx+b 并解得： 函数的表达式 y＝﹣x+1； （2）过点 P 作 PE⊥OA 于点 E，作 PF⊥y 轴交 y 轴于点 F， 则 ； （3）如图，M（1﹣a，a），点 N ， ∵MN＝NQ，则 ， ①当 MN＝NQ 时， ②当 MN＝MQ 时， ③当 MQ＝NQ 时， ， ∴ ，∴ ． 综上，点 Q 的坐标为：（﹣ ，0）或（﹣ ，0）或（﹣ ，0）． 3．在平面直角坐标系中，直线 l1：y＝﹣2x+6 与坐标轴交于 A，B 两点，直线 l2： y＝kx+2（k＞0）与坐标轴交于点 C，D，直线 l1，l2 与相交于点 E． （1）当 k＝2 时，求两条直线与 x 轴围成的△BDE 的面积； （2）点 P（a，b）在直线 l2：y＝kx+2（k＞0）上，且点 P 在第二象限．当 四边形 OBEC 的面积为 时． ①求 k 的值； ②若 m＝a+b，求 m 的取值范围． 解：（1）∵直线 l1：y＝﹣2x+6 与坐标轴交于 A，B 两点， ∴当 y＝0 时，得 x＝3，当 x＝0 时，y＝6； ∴A（0，6）B（3，0）； 当 k＝2 时，直线 l2：y＝2x+2（k≠0）， ∴C（0，2），D（﹣1，0） 解 得 ， ∴E（1，4）， ∴△BDE 的面积＝ ×4×4＝8． （2）①连接 OE．设 E（n，﹣2n+6）， ∵S 四边形 OBEC＝S△EOC+S△EOB， ∴ ×2×n+ ×3×（﹣2n+6）＝ ， 解得 n＝ ， ∴E（ ， ）， 把点 E 的人 y＝kx+2 中， ＝ k+2， 解得 k＝4． ②∵直线 y＝4k+2 交 x 轴于 D， ∴D（﹣ ，0）， ∵P（a，b）在第二象限，在线段 CD 上， ∴﹣ ＜a＜0， ∴b＝4a+2， ∴m＝a+b＝5a+2， ∴﹣ ＜m＜2． 4．如图，在平面直角坐标系中，函数 y＝﹣x+2 的图象与 x 轴，y 轴分别交于点 A，B，与函数 y＝ x+b 的图象交于点 C（﹣2，m）． （1）求 m 和 b 的值； （2）函数 y＝ x+b 的图象与 x 轴交于点 D，点 E 从点 D 出发沿 DA 方向， 以每秒 2 个单位长度匀速运动到点 A（到 A 停止运动）．设点 E 的运动时间为 t 秒． ①当△ACE 的面积为 12 时，求 t 的值； ②在点 E 运动过程中，是否存在 t 的值，使△ACE 为直角三角形？若存在， 直接写出 t 的值；若不存在，请说明理由． 解：（1）∵点 C（﹣2，m）在直线 y＝﹣x+2 上， ∴m＝﹣（﹣2）+2＝2+2＝4， ∴点 C（﹣2，4）， ∵函数 y＝ x+b 的图象过点 C（﹣2，4）， ∴4＝ ×（﹣2）+b，得 b＝ ， 即 m 的值是 4，b 的值是 ； （2）①∵函数 y＝﹣x+2 的图象与 x 轴，y 轴分别交于点 A，B， ∴点 A（2，0），点 B（0，2）， ∵函数 y＝ x+ 的图象与 x 轴交于点 D， ∴点 D 的坐标为（﹣14，0）， ∴AD＝16， 由题意可得，DE＝2t，则 AE＝16﹣2t， 由 ，得 ， 则点 C 的坐标为（﹣2，4）， ∵△ACE 的面积为 12， ∴ ＝12， 解得，t＝5 即当△ACE 的面积为 12 时，t 的值是 5； ②当 t＝4 或 t＝6 时，△ACE 是直角三角形， 理由：当∠ACE＝90°时，AC⊥CE， ∵点 A（2，0），点 B（0，2），点 C（﹣2，4），点 D（﹣14，0）， ∴OA＝OB，AC＝4 ， ∴∠BAO＝45°， ∴∠CAE＝45°， ∴∠CEA＝45°， ∴CA＝CE＝4 ， ∴AE＝8， ∵AE＝16﹣2t， ∴8＝16﹣2t， 解得，t＝4； 当∠CEA＝90°时， ∵AC＝4 ，∠CAE＝45°， ∴AE＝4， ∵AE＝16﹣2t， ∴4＝16﹣2t， 解得，t＝6； 由上可得，当 t＝4 或 t＝6 时，△ACE 是直角三角形． 5．如图 1，已知线段 AB 与点 P，若在线段 AB 上存在点 Q，满足 PQ≤AB，则 称点 P 为线段 AB 的“限距点”． （1）如图 2，在平面直角坐标系 xOy（2）中，若点 A（﹣1，0），B（1，0） ①在 C（0，2）2，D（﹣2，﹣2）， 中，是线段 AB 的“限距点” 的是 C，E ； ②点 P 是直线 y＝x+1 上一点，若点 P 是线段 AB 的“限距点”，请求出点 P 横坐标 xP 的取值范围． （2）在平面直角坐标系 xOy 中，点 A（t，1），B（t，﹣1），直线 y＝ 与 x 轴交于点 M，与 y 轴交于点 N．若线段 MN 上存在线段 AB 的“限距点”， 请求出 t 的取值范围． 解：（1）①∵点 A（﹣1，0），B（1，0）， ∴AB＝2， ∵点 C 到线段 AB 的最短距离是 2≤AB， ∴点 C 是线段 AB 的“限距点”， ∵点 D 到线段 AB 的最短距离＝ ＝ ＞AB， ∴点 D 不是线段 AB 的“限距点”， ∵点 E 到线段 AB 的最短距离是 ≤AB， ∴点 E 是线段 AB 的“限距点”， 故答案为：C，E； ②∵点 A（﹣1，0），B（1，0） ∴点 P 为线段 AB 的“限距点”的范围是平行于 AB 且到 AB 距离为 2 两条线 段 和以点 A，点 B 为圆心，2 为半径的两个半圆围成的封闭式图形，如图所 示： 如图 3，直线 y＝x+1 与该封闭式图形的交点为 M，N， ∴点 M 坐标（1，2） 设点 N（x，x+1） ∴（x+1）2+（x+1﹣0）2＝4 ∴x＝﹣1﹣ ∴ ， ∴点 P 横坐标 xP 的取值范围为： ； （2）∵直线 y＝ 与 x 轴交于点 M，与 y 轴交于点 N． ∴点 N（0，2 ），点 M（﹣6，0） 如图 3，线段 AB 的“限距点”的范围所形成的图形与线段 MN 交于点 M， ∵点 M 是线段 AB 的“限距点”， ∴﹣6﹣t＝2， ∴t＝﹣8， 若线段 AB 的“限距点”的范围所形成的图形与线段 MN 相切于点 F，延长 B'A'交 MN 于 E， ∵sin∠FEA'＝sin∠MNO， ∴ ＝ ∴ ∴t＝ ﹣2， ∴t 的取值范围为﹣8≤t≤ ﹣2． 6．如图（1），在平面直角坐标系中，直线 y＝﹣ x+4 交坐标轴于 A、B 两点， 过点 C（﹣4，0）作 CD 交 AB 于 D，交 y 轴于点 E．且△COE≌△BOA． （1）求 B 点坐标为 （0，4） ；线段 OA 的长为 3 ； （2）确定直线 CD 解析式，求出点 D 坐标； （3）如图 2，点 M 是线段 CE 上一动点（不与点 C、E 重合），ON⊥OM 交 AB 于点 N，连接 MN． ①点 M 移动过程中，线段 OM 与 ON 数量关系是否不变，并证明； ②当△OMN 面积最小时，求点 M 的坐标和△OMN 面积． 解：（1）∵直线 y＝﹣ x+4 交坐标轴于 A、B 两点， ∴当 y＝0 时，x＝3，当 x＝0 时，y＝4， ∴点 A 的坐标为（3，0），点 B 的坐标为（0，4）， ∴OA＝3； 故答案为：（0，4），3； （2）∵过点 C（﹣4，0）作 CD 交 AB 于 D，交 y 轴于点 E．且△COE≌△ BOA， ∴OC＝4，OC＝OB，OE＝OA， ∵点 A（3，0）， ∴OA＝3， ∴OE＝3， ∴点 E 的坐标为（0，3）， 设过点 C（﹣4，0），点 E（0，3）的直线解析式为 y＝kx+b， ，得 ， ∴直线 CE 的解析式为 y＝ x+3， 即直线 CD 的解析式为 y＝ x+3， 由 ，得 ， 即点 D 的坐标为（ ， ）； （3）①线段 OM 与 ON 数量关系是 OM＝ON 保持不变， 证明：∵△COE≌△BOA， ∴OE＝OA，∠OEM＝∠OAN， ∵∠BOA＝90°，ON⊥OM， ∴∠MON＝∠BOA＝90°， ∴∠MOE+∠EON＝∠EON+∠NOA， ∴∠MOE＝∠NOA， 在△MOE 和△NOA 中， ， ∴△MOE≌△NOA（SAS）， ∴OM＝ON， 即线段 OM 与 ON 数量关系是 OM＝ON 保持不变； ②由①知 OM＝ON， ∵OM⊥ON， ∴△OMN 面积是： ＝ ， ∴当 OM 取得最小值时，△OMN 面积取得最小值， ∵OC＝4，OE＝3，∠COE＝90°， ∴CE＝5， ∵当 OM⊥CE 时，OM 取得最小值， ∴ ， ∴ ， 解得，OM＝ ， ∴△OMN 面积取得最小值是： ＝ ， 当△OMN 取得最小值时，设此时点 M 的坐标为（a， a+3）， ∴ ＝ ， 解得，a＝﹣ ， ∴ a+3＝ ， ∴点 M 的坐标为（ ， ）， 由上可得，当△OMN 面积最小时，点 M 的坐标是（ ， ）和△OMN 面积是 7．如图，一次函数 y＝ 的图象分别与 x 轴、y 轴交于点 A、B，以线段 AB 为边在第四象限内作等腰直角△ABC，且∠BAC＝90°． （1）试写出点 A、B 的坐标：A（ 4 ， 0 ），B（ 0 ， ﹣3 ）； （2）求点 C 的坐标； （3）求直线 BC 的函数表达式． 解：（1）当 y＝0 时，0＝ x﹣3， 解得：x＝4， 故 A（4，0）； 当 x＝0 时，y＝﹣3， 故 B（0，﹣3）； 故答案为：（4，0），（0，﹣3）； （2）过点 C 作 CD⊥x 轴，垂足为点 D， ∵∠BAC＝90°， ∴∠OAB+∠DAC＝90°， 又∵∠DCA+∠DAC＝90°， ∴∠ACD＝∠OAB， 在△AOB 和△CDA 中 ∴△AOB≌△CDA（AAS）， ∴AD＝OB＝3，CD＝OA＝4， ∴OD＝7， ∴C（7，﹣4）； （3）设直线 BC 的函数表达式为 y＝kx+b 把 B（0，﹣3），C（7，﹣4）代入上式： 得 ， 解之得： ， ∴直线 BC 的函数表达式为 y＝ ． 8．如图 1 所示，在 A、B 两地之间有汽车站 C 站，客车由 A 地驶往 C 站，货 车由 B 地驶往 A 地．两车同时出发，匀速行驶．图 2 是客车、货车离 C 站的 路程 y1，y2（千米）与行驶时间 x（小时）之间的函数关系图象． （1）填空：A，B 两地相距 600 千米；货车的速度是 40 千米/时； （2）求三小时后，货车离 C 站的路程 y2 与行驶时间 x 之间的函数表达式； （3）试求客车与货两车何时相距 40 千米？ 解：（1）由函数图象可得，A，B 两地相距：480+120＝600（km）， 货车的速度是：120÷3＝40（km/h）． 故答案为：600；40； （2）y＝40（x﹣3）＝40x﹣120（x＞3）； （3）分两种情况： ①相遇前：80x+40x＝600﹣40 解之得 x＝ …（8 分） ②相遇后：80x+40x＝600+40 解之得 x＝ 综上所述：当行驶时间为 小时或 小时，两车相遇 40 千米． 9．如图 1，在平面直角坐标系 xOy 中，点 A（2，0），点 B（﹣4，3）． （1）求直线 AB 的函数表达式； （2）点 P 是线段 AB 上的一点，当 S△AOP：S△AOB＝2：3 时，求点 P 的坐标； （3）如图 2，在（2）的条 件下，将线段 AB 绕点 A 顺时针旋转 120°，点 B 落在点 C 处，连结 CP，求△APC 的面积，并直接写出点 C 的坐标． 解：（1）设直线 AB 的函数表达式为 y＝ kx+b， ∵点 A（2，0），点 B（﹣4，3）， ∴ ， 解得： ， ∴直线 AB 的函数表达式为 y＝﹣ x+1； （2）过 B 作 BE⊥x 轴于 E，过 P 作 PD⊥x 轴于 D， ∴PD∥BE， ∵S△AOP：S△AOB＝2：3， ∴ ＝ ， ∵点 B（﹣4，3）， ∴BE＝3， ∵PD∥BE， ∴△APD∽△ABE， ∴ ＝ ＝ ， ∴PD＝2， 当 y＝2 时，x＝﹣2， ∴P（﹣2，2）； （3）点 A（2，0）、点 B（﹣4，3），点 P（﹣2，2）， 则 AP＝2 ，AB＝CA＝3 ， 过点 P 作 HP⊥AC 交 AC 的延长线于点 H， 则 AH＝ AP＝ ，PH＝APsin60°＝ ， △APC 的面积＝ AC×PH＝ ×3 × ＝ ； 设点 C（x，y）， 则 PC2＝PH2+HC2＝15+（ +3 ）2＝95＝（x+2）2+（y﹣2）2…①， CA2＝45＝（x﹣2）2+y2…②， 联立①②并解得：x＝ ，y＝ ， 故点 C（ ， ）． 10．如图，平面直角坐标系中，直线 AB：y＝kx+3（k≠0）交 x 轴于点 A（4， 0），交 y 轴正半轴于点 B，过点 C（0，2）作 y 轴的垂线 CD 交 AB 于点 E， 点 P 从 E 出发，沿着射线 ED 向右运动，设 PE＝n． （1）求直线 AB 的表达式； （2）当△ABP 为等腰三角形时，求 n 的值； （3）若以点 P 为直角顶点，PB 为直角边在直线 CD 的上方作等腰 Rt△BPM， 试问随着点 P 的运动，点 M 是否也在直线上运动？如果在直线上运动，求出 该直线的解析式；如果不在直线上运动，请说明理由． 解：将点 A 的坐标代入直线 AB：y＝kx+3 并解得：k＝﹣ ， 故 AB 的表达式为：y＝﹣ x+3； （2）当 y＝2 时，x＝ ，故点 E（ ，2），则点 P（n+ ，2）， 而点 A、B 坐标分别为：（4，0）、（0，3）， 则 AP2＝（ +n﹣4）2+4；BP2＝（n+ ）2+1，AB2＝25， 当 AP＝BP 时，（ +n﹣4）2+4＝（n+ ）2+1，解得：n＝ ； 当 AP＝AB 时，同理可得：n＝ + （不合题意值已舍去）； 当 AB＝BP 时，同理可得：n＝﹣ +2 ； 故 n＝ 或 + 或﹣ +2 ； （3）在直线上，理由： 如图，过点 M 作 MD⊥CD 于点 H， ∵∠BPC+∠PBC＝90°，∠BPC+∠MPH＝90°， ∴∠CPB＝∠MPH，BP＝PM，∠MHP＝∠PCB＝90° ∴MHP△≌△PCB（AAS）， 则 CP＝MH＝n+ ，BC＝1＝PH， 故点 M（n+ ，n+ ）， 故点 M 在直线 y＝x+1 上． 11．小聪和小慧去某风景区游览，两人在景点古刹处碰面，相约一起去游览景点 飞瀑，小聪骑自行车先行出发，小慧乘电动车出发，途径草甸游玩后，再乘 电动 车去飞瀑，结果两人同时到达飞瀑．图中线段 OA 和折线 B﹣C﹣D﹣A 表示小聪、小慧离古刹的路程 y（米）与小聪的骑行时间 x（分）的函数关系 的图象，根据图中所给信息，解答下列问题： （1）小聪的速度是多少米/分？从古刹到飞瀑的路程是多少米？ （2）当小慧第一次与小聪相遇时，小慧离草甸还有多少米？ （3）在电动车行驶速度不变的条件下，求小慧在草甸游玩的时间． 解：（1） （米/分）． 古刹到飞瀑的路程＝180×50＝9000（米）． 答：小聪的速度是 180 米/分，从古刹到飞瀑的路程是 9000 米； （2）设 y＝kx+b，则 ， 解得 ， ∴y＝450x﹣4500 当 x＝20，y＝4500450 0﹣3000＝1500 米 答：小慧与小聪第一次相遇时，离草甸还有 1500 米． （3）9000﹣4500＝4500（米） 4500÷450＝10（分钟）． 50﹣10﹣10﹣10＝20（分钟） 答：20 分钟． 12．对于平面直角坐标系 xOy 中，已知点 A（﹣2，0）和点 B（3，0），线段 AB 和线段 AB 外的一点 P，给出如下定义：若 45°≤∠APB≤90°时，则称 点 P 为线段 AB 的可视点，且当 PA＝PB 时，称点 P 为线段 AB 的正可视点． （1）①如图 1，在点 P1（3，6），P2（﹣2，﹣5），P3（2，2）中，线段 AB 的可视点是 P2，P3 ； ②若点 P 在 y 轴正半轴上，写出一个满足条件的点 P 的坐标： P（0，3）（答 案不唯一） ． （2）在直线 y＝x+b 上存在线段 AB 的可视点，求 b 的取值范围； （3）在直线 y＝﹣x+m 上存在线段 AB 的正可视点，直接写出 m 的取值范围． 解：（1）①如图 1，以 AB 为直径作圆 G，则点 P 在圆上，则∠APB＝90°， 若点 P 在圆内，则∠APB＞90°， 以 C（ ， ）为圆心，AC 为半径作圆，在点 P 优弧 上时，∠APB＝45 °，点 P 在优弧 内，圆 G 外时，45°＜∠APB＜90°； 以 D（ ，﹣ ）为圆心，AD 为半径作圆，在点 P 优弧 上时，∠APB＝ 45°，点 P 在优弧 内，圆 G 外时，45°＜∠APB＜90°； ∵点 P1（3，6），P2（﹣2，﹣5），P3（2，2） ∴P1C＝ ＞ ＝AC，则点 P1 在圆 C 外，则∠AP1B＜45°， P2D＝ ＝AC，则点 P2 在圆 D 上，则∠AP2B＝45°， P3G＝ ＝BG，点 P3 在圆 G 上，则∠AP3B＝90°， ∴线段 AB 的可视点是 P2，P3， 故答案为：P2，P3； ②由图 1 可得，点 P 的坐标：P（0，3）（答案不唯一，纵坐标 yp 范围： ≤ yp≤6）． （2）如图 2，设直线 y＝x+b 与圆 C 相切于点 H，交 x 轴于点 N，连接 BH， ∵∠HNB＝∠HBN＝45°， ∴NH＝BH，∠NHB＝90°，且 NH 是切线， ∴BH 是直径， ∴BH＝5 ， ∴BN＝10， ∴ON＝7， ∴点 N（﹣7，0） ∴0＝﹣7+b， ∴b＝7， 当直线 y＝x+b 与圆 D 相切 同理可求：b＝﹣8 ∴﹣8≤b≤7 （3）如图 3，作 AB 的中垂线，交⊙C 于点 Q，交⊙D 于点 W， ∵直线 y＝﹣x+m 上存在线段 AB 的正可视点， ∴线段 CQ 和线段 DW 上的点为线段 AB 的正可视点． ∵点 C（ ， ），点 D（ ，﹣ ），点 Q（ ， + ），点 W（ ，﹣ ﹣ ）分别代入解析式可得： ∴m＝3，m＝ +3，m＝﹣2，m＝﹣2﹣ ， ∴m 的取值范围： 或 ． 13．已知 A、B 两地之间有一条 270 千米的公路，甲、乙两车同时出发，甲车以 每小时 60 千米/时的速度沿此公路从 A 地匀速开往 B 地，乙车从 B 地沿此公 路匀速开往 A 地，两车分别到达目的地后停止甲、乙两车相距的路程 y（千 米）与甲车的行驶时间 x（时）之间 的函数关系如图所示： （1）乙年的速度为 75 千米/时，a＝ 3.6 ，b＝ 4.5 ； （2）求甲、乙两车相遇后 y 与 x 之间的函数关系式，并写出相应的自变量 x 的取值范围． 解：（1）乙车的速度为：（270﹣60×2）÷2＝75 千米/时， a＝270÷75＝3.6，b＝270÷60＝4.5． 故答案为：75；3.6；4.5； （2）60×3.6＝216（千米）， 故 A（2，0），B（3.6，216），C（4.5，270） 当 2＜x≤3.6 时，设 y＝k1x+b1，根据题意得： ， 解得 ， ∴y＝135x﹣270（2＜x≤3.6）； 当 3.6＜x≤4.5 时，设 y＝k2x+b2，则 ， 解得 ， ∴当 3.6＜x≤4.5 时，y＝60x， ∴y＝ ． 14．已知：在平面直角坐标系中，直线 y＝ x+4 与 x 轴交于点 A，与 y 轴交于 点 B，点 C 是 x 轴正半轴上一点，AB＝AC，连接 BC． （1）如图 1，求直线 BC 解析式； （2）如图 2，点 P、Q 分别是线段 AB、BC 上的点，且 AP＝ BQ，连接 PQ．若 点 Q 的横坐标为 t，△BPQ 的面积为 S，求 S 关于 t 的函数关系式，并写出自 变量取值范围； （3）如图 3，在（2）的条件下，点 E 是线段 OA 上一点，连接 BE，将△ABE 沿 BE 翻折，使翻折后的点 A 落在 y 轴上的点 H 处，点 F 在 y 轴上点 H 上方 EH＝FH，连接 EF 并延长交 BC 于点 G，若 BG＝ AP，连接 PE，连接 PG 交 BE 于点 T，求 BT 长． 解：（1）由已知可得 A（﹣3，0），B（0，4）， ∴OA＝3，OB＝4， ∴AB＝ ＝ ＝5， ∵AB＝AC， ∴AC＝5， ∴C（2，0）， 设 BC 的直线解析式为 y＝kx+b， 将点 B 与点 C 代入，得 ， ∴ ， ∴BC 的直线解析式为 y＝﹣2x+4； （2）过点 Q 作 MQ⊥y 轴，与 y 轴交于点 M，过点 Q 作 QE⊥AB，过点 C 作 CF⊥AB， ∵Q 点横坐标是 t， ∴MQ＝t， ∵MQ∥OC， ∴ ， ∴ ， ∴BQ＝ t， ∵AP＝BQ， ∴AP＝ t， ∵AB＝5， ∴PB＝5﹣ t， 在等腰三角形 ABC 中，AC＝AB＝5，BC＝2 ， ∵ AB×CF＝ AC×OB， ∴CF＝OB＝4， ∵EQ∥CF ∴ ∴EQ＝2t， ∴S＝ ×（5﹣ t）＝ （0≤t≤2）； （3）如图 3， ∵将△ABE 沿 BE 翻折，使翻折后的点 A 落在 y 轴上的点 H 处， ∴AH＝AB＝5，AE＝EH， ∴OH＝B H﹣OB＝1， ∵EH2＝EO2+OH2， ∴AE2＝（4﹣AE）2+1， ∴AE＝ ＝EH， ∴OE＝ ， ∴点 E（﹣ ，0） ∵EH＝FH＝ ， ∴OF＝ ∴点 F（0， ） ∴直线 EF 解析式为 y＝ x+ ， 直线 BE 的解析式为：y＝3x+4， ∴﹣2x+4＝ x+ ， ∴x＝ ， ∴点 G（ ， ） ∴BG＝ ＝ ， ∵BG＝ AP， ∴AP＝1， 设点 P（a， a+4） ∴1＝ ∴a＝﹣ ， ∴点 P（﹣ ， ）， ∴直线 PG 的解析式为：y＝ x+ ， ∴3x+4＝ x+ ， ∴x＝﹣1， ∴点 T（﹣1，1） ∴BT＝ ＝ 15．如图，在平面直角坐标系中，点 A（4，0）、点 B（0，4），过原点的直线 l 交直线 AB 于点 P． （1）∠BAO 的度数为 45 °，△AOB 的面积为 8 ； （2）当直线 l 的解析式为 y＝3x 时，求△AOP 的面积； （3）当 时，求直线 l 的解析式． 解：（1）∵点 A（4，0）、点 B（0，4）， ∴OA＝OB， ∵∠AOB＝90°， ∴△AOB 是等腰直角三角形， ∴∠BAO＝45°，△AOB 的面积＝ ×4×4＝8； 故答案为：45，8； （2）设直线 AB 的解析式为：y＝kx+b， 把点 A（4，0）、点 B（0，4）代入得 ， 解得： ， ∴直线 AB 的解析式为：y＝﹣x+4， ∵直线 l 的解析式为 y＝3x， 解 得， ， ∴P（1，3）， ∴△AOP 的面积＝ ×4×3＝6； （3）如图，过 P 作 PC⊥OA 于 C， 则 PC∥OB， ∵ ， ∴ ＝ ， ∴ ＝ ， ∵PC∥OB， ∴△APC∽△ABO， ∴ ＝ ＝ ， ∴ ＝ ＝ ， ∴PC＝1，AC＝1， ∴OC＝3， ∴P（3，1）， ∴ 直线 l 的解析式为 y＝ x．