- 279.00 KB
- 2021-06-04 发布
中原名校联盟2018-2019学年高三第五次质量考评
文数试题
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分.共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.己知集合A={x|x2-2x-15<0},B={x|0<x<7},则A∪B=
A.(-3,7) B.(-3,7] C.(-5,7) D.[-5,-7]
2.复数Z满足(i为虚数单位),则|Z|=
A.1 B. C.2 D.
3.若函数f(x)的定义域是[-1,1],则f(sinx)的定义域是
A.R B.[-1,1] C.[-,] D.[-sin1,sin1]
4.设双曲线C:的右焦点为F1,则F1到渐近线的距离为
A.1 B. C. D.2
5.已知实数x,y满足,则z=x+3y的最大值是
A.4 B.7 C.8 D.
6.已知,,c,则a,b,c的大小关系为
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
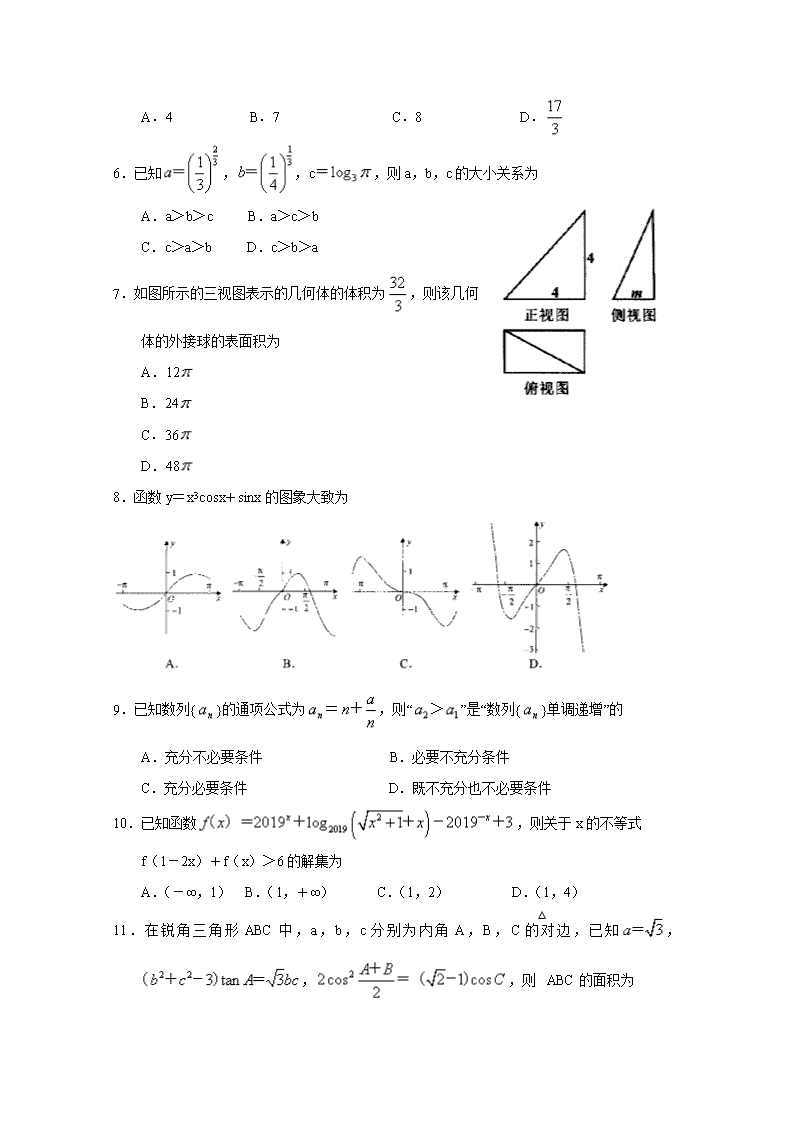
7.如图所示的三视图表示的几何体的体积为,则该几何
体的外接球的表面积为
A.12
B.24
C.36
D.48
8.函数y=x3cosx+sinx的图象大致为
9.已知数列{}的通项公式为=,则“>”是“数列{}单调递增”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10.已知函数,则关于x的不等式
f(1-2x)+f(x)>6的解集为
A.(-∞,1) B.(1,+∞) C.(1,2) D.(1,4)
11.在锐角三角形ABC中,a,b,c分别为内角A,B,C的对边,已知,,,则△ABC的面积为
A. B. C. D.
12.设f(x)是定义在R上的奇函数,且f(4)=0,当x>0时,有<0恒成立,则不等式x2f(x)>0的解集是
A.(-∞,-4)∪(4,+∞) B.(-∞,-4)∪(0,4)
C.(-4,0)∪(4,+∞) D.(-4,0)∪(0,4)
第Ⅱ卷
二、填空题(每小题5分,共20分)
13.已知α∈,tanα=3,则sin2α+2sinαcosα=__________.
14.已知=(0,1),||=2,且|+|=,则与的夹角为_________.
15.已知f(x)是定义在R上周期为4的奇函数,当x∈(0,2)时,f(x)=2x+log2x,则f(2019)= __________.
16.己知,(∈)设,试确定实数m的
取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)] 2-
[log(m-1)m] 2恒成立.则m的取值范围__________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知数列{}的前项和为,且满足,∈.
(1)求数列{}的通项公式;
(2)令,记数列的前项和为,证明:.
18.(本小题满分12分)
科学技术是第一生产力,某学校大力推行“信息云课堂”改革,为了让广大教师认识到改革的必要性和有效性,从而积极主动投身到“信息云课堂”改革当中,特将刚入学的高一年级全体学生按照学生入学成绩和人数平均分成A组和B组作为实验比较对象,其中A组的班级采用“信息课堂模式”,B组班级沿用过去传统的教学模式,实验周期为一学期。学期结束,从每组中随机抽取50名学生独立参加测试,测试成绩(百分制)统计如下表:
(1)根据上表,分别估算A组和B组被抽取学生的平均成绩以及中位数;
(2)完成下面2×2联表,并回答有多大的把握认为“信息云课堂改革是必须和有效的”?
19.(本小题满分12分)
在平行四边形EAFC的边AF和CE上分别选取B点D点使得ABCD是正方形,并将面EAD和面CBF分别沿AD,BC折叠起来使得在多面体ABCDEF中,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,取棱AE的中点记为点M.
(1)求证:平面BMD∥平面EFC;
(2)若AB=l,BF=2,求三棱锥A-CEF的体积.
20.(本小题满分12分)
动点P到定点F(0,1)的距离比它到X轴的距离大l,设动点P的轨迹为曲线C,过点F的直线交曲线C于A,B两个不同的点,过点A,B分别作曲线C的切线,且二者相交于点M.
(1)求曲线C的方程;
(2)求证:=0;
(3)求△ABM的面积的最小值.
21.(本小题满分12分)
己知函数f(x)=x2-x+alnx(a>0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2,求证:>·
请考生在第22、23两题中任选一题做答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.【选修4-4:坐标系与参数方程】(10分)
若直线l的极坐标方程为ρcosθ+2ρsinθ-m=0,曲线C的参数方程为(为参数).
(1)若曲线上存在M,N两点关于直线l对称,求实数m的值;
(2)若直线与曲线相交于P,Q两点,且|PQ|≤4,求实数m的取值范围.
23.【选修4-5:不等式选讲】(10分)
设函数f(x)=|x-2|-|2x+1|.
(1)解不等式f(x)≤0;
(2)x0∈R,使得f(x0)-2m2≥4m成立,求实数m的取值范围.