四川省广安市岳池一中2020届高三上学期期中考试数学试卷 含答案 5页

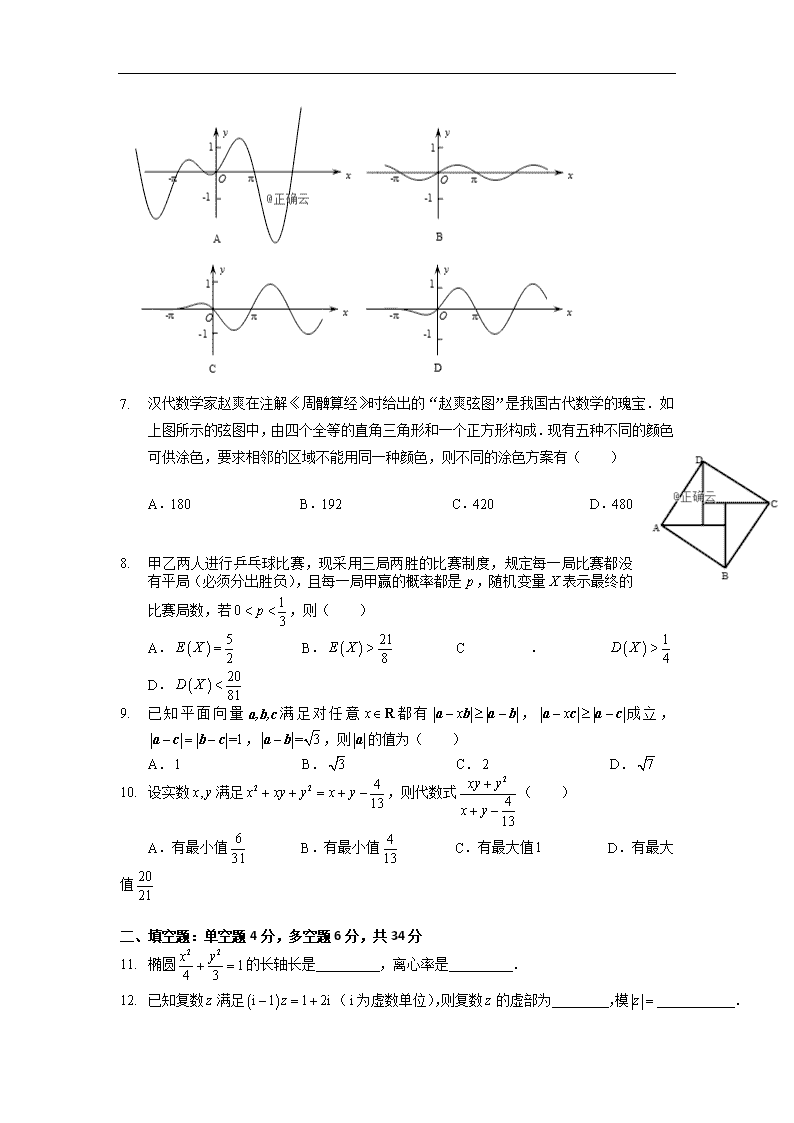
‎ 数学试卷 一、选择题：每小题4分，共40分 ‎ 1. 已知集合，，则（ ）‎ A． B． C． D．‎ 2. 以下哪个点在倾斜角为且过点的直线上（ ）‎ A． B． C． D．‎ 3. 某几何体的三视图如图所示，则该几何体的体积是（ ）‎ A． B． C． D．‎ 4. 若实数满足，则的最大值是（ ）‎ A． B． C． D．‎ 5. 已知平面，直线满足，，则“”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎ 6. 设函数，则的图像大致为（ ）‎ 1. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝．如上图所示的弦图中，由四个全等的直角三角形和一个正方形构成．现有五种不同的颜色可供涂色，要求相邻的区域不能用同一种颜色，则不同的涂色方案有（ ）‎ A．180 B．192 C．420 D．480 ‎ 2. 甲乙两人进行乒乓球比赛，现采用三局两胜的比赛制度，规定每一局比赛都没有平局（必须分出胜负），且每一局甲赢的概率都是，随机变量表示最终的比赛局数，若，则（ ）‎ A． B． C． D．‎ 3. 已知平面向量满足对任意都有，成立，，，则的值为（ ）‎ A． B． C． D．‎ 4. 设实数满足，则代数式（ ）‎ A．有最小值 B．有最小值 C．有最大值 D．有最大值 二、填空题：单空题4分，多空题6分，共34分 5. 椭圆的长轴长是 ，离心率是 ．‎ 6. 已知复数满足（为虚数单位），则复数的虚部为 ，模 ．‎ 1. 二项式展开的所有项的系数和为 ，展开式中的常数项是 ．‎ 2. 已知二次函数，一次函数，不等式的解集为，则 ；记函数，则的最小值是 ．‎ 3. 若，，则 ．‎ 4. 已知为双曲线：上的一点，，分别为的左右焦点，若的内切圆的直径为，则双曲线的离心率的取值范围为 ．‎ 5. 已知数列满足，，，记数列的前项和为，则对任意，有①数列单调递增；②；③；④．上述四个结论中正确的是 ．（填写相应的序号）‎ 三、解答题：4小题，共56分 6. 已知．‎ ‎（1）求的最小正周期及最大值；‎ ‎（2）在三角形中，内角，，所对的边分别是，，，且，，，求的面积． ‎ 7. 如图所示，四棱锥中，底面是平行四边形，平面，，，是中点，点在棱上移动．‎ ‎（1）若，求证：；‎ ‎（2）若，当点为中点时，求与平面所成角的大小． ‎ 1. 设各项均为正数的数列的前项和为，满足，已知等比数列，，，．‎ ‎（1）求数列，的通项公式；‎ ‎（2）记，数列的前项和为，证明：对一切正整数，． ‎ 2. 已知抛物线的图像经过点．‎ ‎（1）求抛物线的方程和焦点坐标；‎ ‎（2）直线交抛物线于不同的两点，且位于轴两侧，过分别作抛物线的两条切线 交于点，直线与轴的交点分别记作．记的面积为，的面积为，‎ 的面积为，试问是否为定值，若是，请求出该定值；若不是，请说明理由．‎ 1. 已知函数，‎ ‎（1）若，求出函数的单调区间及最大值；‎ ‎（2）若且，求函数在上的最大值的表达式．‎