- 1.56 MB
- 2021-06-04 发布
福州文博中学2016-2017学年
高二年级下学期期中考试数学科(理)题目卷
命题人:池哲进 审核人:余光亮
(完卷时间:120分钟,总分:150分)
一、 选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的序号填在答题纸上.)
1、复数(为虚数单位)的共轭复数为( )
A. B. C. D.
2、根据定积分的定义知=( )
A. B. C. D、
3、设命题甲:的解集是实数集;命题乙:,则命题甲是命题乙成立的( )
A.充分不必要条件 B.充要条件 C.必要不充分条件 D.既不充分也不必要条件
4、下列等于1的积分是( )
A. B. C. D、
5、函数的单调递减区间是( )
A. B. C. D.
6、设曲线在点处的切线与直线垂直,则等于 ( )
A.2 B.-2 C. D.-
7、等差数列中,是一个与无关的常数,则该常数的可能值的集合为( )
A. B. C. D.
8、在棱长为的正方体中,则平面与平面间的距离 ( )
A. B. C . D.
9、用数学归纳法证明,从到,左边需要增乘的代数式为( )
A. B. C. D.
10、在中,角所对边分别为, 且,, ,则的面积为( )
A. B. C. D.
11、设点P是双曲线(a>0,b>0)与圆=在第一象限的交点, F1,F2分别是双曲线的左、右焦点,且|PF1|=3|PF2|,则双曲线的离心率为( )
A. B. C. D.
12、定义表示实数中的较大的数.已知数列满足 ,若,记数列的前项和为,则的值为( )
A.7254 B.7255 C.7256 D.7257
二、填空题:(本大题共4小题,每小题5分,共20分。在答题卡作答).
13、 .
14、某圆锥曲线是椭圆或双曲线,若其中心为坐标原点,对称轴为坐标轴,且过点,,则圆锥曲线是 .
15、已知ABCD为平行四边形,且A(4,1,3)、B(2,-5,1),C(3,7,-5),则顶点D的坐标为________.
16、已知函数=,其导函数记为,则= .
三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.)
17、(本小题满分10分)在△ABC中,a、b、c分别是角A,B,C的对边,且=-.
(1)求角B的大小; (2)若b=,a+c=4,求△ABC的面积.
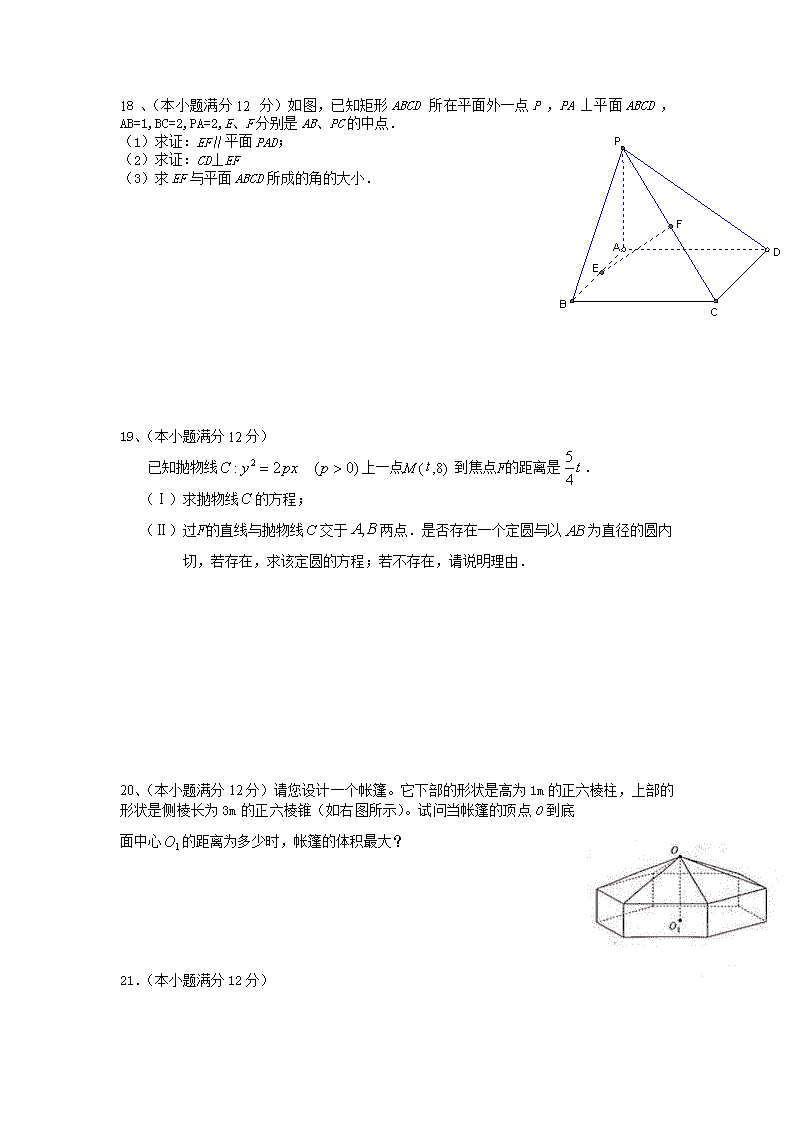
18、(本小题满分12分)如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求证:CD⊥EF
(3)求EF与平面ABCD所成的角的大小.
19、(本小题满分12分)
已知抛物线上一点M (,8) 到焦点F的距离是.
(Ⅰ)求抛物线的方程;
(Ⅱ)过F的直线与抛物线交于两点.是否存在一个定圆与以为直径的圆内切,若存在,求该定圆的方程;若不存在,请说明理由.
20、(本小题满分12分)请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心的距离为多少时,帐篷的体积最大?
21.(本小题满分12分)
如图,直三棱柱中,,,D是AB中点.
(Ⅰ)记平面平面,在图中作出,并说明画法;
(Ⅱ)求直线与平面所成角的正弦值.
22、(本小题满分12分)已知函数,.
(Ⅰ)若曲线在点处的切线斜率为1,求实数的值;
(Ⅱ)当时,证明:.
福州文博中学2016-2017学年
高二年级下学期期中考试理科数学(答题卷)
(完卷时间:120分钟,总分:150分)
题号
一
二
三
总分
17
18
19
20
21
22
得分
评卷教师
一、选择题:(本大题共12小题,每小题 5分,共 60分)
1
2
3
4
5
6
7
8
9
10
11
12
A
D
C
C
B
B
D
B
A
D
D
A
二、填空题:(本题共4小题,每小题5 分,共20分)
13、 14、 双曲线
15、 16、 2
三、解答题:(本大题共6小题,共70分)
17. (本小题满分10分)
1)由余弦定理知:cosB=,cosC=.
将上式代入=-得:·=-
整理得:a2+c2-b2=-ac∴cosB== =-
∵B为三角形的内角,∴B=.………………6分
(2)将b=,a+c=4,B=代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB
∴b2=16-2ac,∴ac=3.∴S△ABC=acsinB=.………………12分
18.(本小题满分12分)
19.(本小题满分12分)
18、略
19、考查抛物线的定义与焦半径的知识,焦点弦的性质,利用待定系数方法探究存在性问题,可以较好的考察学生的数学思维能力,数形结合能力及逻辑运算能力。
解法一:
(Ⅰ)由抛物线定义得 又 …………………… 2分
, 在抛物线上,, …………………………3分
解得(舍去)或, 所以抛物线的方程为. …………………………4分
(Ⅱ)当直线的斜率存在,设直线的方程为,
与抛物线交于点,
联立化简得 ,……………………………………5分
显然,…………………………………………………………………6分
设的中点为,则, ………………7分
,……………………………………………………………………8分
设圆的方程为,
,………………………………………………9分
,
…………………………………………………10分
定圆的方程为,……………………………………………………………11分
当直线的斜率不存在,以为直径的圆的方程为,
该圆也与定圆内切.
综上所求定圆的方程为. …………………………………………………12分
解法二:
(Ⅰ)同解法一;
(Ⅱ)设直线的方程为 ,与抛物线交于点.
,化简得,……………………………………………6分
显然, ……………………………………………………………7分
设的中点为,则 , ……8分
,…………………………………………………………9分
由抛物线的对称性可知,若定圆存在其圆心必在轴上,
设圆的方程为,
,…………………………………………10分
,
……………………………………………… 11分
所以定圆的方程为.……………………………………………………12分
解法三:
(Ⅰ)同解法一;
(Ⅱ)当直线的斜率存在,设直线的方程为,与抛物线交于点,
化简得,………………………………5分
显然,………………………………………………………6分
设的中点为,则,…… 7分
,由抛物线的对称性可知,若定圆存在其圆心必在轴上,
设圆的方程为,,……9分
,
………………………………………………10分
定圆的方程为 , …………………………………………………11分
当直线的斜率不存在,以为直径的圆的方程为,
该圆也与定圆内切,
综上所求定圆的方程为. ………………………………………12分
20、分析:本题应该先建立模型,再求体积的最大值。选择适当的变量很关键,设的长度会比较简便。
解:设,则由题设可得正六棱锥底面边长为(单位:m)。
于是底面正六边形的面积为(单位:m2):
。
帐篷的体积为(单位:m3):
求导数,得;
令解得x=-2(不合题意,舍去),x=2。
当1