2020高中数学 第一章 集合与函数概念 1 5页

‎1.2.2‎函数的表示方法（3）‎ ‎【导学目标】 ‎ ‎1.会根据不同的需要选择适当的方法（如图象法、列表法、解析法）表示函数； ‎ ‎2.了解映射的概念．能判断某些对应关系是否是从集合到集合的映射，并会表示一些简单的映射.‎ ‎【自主学习】‎ ‎ 知识回顾：‎ 新知梳理：‎ ‎1.映射的概念 设是两个非空的集合，如果按照某种确定的对应关系，使得对于集合中的______一个元素，集合中都有______确定的元素与之对应，那么就称对应_____________为从______到______的一个映射．‎ ‎【感悟】‎ ‎（1）理解映射的定义要把握好几个词：“任意”、“有”、“唯一”；‎ ‎（2）映射是有方向的，到的映射与到到映射往往不同.‎ 对点练习：1．设，，从到的对应法则，下列对应不是映射的是（ ）．‎ ‎ (A) ： ‎ ‎(B) ：‎ ‎(C) ： ‎ ‎ (D) ：‎ ‎2.映射与函数 列表对比映射与函数：‎ 映射 函数 符号表示 集合要求 为_____集合．‎ 为_____集合．‎ 为_____集合．‎ 为_____集合．‎ 元素对应 要求 中的______一个元素，集合中都有______确定的元素与之对应．‎ 中的_________一个数，集合中都有_________确定的数与之对应．‎ ‎【感悟】从映射的角度去理解函数，就是函数的定义域，函数的值域.‎ 对点练习：2. 下列四种说法正确的是（ ）．‎ ‎(A)表示的是含有的代数式 ‎ ‎(B）函数的值域也就是定义中的数集 ‎(C)函数是一种特殊的映射 ‎ 5‎ ‎（D）映射是一种特殊的函数 ‎【合作探究】‎ 典例精析 例题1：（课本P22例7）以下给出的对应是不是从A到集合B的映射？‎ ‎（1）集合A={P | P是数轴上的点}，集合B=R，对应关系f：数轴上的点与它所代表的实数对应；‎ ‎（2）集合A={P | P是平面直角坐标系中的点}，B= ，对应关系f： 平面直角坐标系中的点与它的坐标对应；‎ ‎（3）集合A={x | x是三角形}，集合B={x | x是圆}，对应关系f：每一个三角形都对应它的内切圆；‎ ‎（4）集合A={x | x是新华中学的班级}，集合B={x | x是新华中学的学生}，对应关系：每一个班级都对应班里的学生。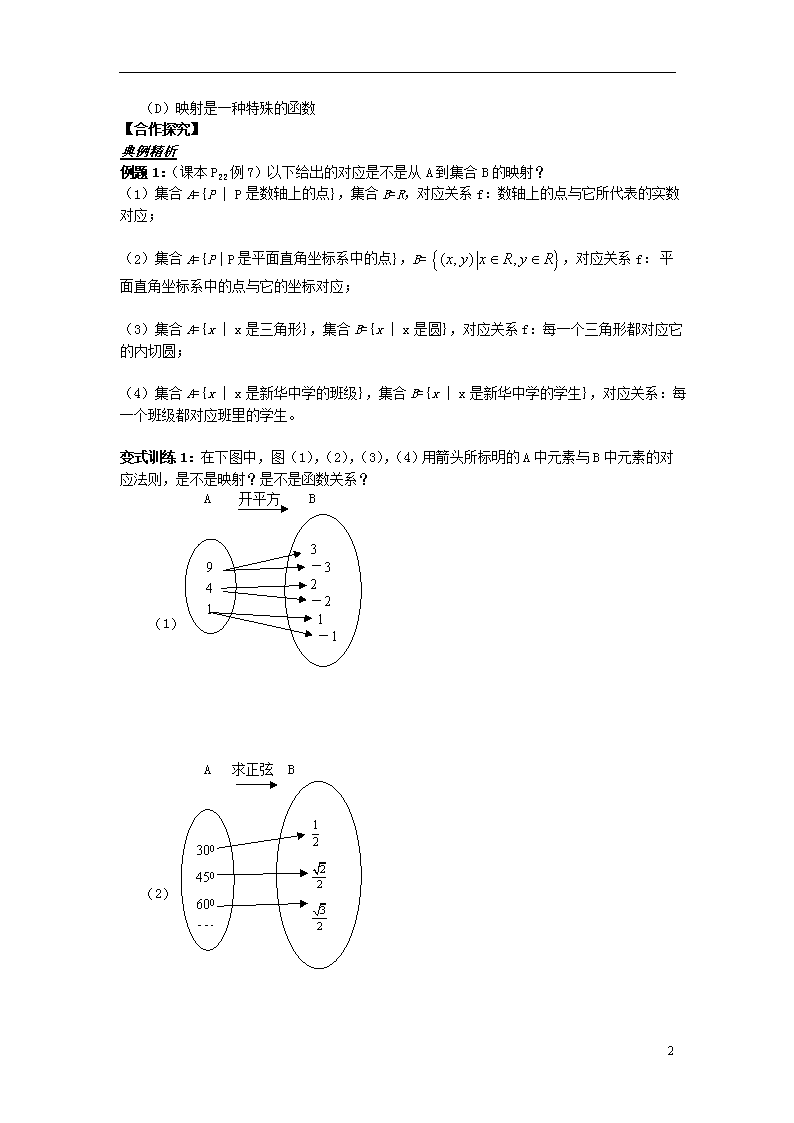‎ 变式训练1：在下图中，图（1），（2），（3），（4）用箭头所标明的A中元素与B中元素的对应法则，是不是映射？是不是函数关系？‎ A 开平方 B ‎ ‎9‎ ‎4‎ ‎1‎ ‎3‎ ‎－3‎ ‎2‎ ‎－2‎ ‎1‎ ‎－1‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎ ‎ ‎（1）‎ ‎ ‎ ‎ A 求正弦 B ‎300‎ ‎450‎ ‎600‎ ‎900‎ ‎1‎ ‎ ‎ ‎（2）‎ 5‎ A 求平方 B ‎ ‎1‎ ‎－1‎ ‎2‎ ‎－2‎ ‎3‎ ‎－3‎ ‎1‎ ‎4‎ ‎9‎ ‎ ‎ ‎（3）‎ ‎ A 乘以2 B ‎（4）‎ 例题2：已知，，用图示法表示所有的集合到集合的映射． ‎ 5‎ 变式训练2：设集合，，试问：从到的映射一共有几个？并将它们分别表示出来。‎ 例题3：集合A中有m个元素，集合B中 有n个元素。则从集合A到集合B可以建立个不同的映射。‎ 5‎ ‎【课堂小结】‎ 5‎