江苏省无锡市2013届高三上学期期中考试数学试题 12页

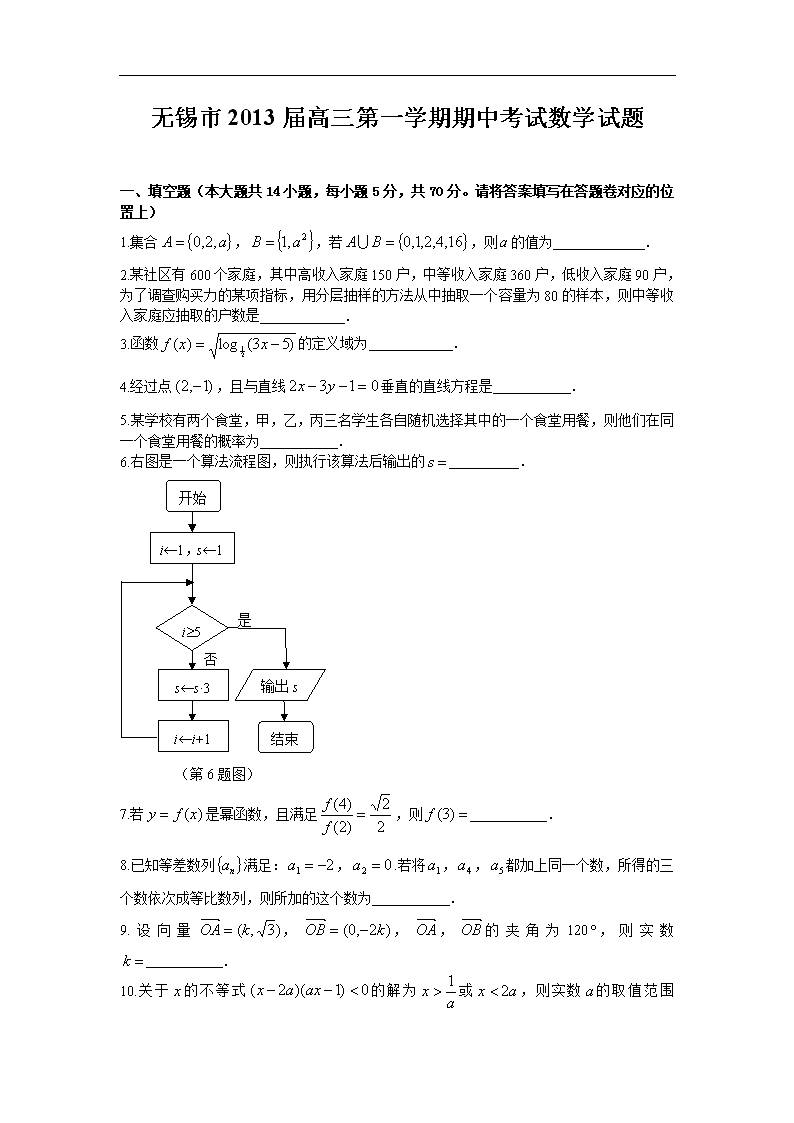
无锡市2013届高三第一学期期中考试数学试题 一、填空题（本大题共14小题，每小题5分，共70分。请将答案填写在答题卷对应的位置上）‎ ‎1.集合，，若，则的值为 ．‎ ‎2.某社区有600个家庭，其中高收入家庭150户，中等收入家庭360户，低收入家庭90户，为了调查购买力的某项指标，用分层抽样的方法从中抽取一个容量为80的样本，则中等收入家庭应抽取的户数是 ．‎ ‎3.函数的定义域为 ．‎ ‎4.经过点，且与直线垂直的直线方程是 ．‎ ‎5.某学校有两个食堂，甲，乙，丙三名学生各自随机选择其中的一个食堂用餐，则他们在同一个食堂用餐的概率为 ．‎ ‎6.右图是一个算法流程图，则执行该算法后输出的 ．‎ 开始 i¬1，s¬1‎ i³5‎ s¬s×3‎ i¬i+1‎ 输出s 结束 否 是 ‎ （第6题图）‎ ‎7.若是幂函数，且满足，则 ．‎ ‎8.已知等差数列满足：，.若将，，都加上同一个数，所得的三个数依次成等比数列，则所加的这个数为 ．‎ ‎9.设向量，，，的夹角为，则实数 ．‎ ‎10.关于的不等式的解为或，则实数 的取值范围为 ．‎ ‎11.以下5个命题：‎ ‎（1）设，，是空间的三条直线，若，，则；‎ ‎（2）设，是两条直线，是平面，若，，则；‎ ‎（3）设是直线，，是两个平面，若，，则；‎ ‎（4）设，是两个平面，是直线，若，，则；‎ ‎（5）设，，是三个平面，若，，则.‎ 其中正确命题的序号是 ．‎ 12. 函数为奇函数，则的减区间为 ．‎ 13. 已知，，若对任意，总存在，使得成立，则实数的取值范围是 ．‎ ‎14.定义在R上的函数是增函数，且函数的图象关于成中心对称，设，满足不等式，若时，则的范围是 ．‎ 二、解答题：（本大题共6道题，计90分。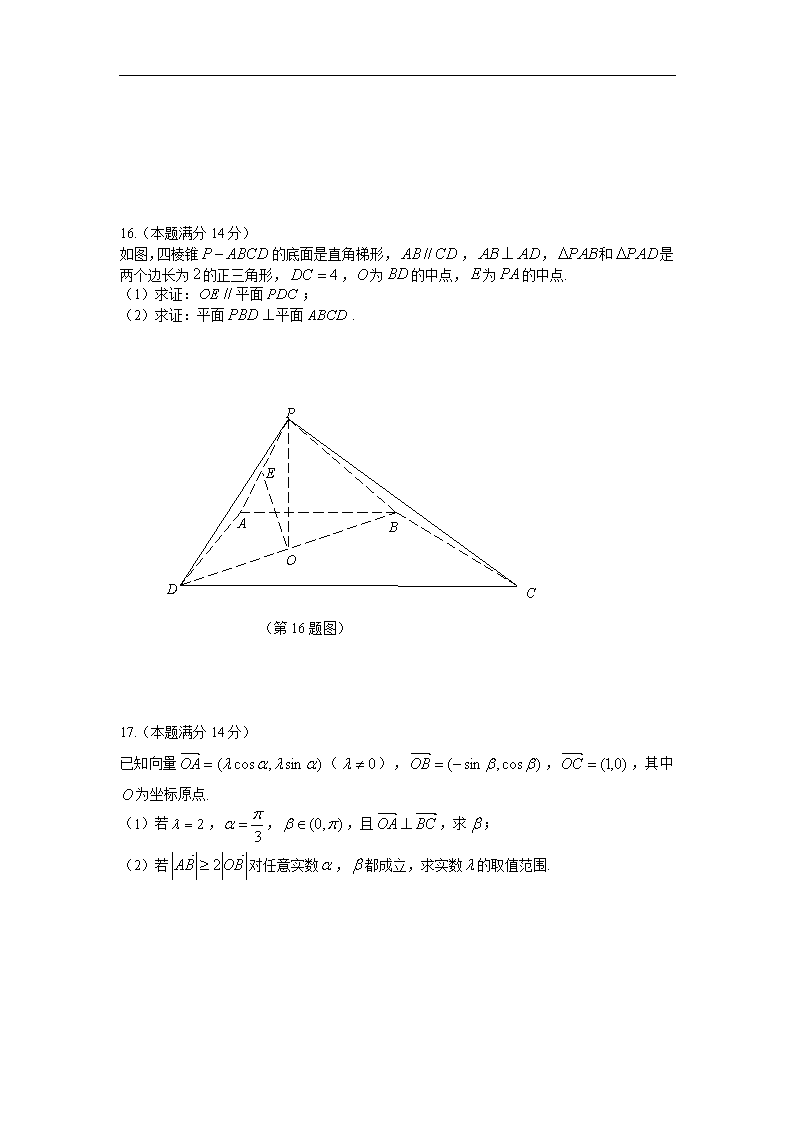解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎15.（本题满分14分）‎ 已知中，角，，的对边分别为，，，且，.‎ （1） 若，求；‎ （2） 若，求的面积.‎ ‎16.（本题满分14分）‎ 如图，四棱锥的底面是直角梯形，，，和是两个边长为的正三角形，，为的中点，为的中点.‎ （1） 求证：平面；‎ （2） 求证：平面平面.‎ D P C B A O E ‎ ‎ ‎（第16题图）‎ ‎17.（本题满分14分）‎ 已知向量（），，，其中为坐标原点.‎ （1） 若，，，且，求；‎ （2） 若对任意实数，都成立，求实数的取值范围.‎ ‎18.（本题满分16分）‎ 数列是公比大于的等比数列，，.‎ （1） 求数列的通项公式；‎ （2） 在与之间插入个数，使这个数组成公差为的等差数列.设第个等差数列的前项和是.求关于的多项式，使得对任意恒成立；‎ （3） 对于（2）中的数列，，，，，，这个数列中是否存在不同的三项，，（其中正整数，，成等差数列）成等比数列？若存在，求出这样的三项；若不存在，说明理由.‎ ‎19.（本题满分16分）‎ 为了保护环境，某化工厂在政府部门的支持下，进行技术改造：每天把工业废气转化为某种化工产品和符合排放要求的气体，经测算，该工厂每天处理废气的成本（元）与处理废气量（吨）之间的函数关系可近似地表示为：，且每处理1吨工业废气可得价值为50元的某种化工产品.‎ （1） 当工厂日处理废气量时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，为了保证工厂在生产中没有亏损现象出现，国家至少每天财政补贴多少元？‎ （2） 若国家给予企业处理废气阶梯式财政补贴，当日废气处理量不足40吨时，给予每顿80元补贴，废气处理量不少于40吨时，超过40吨的部分再增加每顿55元的补贴，当工厂的日处理量为多少吨时，工厂处理每顿废气的平均收益最大？‎ 20. ‎（本题满分16分）‎ 已知函数，（）.‎ （1） 当时，若直线与函数的图象相切，求的值；‎ （2） 若在上是单调减函数，求的最小值；‎ （3） 当时，恒成立，求实数的取值范围.（为自然对数的底）.‎