- 2.76 MB
- 2021-06-04 发布
本专题特别注意:
1.数形结合求定积分
2.分段求定积分
3.定积分的几何意义
4.含绝对值的定积分求法
5.定积分与二项式定理的联系
6.定积分与导数的联系
7.分段函数定积分的求法
8.定积分与概率的联系
方法总结:
1.定积分计算的关键是通过逆向思维获知被积函数的原函数,即导数运算的逆运算.
2.定积分在物理学中的应用必须遵循相应的物理过程和物理原理.
3.利用定积分求平面图形面积的步骤:
(1)画出草图,在直角坐标系中画出曲线或直线的大致图象;
(2)借助图形确定出被积函数,求出交点坐标,确定积分的上、下限;
(3)将曲边梯形面积表示成若干个定积分的和;
(4)计算定积分,写出答案.
高考模拟:
一、单选题
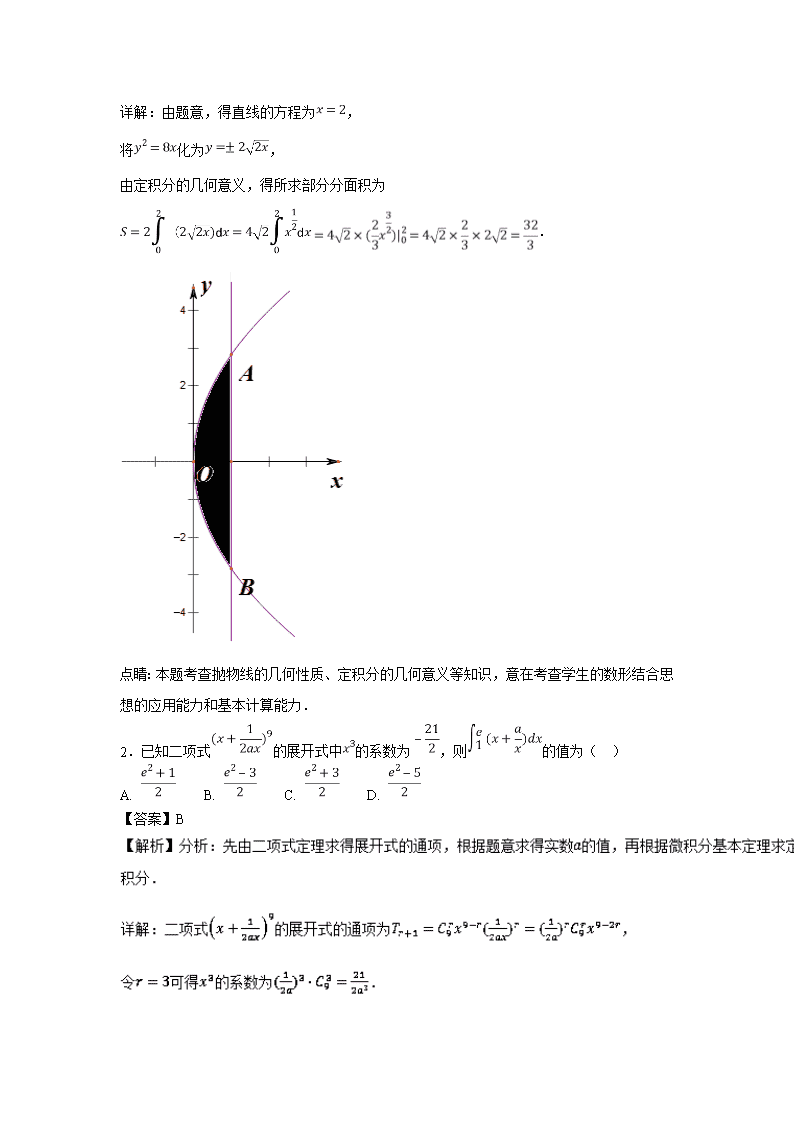
1.直线过抛物线:的焦点且与轴垂直,则直线与所围成的面积等于( )
A. B. C. D.
【答案】C
【解析】分析:先作出直线和抛物线围成的平面区域,再利用定积分的几何意义进行求解.
详解:由题意,得直线的方程为,
将化为,
由定积分的几何意义,得所求部分分面积为
.
点睛:本题考查抛物线的几何性质、定积分的几何意义等知识,意在考查学生的数形结合思想的应用能力和基本计算能力.
2.已知二项式的展开式中的系数为,则的值为( )
A. B. C. D.
【答案】B
由题意得,解得.
所以.
故选B.
点睛:解答本题时注意两点:①正确写出二项展开式的通项,然后解方程得到的值;②求定积分时要正确得到被积函数的原函数,并准确求出函数值.
3.设,则的展开式中常数项是( )
A. B. C. D.
【答案】B
【解析】分析:先根据定积分求得,求出二项展开式的通项后再求展开式中的常数项.
点睛:本题考查用微积分基本定理求定积分和二项展开式的通项的应用,解答的关键式准确写出二项展开式的通项,并根据常数项的特征求解.
4.若函数的图象如图所示,则图中的阴影部分的面积为( )
A. B. C. D.
【答案】C
【解析】分析:由图象求出函数解析式,然后利用定积分求得图中阴影部分的面积.
详解:由图可知,,,即.
∴,则.
∴图中的阴影部分面积为
故选C.
点睛:本题考查了导数在求解面积中的应用,关键是利用图形求解的函数解析式,在运用积分求解.定积分的计算一般有三个方法:①利用微积分基本定理求原函数;②利用定积分的几何意义,利用面积求定积分;③利用奇偶性对称求定积分,奇函数在对称区间的定积分值为0.
5.设,在区间上随机产生10000个随机数,构成5000 个数对,记满足的数对的个数为,则估计值约为( )
A. 3333 B. 3000 C. 2000 D. 1667
【答案】A
【解析】分析:设事件为“上随机产生数对,满足 ”,则总的基本事件为,对应的测度为正方形的面积1,而随机事件对应的测度为为曲边梯形的面积,它可利用定积分来计算.
详解:满足是在曲线、所围成的区域内(含边界),
又该区域的面积为,
故的估计值为,,故选A.
点睛:对于曲边梯形的面积,我们可以用定积分来计算.
6.已知,则( )
A. B. C. D.
【答案】B
7.已知,在的展开式中,记的系数为,则 ( )
A. B. C. D.
【答案】A
【解析】,所以,由已知有指的系数,指的系数,所以,选A.
8.已知,是以a为周期的奇函数,且定义域为,则的值为( )
A. 0 B. 1 C. 2 D. 2018
【答案】A
【解析】
可知的周期为
,
故选
9.用S表示图中阴影部分的面积,则S的值是
A. B.
C. D.
【答案】D
10.已知曲线和直线所围成图形的面积是,则的展开式中项的系数为( )
A. 480 B. 160 C. 1280 D. 640
【答案】D
【解析】
由题意得到两曲线围成的面积为
=
故答案为:D.
点睛:这个题目考查的是二项式中的特定项的系数问题,在做二项式的问题时,看清楚题目是求二项式系数还是系数,还要注意在求系数和时,是不是缺少首项;解决这类问题常用的方法有赋值法,求导后赋值,积分后赋值等.
11.
A. B. C. D.
【答案】A
【解析】.
故选A.
12.已知函数在上可导,且,则( )
A. 1 B. C. D.
【答案】C
13.已知物体运动的速度与事件的关系式为,则落体从到所走的路程为( )
A. B. C. D.
【答案】B
【解析】由积分的物理意义可知运动从t=0到t=5所走的路程为,
故选:B.
14.定积分的值为( )
A. B. C. D.
【答案】A
【解析】表示以为圆心,以为半径的圆, 定积分等于该圆的面积的四分之一, 定积分,故选A.
15.设函数f(x)= 则定积分f(x)dx等于( )
A. B. 2 C. D.
【答案】C
【解析】,故选C.
16.如图所示,在边长为1的正方形中任取一点,则点恰好取自阴影部的概率( )
A. B. C. D.
【答案】C
点睛:(1)当试验的结果构成的区域为长度、面积、体积等时,应考虑使用几何概型求解.
(2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域.
(3)几何概型有两个特点:一是无限性,二是等可能性.基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的区域都是有限的,因此可用“比例解法”求解几何概型的概率.
17.若的展开式中含有常数项,且的最小值为,则
A. B. C. D.
【答案】C
【解析】展开式的通项为
,因为展开式中含有常数项,所以,即为整数,故n的最小值为5.
所以.故选C
点睛:求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第项,再由特定项的特点求出值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第项,由特定项得出值,最后求出其参数.
18.若,则( )
A. B. C. D.
【答案】B
考点:定积分.
19.已知,则展开式中的系数为( )
A. 24 B. 32 C. 44 D. 56
【答案】A
【解析】,中系数为.故选.
20.如图所示,若程序框图输出的所有实数对所对应的点都在函数的图象上,则( )
A. B. C. D.
【答案】B
21.如图,在由, , ,及围成区域内任取一点,则该点落在, 及围成的区域内(阴影部分)的概率为( )
A. B. C. D.
【答案】D
故选:D.
22.已知函数,则( )
A. B. C. D.
【答案】D
【解析】,,的几何意义是以原点为圆心,半径为的圆的面积的,故,故选D.
二、填空题
23.已知定义在上的函数与,若函数为偶函数,函数为奇函数,且,则__________.
【答案】12.
【解析】分析:根据定积分的几何意义和函数的奇偶性求解.
详解:∵函数为偶函数,函数为奇函数,
∴函数的图象关于y轴对称,函数的图象关于原点对称.
∴,,
∴.
点睛:定积分的几何意义是表示曲线以下、x轴以上和直线之间的曲边梯形的面积,解题时要注意面积非负,而定积分的结果可以为负.
24.若,则在的展开式中,的系数是__________.(用数字作答)
【答案】84
点睛:本题考点是定积分,以及二项展开式的通项公式是解决二项展开式特殊项问题的方法.
25.已知椭圆的焦点为,,其中,直线与椭圆相切于第一象限的点,且与,轴分别交于点,,设为坐标原点,当的面积最小时,,则此椭圆的方程为__________.
【答案】
【解析】分析:先根据定积分求出c,由题意,切线方程为
利用基本不等式,结合(为坐标原点)的面积最小,可得切点坐标,利用三角形的面积公式,即可求出 ,问题得以解决.
详解:
由椭圆的焦点为 ,可设椭圆的方程为
直线与椭圆相切,则切线方程为
点睛:本题考查三角形面积的计算,考查直线与椭圆是位置关系,考查余弦定理的运用,基本不等式,椭圆的切线方程,属于难题
26.已知展开式中的常数项为60,则__________.
【答案】4.
【解析】分析:的通项公式为,令,,于是,利用微积分定理求解即可.
详解:的通项公式为,
令,,
,故答案为.
点睛:本题主要考查定积分以及二项展开式定理的通项与系数,属于中档题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.
27.已知,则二项式的展开式中的系数为__________.
【答案】-160
点睛:本题主要考查定积分的计算,考查利用二项式的展开式求指定项.意在考查学生对这些基础知识的掌握能力和基本运算能力.
28.若(其中),则的展开式中的系数为__________.
【答案】280
【解析】分析:利用微积分基本定理,求得,可得二项展开式通项为令得进而可得结果.
详解:因为 ,
所以,展开式的通项为
令得
所以,的展开式中的系数为,
故答案为.
点睛:本题主要考查二项展开式定理的通项与系数,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.
29.已知抛物线的焦点坐标为,则抛物线与直线
所围成的封闭图形的面积为__________.
【答案】
30.已知,则二项式展开式中的常数项是__________.
【答案】
【解析】,
展开式通项为,
令,,∴常数项为.
故答案为240.
31.已知函数是定义在上的奇函数,则__________.
【答案】
【解析】 .
32.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为 的圆面,中间有边长为的正方形孔,若随机向铜钱上滴一滴油,则油滴整体(油滴是直径为0.2的球)正好落入孔中的概率是__________.
【答案】
【解析】因为直径为的圆中有边长为的正方形,由几何概型的概率公式,得“正好落入空中”的概率为.
33.已知函数,则__________.
【答案】
点睛:定积分的计算一般有三个方法:
(1)利用微积分基本定理求原函数;
(2)利用定积分的几何意义,利用面积求定积分;
(3)利用奇偶性对称求定积分,奇函数在对称区间的定积分值为0
34.若,则__________.
【答案】3
【解析】 , ,则.
35.若,且,则的值为__________.
【答案】1
点睛:求解这类问题要注意:①区别二项式系数与展开式中项的系数,灵活利用二项式系数的性质;②根据题目特征,恰当赋值代换,常见的赋值方法是使得字母因式的值或目标式的值为1,-1.
36.如图所示,在平面直角坐标系内,四边形为正方形且点坐标为.抛物线的顶点在原点,关于轴对称,且过点.在正方形内随机取一点,则点在阴影区域内的概率为_________.
【答案】
【解析】由抛物线的顶点在原点,关于轴对称,且过点,所以抛物线方程为,
阴影区域的面积为,正方形的面积为1,
点在阴影区域内的概率为.
故答案为:
37.计算__________.
【答案】4
【解析】由题意得,
38.如图,在长方形内任取一点,则点落在阴影部分内的概率为__________.
【答案】
【解析】将代入 ,得 ,所以阴影部分面积为 ,矩形面积为 ,所以点 落在阴影部分内的概率为 ,故答案为 .
39.如图所示,由直线, 及轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即.类比之,若对,不等式 恒成立,则实数等于__________.
【答案】2
40.已知函数,则__________;
【答案】
【解析】,
而, 表示半圆的面积,即,则.
点睛:本题考查微积分基本定理、定积分的几何意义;求定积分的值主要有两种方法:
(1)利用微积分基本定理求解,即找出函数的原函数进行求解,即;
(2)利用函数的几何意义进行求解,主要涉及的定积分,如表示,即半圆的面积.
41.__________.
【答案】
42.已知实数满足不等式组且的最大值为,则__________.
【答案】
【解析】
作出可行域,目标函数可变为,令,作出,由平移可知直线过时取最大值,则.则.故本题应填.
43.我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系平面内,若函数的图象与轴围成一个封闭的区域,将区域沿轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域的面积相等,则此圆柱的体积为__________.
【答案】
【解析】由题可得:底面面积为,所以圆柱得体积为:
44.若正实数满足,则的最小值为_______.
【答案】2
【解析】因为,所以,即,所以,故,应填答案。
45.若的展开式中项的系数为4,则________________
【答案】
点睛:求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第项,再由特定项的特点求出值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第项,由特定项得出值,最后求出其参数.
46.如图,圆内的正弦曲线, 与轴围成的区域记为(图中阴影部分),随机向圆内投一个点,则点落在区域外的概率是__________.
【答案】
【解析】阴影部分的面积=,圆的面积为,所以点落在区域外的概率是
点睛:本题的关键是利用定积分求出阴影区域的面积,然后根据几何概型的计算公式求解即可
三、解答题
47.设点在曲线上,从原点向移动,如果直线,曲线及直线所围成的两个阴影部分的面积分别记为,,如图所示.
(1)当时,求点的坐标;
(2)当有最小值时,求点的坐标.
【答案】(1);(2).
点睛:本题主要考查了定积分的应用及利用导数求解函数的最值问题,着重考查了分析问题和解答问题的能力,以及推理与运算能力.
48.如图,函数(其中)的图像与坐标轴的三个交点为,且,,为的中点,且的纵坐标为.
(1)求的解析式;
(2)求线段与函数图像围成的图中阴影部分的面积.
【答案】(1);(2)
【解析】分析:(1)由,则周期,
又,则,故,从而可得结果;(2)将阴影部分的面积分成两部分,分别利用定积分的几何意义求的曲边形的面积,求和即可.
详解:(1)由,则周期
又
点睛:本题主要考查三角函数的图象与性质以及定积分的几何意义,属于中档题.一般情况下,定积分的几何意义是介于轴、曲线 以及直线之间的曲边梯形面积的代数和 ,其中在轴上方的面积等于该区间上的积分值,在
轴下方的面积等于该区间上积分值的相反数,所以在用定积分求曲边形面积时,一定要分清面积与定积分是相等还是互为相反数;两条曲线之间的面积可以用两曲线差的定积分来求解.
49.已知二次函数,直线,直线(其中,为常数),若直线与函数的图象以及轴与函数的图象所围成的封闭图形(阴影部分)如图所示.
(1)求的值;
(2)求阴影面积关于的函数的解析式.
【答案】(1);(2).
【解析】试题分析:(1)由图象可知函数图象过点,并且的最大值为,分别代入解析式可得关于的方程组,即可解得的值;(2)先求出直线(其中为常数)与拋物线的交点横坐标(用表示),再利用定积分的几何意义求两部分面积之和即可.
试题解析:(1)由图形可知二次函数的图象过点,,并且的最大值为,则
,解得,
∴函数的解析式为.
50.抛物线y2=x与直线x-2y-3=0的两个交点分别为P、Q,点M在抛物线上从P向Q运动(点M不同于点P、Q),
(Ⅰ)求由抛物线y2=x与直线x-2y-3=0所围成的封闭图形面积;
(Ⅱ)求使⊿MPQ的面积为最大时M点的坐标。
【答案】(1) (2)P点的坐标为(1,1)时,⊿PAB的面积最大
【解析】试题分析:(1)先求直线与抛物线交点,确定上下函数,分两种情况求定积分,即得面积(2)过点M的切线与直线x-2y-3=0平行时⊿MPQ的面积为最大,利用导数几何意义求出切点M坐标
试题解析:
解:
方法二 若选取积分变量为y,则两个函数分别为x=y2
,x=2y+3.由方法一知上限为3,下限为-1.
∴S=dy=(y2+3y-y3) =(9+9-9)-(1-3+)=.
(Ⅱ)设点M的坐标为(a, b),要使⊿MPQ的面积最大即使点M到直线x-2y-3=0的距离最大 ,故过点M的切线与直线x-2y-3=0平行,故过点M的切线斜率为K=1/2, a=1,b=1,∴P点的坐标为(1,1)时,⊿PAB的面积最大。
点睛:1.求曲边图形面积的方法与步骤
(1)画图,并将图形分割为若干个曲边梯形;
(2)对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;
(3)确定被积函数;
(4)求出各曲边梯形的面积和,即各积分的绝对值的和.
2.利用定积分求曲边图形面积时,一定要找准积分上限、下限及被积函数.当图形的边界不同时,要分不同情况讨论.