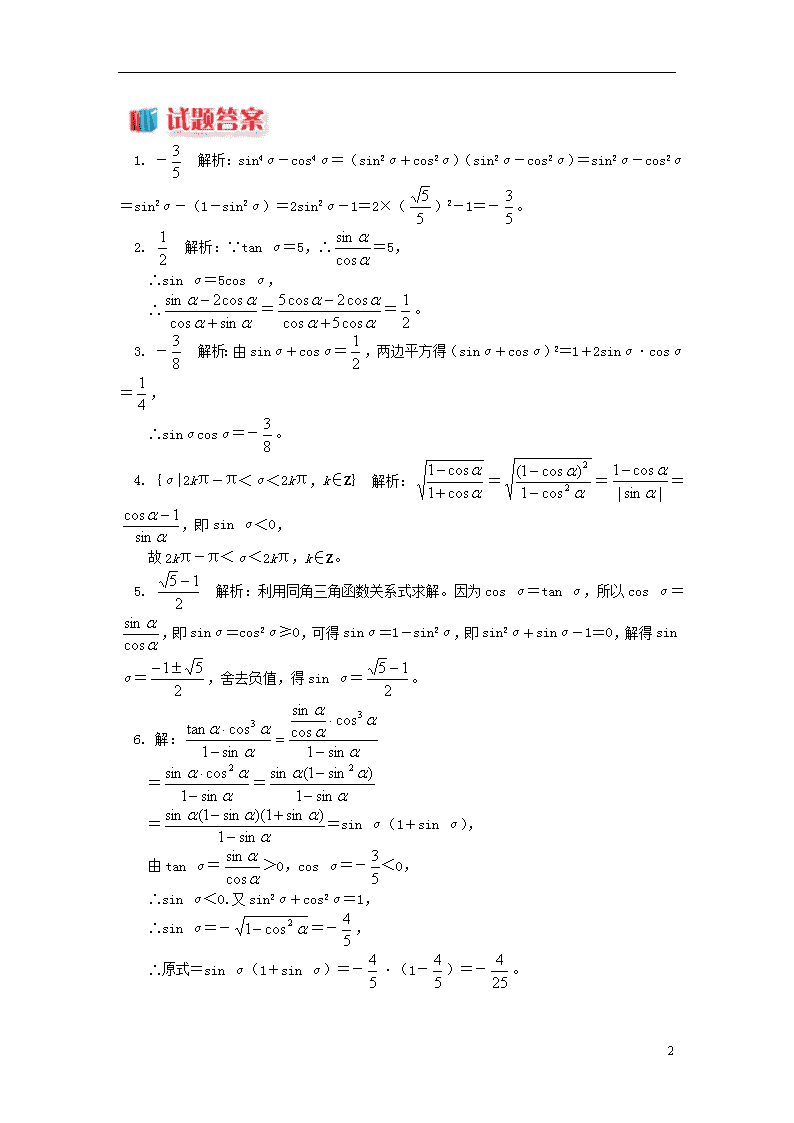2020高中数学 第一章 三角函数 3页

同角三角函数函数关系 ‎（答题时间：40分钟）‎ ‎**1. 已知sin α＝，则sin4α－cos4α的值是________。‎ ‎*2. （连云港高一检测）已知tan α＝5，则＝________。‎ ‎*3. 已知sin α＋cos α＝，则sin αcos α＝________。‎ ‎**4. 使＝成立的α的集合是________。‎ ‎5. 已知cos α＝tan α，则sin α＝________。‎ ‎**6. 若cos α＝－且tan α＞0，求的值。‎ ‎**7. 证明：＝cos2x－sin2x。‎ ‎***8. 已知sin α，cos α是关于x的二次方程2x2＋（＋1）x＋m＝0的两根，求2tanα·的值。‎ 3‎ ‎1. － 解析：sin4α－cos4α＝（sin2α＋cos2α）（sin2α－cos2α）＝sin2α－cos2α＝sin2α－（1－sin2α）＝2sin2α－1＝2×（）2－1＝－。‎ ‎2. 解析：∵tan α＝5，∴＝5，‎ ‎∴sin α＝5cos α，‎ ‎∴＝＝。‎ ‎3. － 解析：由sinα＋cosα＝，两边平方得（sinα＋cosα）2＝1＋2sinα·cosα＝，‎ ‎∴sinαcosα＝－。‎ ‎4. {α|2kπ－π＜α＜2kπ，k∈Z} 解析：＝＝＝，即sin α＜0，‎ 故2kπ－π＜α＜2kπ，k∈Z。‎ ‎5. 解析：利用同角三角函数关系式求解。因为cos α＝tan α，所以cos α＝，即sin α＝cos2α≥0，可得sin α＝1－sin2α，即sin2α＋sin α－1＝0，解得sin α＝，舍去负值，得sin α＝。‎ ‎6. 解：‎ ‎＝＝‎ ‎＝＝sin α（1＋sin α），‎ 由tan α＝＞0，cos α＝－＜0，‎ ‎∴sin α＜0.又sin2α＋cos2α＝1，‎ ‎∴sin α＝－＝－，‎ ‎∴原式＝sin α（1＋sin α）＝－·（1－）＝－。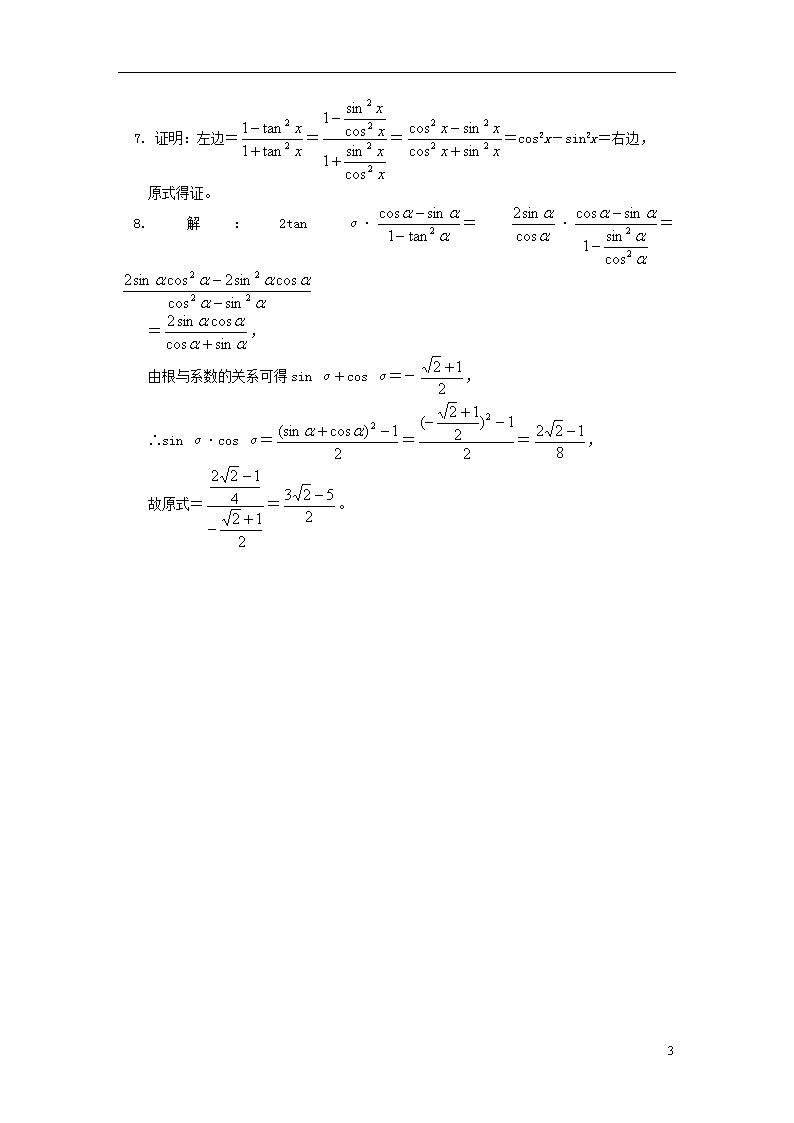‎ 3‎ ‎7. 证明：左边＝＝＝＝cos2x－sin2x＝右边，‎ 原式得证。‎ ‎8. 解：2tan α·＝·＝‎ ‎＝，‎ 由根与系数的关系可得sin α＋cos α＝－，‎ ‎∴sin α·cos α＝＝＝，‎ 故原式＝＝。‎ 3‎