数学理卷·2018届河北省武邑中学高三下学期期中考试（2018 11页

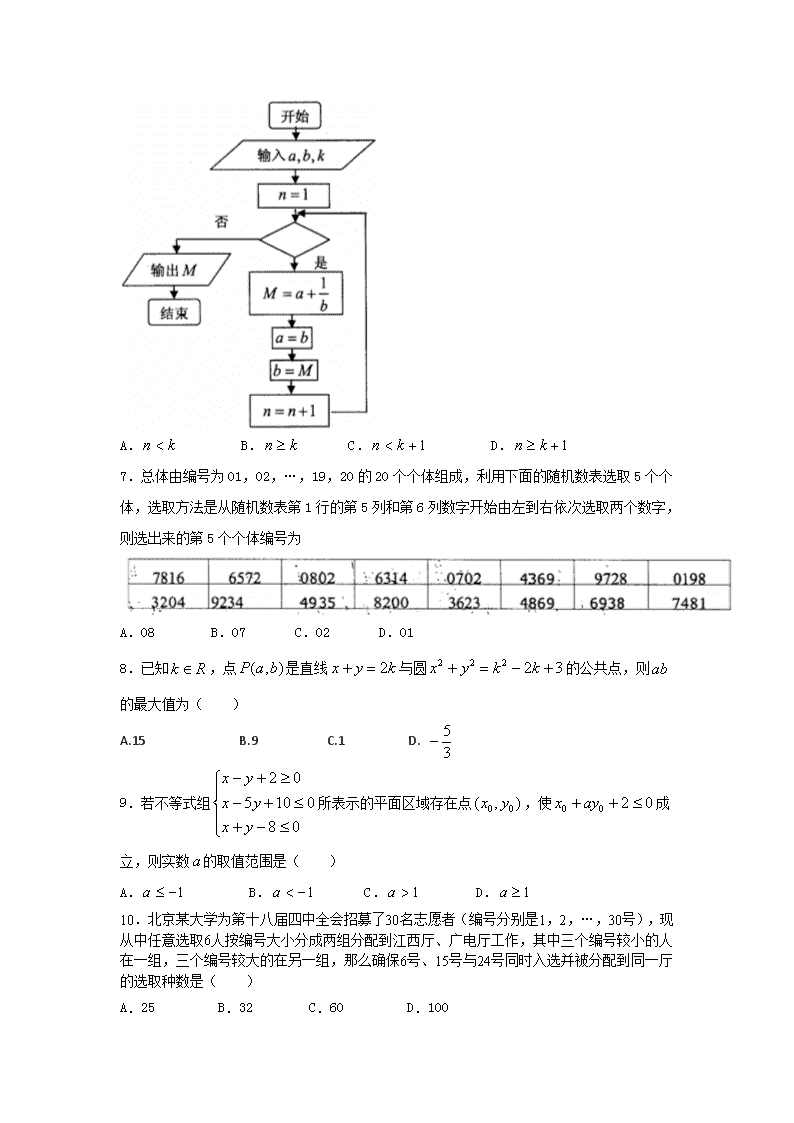
河北省武邑中学2018届高三下学期期中考试 数学（理）试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则（ ）‎ A． B． C． D．‎ ‎2．已知实数满足，则（ ）‎ A． B． C． D． ‎ ‎3．给出下列命题：‎ ‎①已知，“且”是“”的充分条件；‎ ‎②已知平面向量，“”是“”的必要不充分条件；‎ ‎③已知，“”是“”的充分不必要条件；‎ ‎④命题：“，使且”的否定为：“，都有且”.其中正确命题的个数是（ ）‎ A．0 B．1 C．2 D．3 ‎ ‎4．若定义在上的偶函数满足，且当时，，则函数的零点个数是（ ）‎ A．6个 B．4个 C．3个 D．2个 ‎ ‎5．设函数，其中常数满足.若函数（其中是函数的导数）是偶函数，则等于（ ）‎ A． B． C． D．‎ ‎6．执行如图的程序框图，如果输入的分别为，输出的，那么判断框中应填入的条件为（ ）‎ A． B． C． D．‎ ‎7．总体由编号为01，02，…，19，20的20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体编号为 A．08 B．07 C．02 D．01‎ ‎8．已知，点是直线与圆的公共点，则的最大值为（ ）‎ A.15 B.9 C.1 D. ‎ ‎9．若不等式组所表示的平面区域存在点，使成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎10．北京某大学为第十八届四中全会招募了30名志愿者（编号分别是1，2，…，30号），现从中任意选取6人按编号大小分成两组分配到江西厅、广电厅工作，其中三个编号较小的人在一组，三个编号较大的在另一组，那么确保6号、15号与24号同时入选并被分配到同一厅的选取种数是（ ）‎ A．25 B．32 C．60 D．100‎ ‎11．已知在中，两直角边，，是内一点，且，设，则（ ）‎ A． B． C．3 D．‎ ‎12．已知函数的定义域为，若对于分别为某个三角形的边长，则称为“三角形函数”.给出下列四个函数：‎ ‎①；②；③；④.其中为“三角形函数”的个数是（ ）‎ A．1 B．2 C．3 D．4‎ 二、填空题（每题4分，满分20分，将答案填在答题纸上）‎ ‎13．若满足约束条件，则的最小值是 .‎ ‎14．若的展开式中的系数是80，则实数的值是 .‎ ‎15．已知几何体的三视图如图所示，其中俯视图为一正方形，则该几何体的表面积为 . ‎ ‎16．若函数的图象上存在不同的两点，，其中使得的最大值为0，则称函数是“柯西函数”.‎ 给出下列函数：‎ ‎①；②；③；④.‎ 其中是“柯西函数”的为 . ‎ 三、解答题 （本大题共6题，共70分．解答应写出文字说明、证明过程或演算步骤．） ‎ ‎17．已知数列的前项和为，且满足.‎ ‎（1）求数列的通项公式；‎ ‎（2）令，记数列的前项和为，证明：.‎ ‎18．高二某班共有20名男生，在一次体检中这20名男生被平均分成两个小组，第一组和第二组男生的身高（单位：cm）的茎叶图如下：‎ ‎（1）根据茎叶图，分别写出两组学生身高的中位数；‎ ‎（2）从该班身高超过180cm的7名男生中随机选出2名男生参加篮球队集训，求这2名男生至少有1人来自第二组的概率；‎ ‎（3）在两组身高位于（单位：cm）的男生中各随机选出2人，设这4人中身高位于（单位：cm）的人数为，求随机变量的分布列和数学期望.‎ ‎19．菱形的对角线与交于点，，点分别在上，，交于点，将沿折到位置，.‎ ‎（1）证明：平面；‎ ‎（2）求二面角的正弦值.‎ ‎20．设抛物线的准线与轴交于，抛物线的焦点，以为焦点，离心率的椭圆与抛物线的一个交点为；自引直线交抛物线于两个不同的点，设.‎ ‎（1）求抛物线的方程椭圆的方程；‎ ‎（2）若，求的取值范围.‎ ‎21．已知函数.‎ ‎（1）设，求函数的单调区间；‎ ‎（2）若，设为函数图象上不同的两点，且满足，设线段中点的横坐标为，证明：.‎ 请考生在22、23二题中任选一题作答，如果都做，则按所做的第一题记分.‎ ‎22．选修4-4：坐标系与参数方程 已知直线的参数方程为（为参数，），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，射线，，分别与曲线交于三点（不包括极点）.‎ ‎（1）求证：； ‎ ‎（2）当时，若两点在直线上，求与的值.‎ ‎23．选修4-5：不等式选讲 已知函数.‎ ‎（1）当，解不等式；‎ ‎（2）若，且当时，不等式恒成立，求实数的取值范围.‎ 数 学（理科）参考答案 ‎ ‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎ ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A C B A C D B A C A C ‎ ‎ 二、填空题：本大题共4小题，每小题5分，共20分. 把答案填在答题卡中对应题号后的横线上.‎ ‎ 13．　　　　　14．2 　　　　15．　　　　　　16．①④‎ 三、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤.‎ ‎17．解：(1)当时，有，解得，‎ 当时，有，则 整理得 ‎∴数列是以为公比，以为首项的等比数列 ‎∴.‎ ‎（2）由（1）有，则 ‎∴‎ 易知数列为递增数列，‎ ‎∴，即.‎ ‎18．(1) 第一组学生身高的中位数为，‎ 第二组学生身高的中位数为；‎ ‎（2）记“这2名男生至少有1人来自第二组”为事件，‎ ‎，‎ ‎∴这2名男生至少有1人来自第二组的概率为；‎ ‎（3）的所有可能取值是0，1，2，3‎ ‎，，，‎ 的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎.‎ ‎19．解：(1)∵，‎ ‎∴，∴，‎ ‎∵四边形为菱形，‎ ‎∴，‎ ‎∴，∴，∴‎ ‎∵，‎ ‎∴；‎ 又，，∴，∴，∴，‎ ‎∴，∴，又∵，‎ ‎∴平面.‎ ‎（Ⅱ）建立如图所示的空间直角坐标系：‎ ‎，‎ ‎，‎ 设平面的一个法向量为，‎ 由得，取，‎ ‎∴，同理可得平面的法向量为，‎ ‎∴，∴.‎ ‎20.解：(1)设椭圆的标准方程为，‎ 由题意得，解得 ‎∴椭圆的方程为 ‎∴点的坐标为，‎ ‎∴，∴抛物线的方程是 ‎ (2)由题意得直线的斜率存在，设其方程为，‎ 由消去整理得（）‎ ‎∵直线与抛物线交于两点，‎ ‎∴，‎ 设，则①，②，‎ ‎∵，‎ ‎∴‎ ‎∴，③‎ 由①②③消去得.‎ ‎∴‎ ‎，即，将代入上式得，‎ ‎，‎ ‎∵在上单调递减，‎ ‎∴，即，‎ ‎∴，‎ ‎∴，即的取值范围为.‎ ‎21．解：(1) ,‎ ‎①时， 定义域为 当时，，故在上单调递减；‎ 当时，，故在上单调递增；‎ ‎②时，定义域为 当时，，故在上单调递增；‎ 当时，，故在上单调递减.‎ ‎（2）‎ ‎，故在定义域上单调递增，‎ 只需证：，，‎ 不妨设 则 ‎，‎ 从而在上单调递减，故，即（）式.‎ ‎22.解：(1)证明：依题意，，‎ ‎，，‎ 则 ‎（2）当时，两点的极坐标分别为，‎ 化为直角坐标，，‎ 经过点的直线方程为，‎ 又直线经过点，倾斜角为，故，.‎ ‎23.解：(1) 当时，，则 由解得或，即原不等式的解集为.‎ ‎（2），即，又且 所以，且 所以即 令，则，‎ 所以时， ，‎ 所以，解得，‎ 所以实数的取值范围是. ‎