THUSSAT中学生标准学术能力诊断性测试2020年1月诊断性测试文科数学试卷 6页

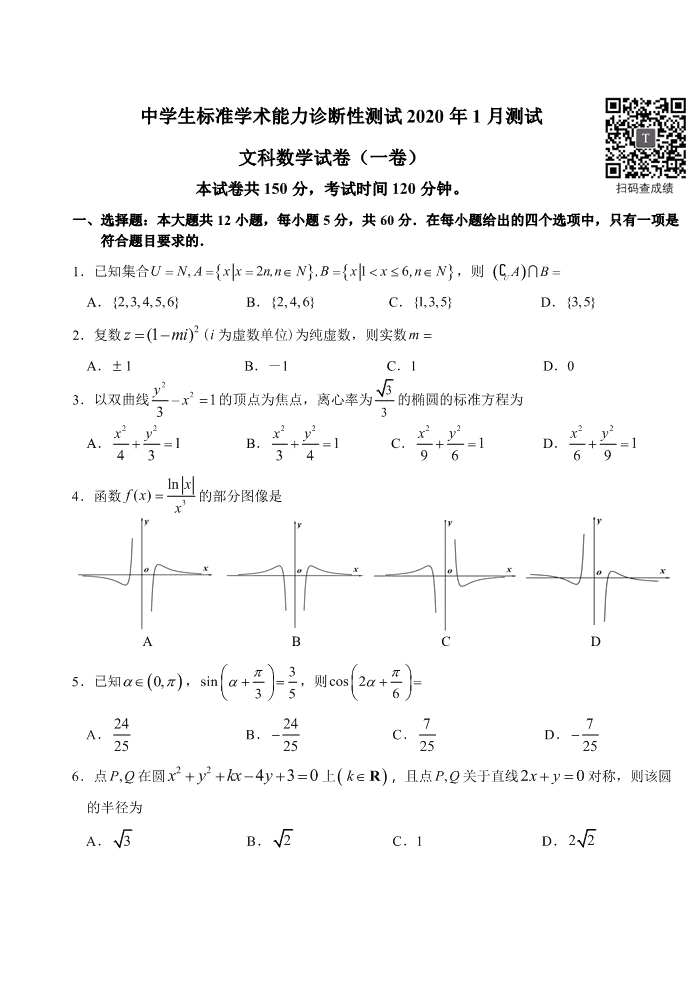
中学生标准学术能力诊断性测试 2020 年 1 月测试 文科数学试卷（一卷） 本试卷共 150 分，考试时间 120 分钟。 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．已知集合  , 2 1 6U N A x x n,n N ,B x x n N= = =  =   , ，则 ( )U AB= A． { 2 ,3 , 4 ,5 ,6 } B． { 2, 4, 6 } C． {1,3,5} D． {3 ,5} 2．复数 2(1 )z m i=− (i 为虚数单位)为纯虚数，则实数 m = A．  1 B．－1 C．1 D．0 3．以双曲线 2 2 1 3 y x−=的顶点为焦点，离心率为 3 3 的椭圆的标准方程为 A． 22 1 43 xy+= B． 22 1 34 xy+= C． 22 1 96 xy+= D． 22 1 69 xy+= 4．函数 3 ln() xfx x = 的部分图像是 A B C D 5．已知 ( )0, ， 3sin 35  += ，则 cos 2 6  += A． 24 25 B． 24 25 − C． 7 25 D． 7 25 − 6．点 ,PQ在圆 22 4 3 0x y kx y+ + − + = 上( )Rk  ，且点 ,PQ关于直线 20xy+=对称，则该圆 的半径为 A． 3 B． 2 C．1 D． 22 7．已知函数 ( ) 3f x x x=−和点 ( )11P −， ，则过点 P 与该函数图像相切的直线条数为 A．1 B．2 C．3 D．4 8．某几何体的三视图如图所示（单位：cm），则该几何体的体积是 A． 37 cm 2 B． 37 cm 3 C． 37 cm 6 D． 37c m 9．已知数列  na 是等比数列，前 n 项和为 nS ，则“ 3 1 52a a a+”是“ 21 0nS −  ”的 A．必要不充分条件 B．充分不必要条件 C．充要条件 D．既不充分也不必要条件 10．在 OAB△ 中，已知 2, 1, 45|= | |=|OB AB AOB =∠ ，点 P 满足 ( , )ROP OA OB=+  ，其 中 ,满足 23+= ，则 ||OP 的最小值为 A． 35 5 B． 25 5 C． 6 3 D． 6 2 11．边长为 2 的等边 ABC△ 和有一内角为 30 的直角 1ABC△ 所在半平面构成 60 的二面角，则下 列不可能是线段 1CC 的取值的是 A． 30 3 B． 10 C． 10 2 D． 10 3 12．已知不等式 1ln a xx a x x e + +  对 ( )1x, + 恒成立，则实数 a 的最小值为 A． e− B． 2 e− C． e− D． 2e− 俯视图 侧视图正视图 22 1 11 13．如图所示的程序框图的输出值 ( 0 ,1y  ，则输入值 x  ． 14．在 ABC△ 中， 2 s in c o s ( ) 6 b A a B =−, 2b = ，若满足条件的 ABC△ 有且仅有一个，则实数 a 的取值范围是 ． 15．过点 (1,1)P 作直线 l 与双曲线 2 2 2 yx λ−=交于 ,AB两点，若点 P 恰 为线段 AB 的中点，则实数  的取值范围是 ． 16．如图，正三角形 ABC 边长为 2， D 是线段 BC 上一点，过 C 点作直线 AD 的垂线，交线段 AD 的延长线于点 E ，则 A D D E 的最大值 为 ． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每道试 题考生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：60 分． 17．（ 12 分）根据某省的高考改革方案，考生应在 3 门理科学科（物理、化学、生物）和 3 门文科 学科（历史、政治、地理）的 6 门学科中选择 3 门学科参加考试。根据以往统计资料，1 位同学 选择生物的概率为 0.5，选择物理但不选择生物的概率为 0.2，考生选择各门学科是相互独立的． （1）求 1 位考生至少选择生物、物理两门学科中的 1 门的概率； （2）某校高二段 400 名学生中，选择生物但不选择物理的人数为 140，求 1 位考生同时选择生 物、物理两门学科的概率． （第 16 题图） (第 13 题图) 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 18．（12 分）设数列 na 是公差不为零的等差数列，其前 n 项和为 nS , 1 1a = ．若 1 2 5,,a a a 成等比数 列． （1）求 na 及 nS ； （2）设 2 1 1 1n n b a + = − ()nN ，求数列 nb 前 n 项和 nT ． 19．（12 分）如图，四棱锥 -P ABCD 中， AP ⊥ 平面 PCD , //AD BC , 2DAB =, （第 19 题图） 1 2 A P A B B C A D= = = , E 为 AD 的中点， AC 与 BE 相交于点 O ． （1）求证： P O A B C D⊥ 平面 ； （2）求 AB 与平面 PBD 所成角 的正弦值． 20．（12 分）已知 ( ) l nf x x = , ()g x x = ． （1）若 ( ) ( ) () af x g x gx +在 (0 ,1] 恒成立，求实数 a 的取值范围； （2）若 m , 0n  , 1mn+=，求证 221( ) ( ) [ ( )] [ ( )] 4 f m f n g m g n−． 21．（ 12 分）如图，已知圆 ( ) ( )222 2 1Q x y+ + − =： ，抛物线 2:4C y x = 的焦点为 F，过 F 的直线 l 与抛物线 C 交于 ,AB两点，过 F 且与 l 垂直 的直线 l  与圆 Q 有交点． （1）求直线 l  的斜率的取值范围； （2）求 AOB△ 面积的取值范围． （第 19 题图） （第 21 题图） （第 21 题图） （二）选考题：共 10 分．请考生在第 22,23 题中任选一题作答，如果多做， 则按所做的第一题计分．作答时请写清题号． 22．[选修 4−4：坐标系与参数方程]（10 分） 在平面直角坐标系 x O y 中，曲线 1C 的参数方程为 1 2cos 3 2sin x α y α =+ = − +    （其中  为参数, R  ）．在极 坐标系（以坐标原点 O 为极点，以 轴非负半轴为极轴）中，曲线 2C 的极坐标方程为 sin 6 πρ θ a−= ． （1）求曲线 1C 的普通方程和曲线 2C 的直角坐标方程； （2）若曲线 1C 上恰有一个点到曲线 2C 的距离为 1，求曲线 2C 的直角坐标方程． 23．[选修 4−5：不等式选讲]（10 分） （1）解不等式 1 2 5 3 2 2 0xx+ − − + −  ； （2）求函数 3 2 4 2 3y x x= − + − 的最大值． x