- 518.00 KB
- 2021-06-03 发布
太原五中2017-2018学年度第二学期阶段性练习
高 三 数 学(文)
命题、校对:凌 河(2018.3.28)
一、选择题(本大题共12小题,每小题5分,共60分,每小题有且只有一个正确选项)
1.已知全集,,,则( )
A. B. C. D.
2.已知为虚数单位,若复数在复平面内对应的点在第四象限,
则的取值范围为( )
A. B. C. D.
3.从编号为1,2,…,79,80的80件产品中,采用系统抽样的方法抽取容量为5的样本,若编号为10的产品在样本中,则该样本中产品的最大编号为( )
A.72 B.73 C.74 D.75
4.,,,则( )
A. B. C. D.
5.下列叙述中正确的是( )
A.命题“,”的否定是“”;
B.命题“若,则”的否命题是“若,则”;
C.在区间上随机取一个数,则事件“”发生的概率为;
D.“命题为真”是“命题为真”的充分不必要条件.
6.已知满足对,且时,(为常数),则的值为( )
A.4 B.-4 C.6 D.-6
7.某几何体的三视图如图所示,若该几何体的体积为,
则它的表面积是( )
A. B.
C. D.
8.若倾斜角为的直线与曲线相切于点,
则的值为( )
A. B. 1
C. D.
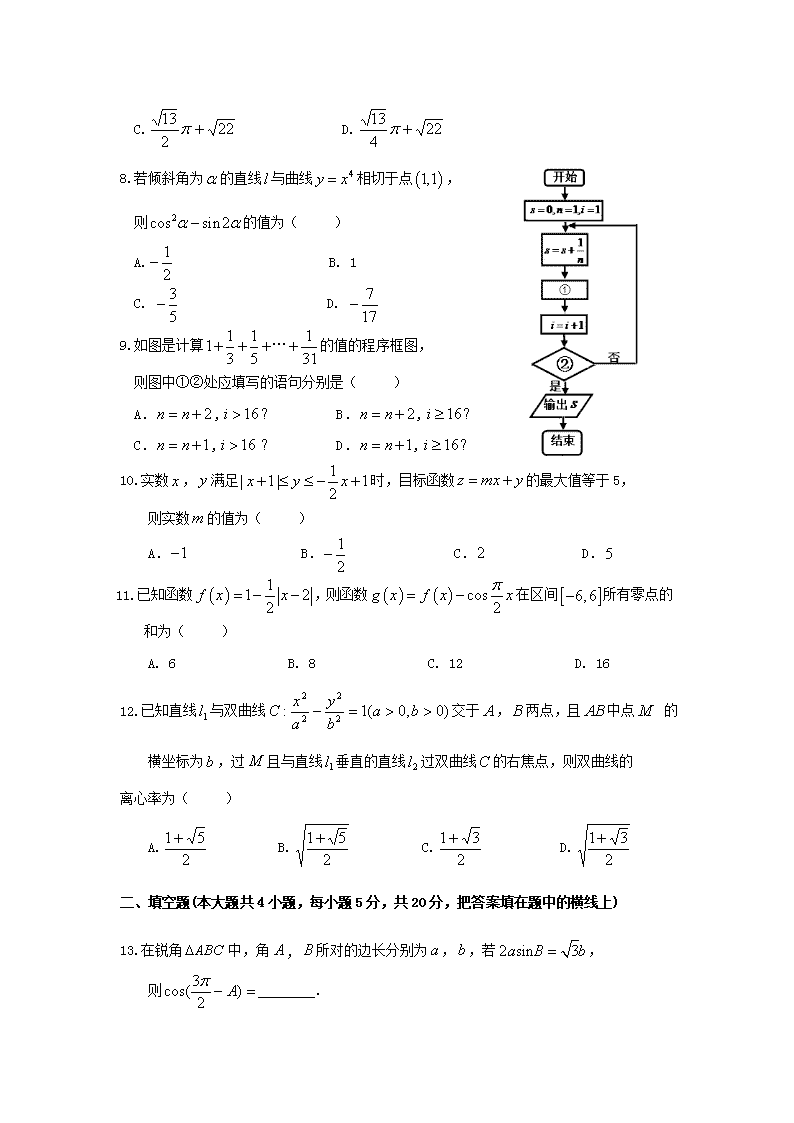
9.如图是计算的值的程序框图,
则图中①②处应填写的语句分别是( )
A., B.,
C., D.,
10.实数,满足时,目标函数的最大值等于5,
则实数的值为( )
A. B. C. D.
11.已知函数,则函数在区间所有零点的和为( )
A. 6 B. 8 C. 12 D. 16
12.已知直线与双曲线交于,两点,且中点 的横坐标为,过且与直线垂直的直线过双曲线的右焦点,则双曲线的
离心率为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.在锐角中,角,所对的边长分别为,,若,
则 .
14.已知点,,若圆上存在点
使,则的最小值为 .
15.若,都是正数,且,则的最小值为_______.
16.已知三棱锥的体积为,且底面,且的面积为,
三边,,的乘积为,则三棱锥的外接球的表面积为________.
三、解答题(本大题5小题,共60分,解答应写出文字说明、证明过程或演算步骤)
17.(12分)已知.
(1)若是等差数列,且,,求;
(2)若是等比数列,且,,求.
18.(12分)某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(1)求这次铅球测试成绩合格的人数;
(2)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;
(3)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,
随机选出2人参加“毕业运动会”,已知、的成绩均为优秀,求两人至少有1人入选的概率.
19.(12分)如图,在长方体中,分别为
的中点,是上一个动点,且.
(1)当时,求证:平面平面;
(2)是否存在,使得?若存在,请求出的值;
若不存在,请说明理由.
20.(12分)
已知椭圆:的离心率为,且过点,动直线:交椭圆于不同的两点,,且(为坐标原点)
(1)求椭圆的方程.
(2)讨论是否为定值?若为定值,求出该定值,若不是请说明理由.
21.(12分)已知函数(其中是自然对数的底数)
(1)若,当时,试比较与的大小;
(2)若函数有两个极值点,
求的取值范围,并证明:.
说明:请在22、23题中任选一题做答,写清题号.如果多做,则按所做第一题记分.
22.(10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线(为参数,实数),曲线(为参数,实数).在以为极点,轴的正半轴为极轴的极坐标系中,射线与交于两点,与交于两点. 当时,;当时,.
(1)求,的值;
(2)求的最大值.
23.(10分)选修4-5:不等式选讲
设函数(,实数).
(1)若,求实数的取值范围;
(2)求证:.