上海交通大学附属中学2019-2020学年度第二学期高三数学考前测试卷 9页

‎ ‎ 上海交通大学附属中学2019-2020学年度第二学期 高三数学考前测试卷 一、填空题 ‎1．已知集合，，则______.‎ ‎2．函数的最小正周期是______.‎ ‎3．抛物线的准线方程是______.‎ ‎4．已知方程的一个根是（其中，是虚数单位），则实数______.‎ ‎5．设满足约束条件，则的最小值是______.‎ ‎6．若是展开式中项的系数，则______.‎ ‎7．在我国古代数学名著《九章算术》中，将四个面都为直角三角形的四面体称为鳖儒。如图，在鳖臑中，平面，其三视图是三个全等的等腰直角三角形，则异面直线与所成的角的余弦值为______.‎ ‎8．为抗击此次疫情，我市某医院从3名呼吸内科医生、4名急诊重症科医生和5名护士中选派5人组成一个抗击疫情医疗小组，则呼吸内科与急诊重症科医生都至少有一人的选派方法种数是_______.‎ ‎9．若关于的方程的解集为空集，求实数的取值范围______.‎ ‎10．已知函数为定义域上的奇函数，且在上是单调递增函数，函数，数列为等差数列，且公差不为0，若，则______.‎ ‎ ‎ ‎11．已知整数数列共5项，其中，，且对任意，都有，则符合条件的数列个数为______.‎ ‎12．已知点，椭圆上两点、满足，则的最大值为______.‎ 二、选择题 ‎13．“”是“”的（ ）‎ A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分又非必要条件 ‎14．已知为抛物线的焦点，、是抛物线上的不同两点，则下列条件中与“、、三点共线”等价的是（ ）‎ A． B． C． D．‎ ‎15．已知曲线的参数方程为，其中参数，则曲线（ ）‎ A．关于轴对称 B．关于轴对称 C．关于原点对称 D．没有对称性 ‎16．已知数列与前项和分别为、，且，，，，对任意的，恒成立，则的最小值是（ ）‎ A．1 B． C． D．‎ 三、解答题 ‎17．如图，四棱锥的底面是边长为1的菱形，，，平面，、分别是、的中点.‎ ‎（1）求证：直线平面；‎ ‎（2）求点到平面的距离.‎ ‎ ‎ ‎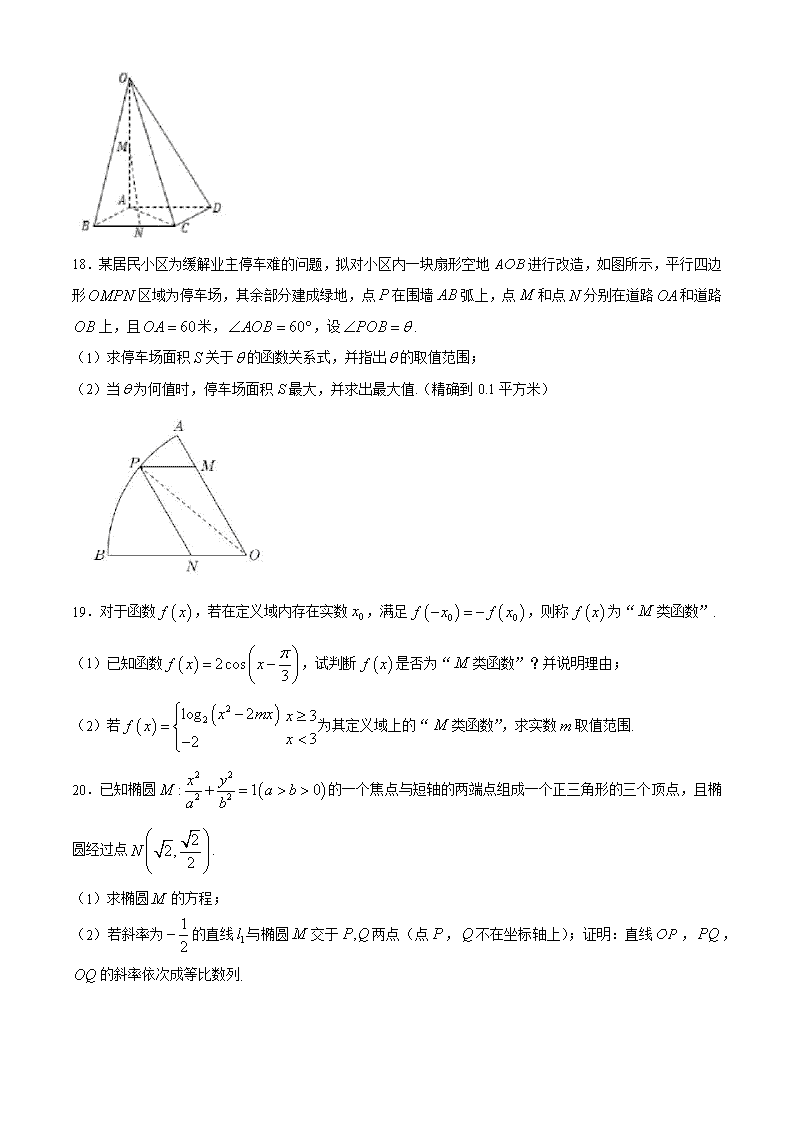18．某居民小区为缓解业主停车难的问题，拟对小区内一块扇形空地进行改造，如图所示，平行四边形区域为停车场，其余部分建成绿地，点在围墙弧上，点和点分别在道路和道路上，且米，，设.‎ ‎（1）求停车场面积关于的函数关系式，并指出的取值范围；‎ ‎（2）当为何值时，停车场面积最大，并求出最大值.（精确到0.1平方米）‎ ‎19．对于函数，若在定义域内存在实数，满足，则称为“类函数”.‎ ‎（1）已知函数，试判断是否为“类函数”？并说明理由；‎ ‎（2）若为其定义域上的“类函数”，求实数取值范围.‎ ‎20．已知椭圆的一个焦点与短轴的两端点组成一个正三角形的三个顶点，且椭圆经过点.‎ ‎（1）求椭圆的方程；‎ ‎（2）若斜率为的直线与椭圆交于两点（点，不在坐标轴上）；证明：直线，，的斜率依次成等比数列.‎ ‎ ‎ ‎（3）设直线与椭圆交于两点，且以线段为直径的圆过椭圆的右顶点，求面积的最大值.‎ ‎21．已知是定义在上的函数，满足：①对任意，均有；②对任意，均有.数列满足：，，.‎ ‎（1）若函数，求实数的取值范围；‎ ‎（2）若函数在上单调递减，求证：对任意正实数，均存在，使得时，均有；‎ ‎（3）求证：“函数在上单调递增”是“存在，使得”的充分非必要条件.‎ 上海交通大学附属中学2019-2020学年度第二学期 高三数学考前测试卷参考答案 一、填空题 ‎1． 2．‎ ‎3． 4．5‎ ‎5．－15 6．8‎ ‎7． 8．611‎ ‎9． 10．27‎ ‎11．52‎ ‎12．【解析】因为椭圆上两点、在直线同侧，所以.‎ ‎∵，∴三点共线.‎ ‎（i）当直线斜率不存在时，不妨设，，此时；‎ ‎ ‎ ‎（ii）当直线斜率存在时，设直线方程为：，则有得，由韦达定理得，所以 令，原式 当，原式；‎ 当，原式，等号当且仅当时取得.‎ 二、选择题 ‎13．B 14．B 15．C 16．C 三、解答题 ‎17．（1）证明：取的中点，连接、，∵、分别是、的中点，‎ ‎∴，且，，且，‎ ‎∴，且，则是平行四边形，得，‎ ‎∵平面，平面，∴直线平面；‎ ‎（2）解：连接、，设点到平面的距离为，‎ 由（1）得，点到平面的距离为，‎ 设三棱锥的体积为，则，‎ 依题意，，‎ ‎∵，∴，则.‎ 由，得点到平面的距离.‎ ‎ ‎ ‎18．（1）在中利用正弦定理：‎ 化简得，.‎ 所以停车场面积.‎ 所以..‎ ‎（2）‎ ‎.‎ 所以，当时，停车场面积最大，最大面积约为1039.2平方米.‎ ‎19．（1）由题意，函数在定义域内存在实数，满足，‎ 可得，即，整理得，所以存在满足所以函数是“类函数”.‎ ‎（2）由在上恒成立，可得，‎ 因为为其定义域上的“类函数”，‎ 所以存在实数使得，‎ ‎①当时，则，所以，所以，即，‎ 因为函数，为单调增函数，所以；‎ ‎②当时，，此时，不成立；‎ ‎③当，则，所以，所以 因为函数为单调减函数，所以；‎ ‎ ‎ 综上所述，求实数取值范围.‎ ‎20．（1）根据题意，设椭圆的上下顶点为，，左焦点为，‎ 则是正三角形，所以，则椭圆方程为.‎ 将代入椭圆方程，可得，解得，.故椭圆的方程为.‎ ‎（2）证明：设直线的方程为，，，‎ 由，消去，得 则，且，；‎ 故 ‎.‎ 即直线、、的斜率依次成等比数列.‎ ‎（3）由题意，设直线的方程为，联立，‎ 消去得.‎ 设，，则有，，‎ 因为以线段为直径的圆过椭圆的右顶点，所以，‎ 由，，则，‎ 将，代入上式并整理得，‎ ‎ ‎ 则，化简得，解得或，‎ 因为直线不过点，所以，故.所以直线恒过点.‎ 故设，‎ 则在上单调递增，当时，，所以面积的最大值为.‎ ‎21．（1）由，即对一切恒成立，所以 当时，在上单调递增，所以对任意，均有 综上，实数的取值范围为：；‎ ‎（2）证明：由函数在上单调递减，即对一切，均有 所以对一切，均有，可得：‎ 所以：，对一切，‎ 对任意正实数，取，当时，‎ ‎；‎ ‎（3）非必要性：取，在不为增函数 但，，，，‎ ‎ ‎ 充分性：假设对一切，均有，‎ 所以：（1）‎ 由递推式 因为为增函数，所以（2）‎ 由（1）（2）可知：对一切，均成立 又，可知，当时，上述不等式不成立 所以假设错误，即存在，使得