- 233.50 KB
- 2021-06-03 发布
2018-2019张家港高级中学高二(下)数学(理科)月考试卷
班级_______ 姓名________学号_________
一. 填空题(14*5=70分)
1. 命题“”的否定是_____________________.
2. =____________.
3. 若(),则___________.
4. 已知复数满足,则=___________.
5. 设则_____________.
6. 自点A(-1,4)作圆的切线,则切线长是___________________.
7.用数学归纳法证明()时,从
到,等式左边应增添的项是______________.
8. 已知函数在区间上是减函数,则实数的范围是______.
9. 函数在点处的切线方程是____________.
10. 若定义在区间D上的函数对于D上的个值总满足
,则称函数为D上的凸函数.
现已知在上是凸函数.,在中,则的最大值为_______________.
11. 如果一个三位正整数如“”满足,则称这样的三位数为凸数(如120,343,275等),那么所有的凸数的个数是___________.
12. 已知正整数的三次幂有如下分解规律:,,
若的分解中最小的为111,则的值为_____.
13.设为椭圆 的左、右焦点,经过的直线交椭圆于两点,若 是面积为的等边三角形,则椭圆的方程为 .
14. 0
2 4 8
12 18 24 32 40
50,
大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.通项公式: ,如果把这个数列 排成如图形状,并记 表示第m行中从左
向右第n个数,则 的值为_____________.
二.解答题
15. 已知复数,且为纯虚数. (14分)
(1)求复数;(2)若复数在复平面内对应的点在第二象限,求实数的取值范围.
16. (4+5+5=14分)
(1)求展开式中含的项;
(2)若的展开式中的第4项是常数项,求的值;
(3)若
求
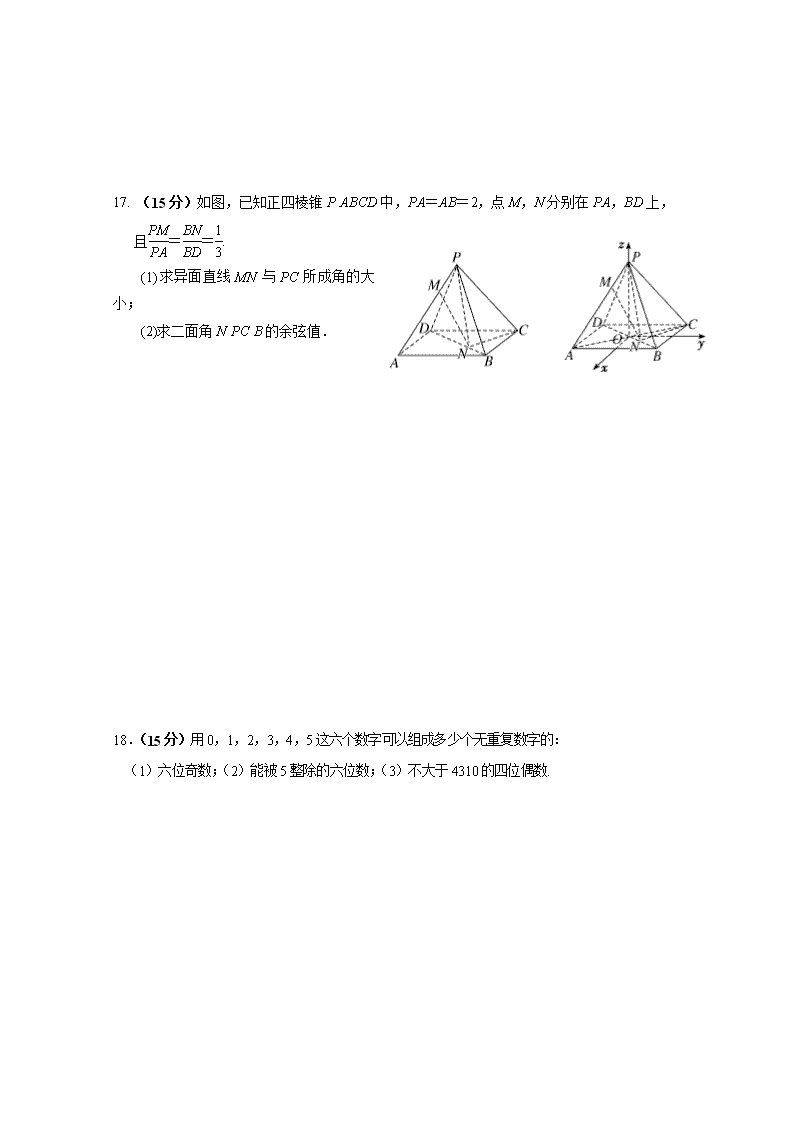
17. (15分)如图,已知正四棱锥PABCD中,PA=AB=2,点M,N分别在PA,BD上,
且==.
(1)求异面直线MN与PC所成角的大小;
(2)求二面角NPCB的余弦值.
18.(15分)用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的:
(1)六位奇数;(2)能被5整除的六位数;(3)不大于4310的四位偶数.
19. (16分)如图,在平面直角坐标系中,已知椭圆的离心率为, 两条准线之间的距离为.
(1)求椭圆的标准方程;(2)已知椭圆的左顶点为A,点M在圆上,直线AM与椭圆相交于另一点B,且的面积是的面积的2倍,求直线AB的方程 .
x
y
A
B
M
O
20. (16分)
已知函数,设为的导函数,
(1)求的表达式;
(2) 求的值;
(3)用数学归纳法证明:
(4)证明:对任意的,等式都成立.