- 932.00 KB
- 2021-06-03 发布
宿迁市2016~2017学年度第一学期高二期末考试
数 学
(考试时间120分钟,试卷满分160分)
参考公式:样本数据的方差,其中.
开始
结束
输出S
Y
N
(第5题)
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1. 写出命题“若,则”的逆命题 ▲ .
Read x
If x<5 Then
y←2x-2
Else
y←x2-2
End If
Print y
(第3题)
2. 抛物线的焦点坐标是 ▲ .
(第4题)
3. 如图所示的伪代码,如果输入x的值为5,则输出的结果y为 ▲ .
4. 如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为,
则阴影部分的面积为 ▲ .
5. 如图是一个算法流程图,则输出的结果为 ▲ .
6.某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在的1000名
学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩
O
y
x
l
3
3
5
(第8题)
y=f(x)
在[120,130)内的学生共有 ▲ 人.
0.015
0.020
100 110 120 130 140 150
0.025
a
0.010
O
成绩(分)
频率/组距
(第6题)
7. 设函数,则函数的单调递增区间是 ▲ .
8. 如图,直线l是曲线在处的切线,表示函数的导函数,
则的值为 ▲ .
x
O
y
B2
A2
B1
A1
(第10题)
9. 已知是圆的一条弦,是弦的中点,
若,则实数的值是 ▲ .
10.如图,椭圆的上、下顶点分别为
,,左、右顶点分别为,,若线段的垂直
平分线恰好经过,则椭圆的离心率是 ▲ .
11.若函数有三个不同的零点,则实数的取值范围是 ▲ .
12.若方程有两个不相等实数根,则实数的取值范围是 ▲ .
13.在平面直角坐标中,已知,,圆上存在唯一的点
满足,则实数的取值集合是 ▲ .
14. 设a>0,函数f(x)=x+,g(x)=x-lnx,若对任意的x2∈[,1],存在,
f(x1)≥g(x2)成立,则实数a的取值范围是 ▲ .
二、解答题: 本大题共6小题, 15—17每小题14分,18—20每小题16分,共计90分.请在答题卡指定的区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用(且)表示.
(1)若乙同学算出自己历史平均成绩是92分,求的值及乙同学历史成绩的方差;
8
9
5 4 3 0
8
6 8
甲
乙
2 8
(第15题)
(2)求甲同学历史平均成绩不低于乙同学历史平均成绩的概率.
16.(本小题满分14分)
已知,.
(1)使成立的实数x的取值集合记为A,成立的实数的取值集合记为B,
当时,求;
(2)若是的充分不必要条件,求实数的取值范围.
17. (本小题满分14分)
已知圆,点.
(1)若线段的中垂线与圆相切,求实数的值;
(2)过直线上的点引圆的两条切线,切点为,若,
则称点为“好点”. 若直线上有且只有两个“好点”,求实数的取值范围.
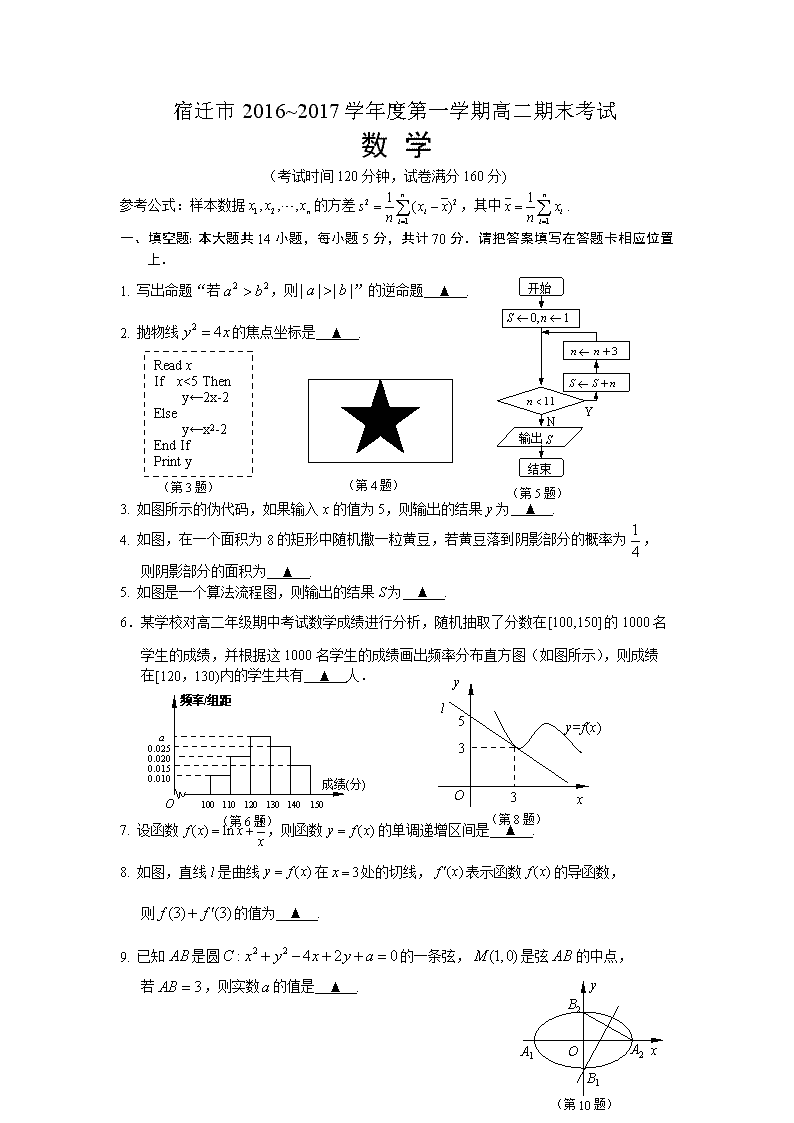
18. (本小题满分16分)
某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为,高为,体积为立方米,且.已知圆柱的侧面部分每平方米建造费用为千元,圆柱的上、下底面部分每平方米建造费用为千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为千元.
(1)求关于的函数表达式,并求出函数的定义域;
h
r
(第18题)
(2)问为多少时,该容器建造总费用最小?
19.(本小题满分16分)
已知椭圆的左、右焦点分别为F1,F2,左、右顶点分别为A1,A2,上、下顶点分别为B2,B1,是斜边长为2的等腰直角三角形,直线l过A2且垂直于x轴,D为l上异于A2的一动点,直线A1D交椭圆于点C.
(1)求椭圆的标准方程;
(2)若A1C=2CD,求直线OD的方程;
(3)求证:为定值.
20.(本小题满分16分)
已知函数,,是两个任意实数且.
(1)求函数的图象在处的切线方程;
(2)若函数在上是增函数,求的取值范围;
(3)求证:.
数学参考答案与评分标准
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.若,则; 2. ; 3. 23; 4. 2; 5. 22;
6.300; 7. ; 8. ; 9. ; 10. ;
11. ; 12. ; 13. ; 14. ;
二、解答题: 本大题共6小题, 15—17每小题14分,18—20每小题16分,共计90分.请在答题卡指定的区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(1)因为乙同学历史平均成绩是92分,所以,
解得. ……………………3分
此时乙同学的历史成绩的方差为
=;………6分
(2)甲同学的历史平均成绩为分, …………………8分
若甲的历史平均成绩不低于乙同学历史平均成绩,
则,得. ……………………10分
因为,所以且,
记甲同学历史平均成绩不低于乙同学历史平均成绩为事件,
则事件包含4个基本事件,而基本事件总数共有6个,
所以事件的概率. ……………………13分
答:(1)的值为6,乙同学历史成绩的方差为;
(2)甲同学历史平均成绩不低于乙同学历史平均成绩的概率为.……14分
16.(1)因为,所以,则A;……………2分
因为,所以,
所以, ……………4分
当时,, ……………6分
所以. ……………7分
(2)因为是的充分不必要条件,所以且, ……………10分
则, ……………12分
解得,
所以当时,是的必要不充分条件. ……………14分
17.(1)由得的中点坐标为,直线的斜率为,……..2分
所以的中垂线方程为,即, …………..4分
又因为的中垂线与圆相切,
所以圆心到中垂线的距离,即. ……………………6分
(2)连接,
在中,,
所以,……………………………………………………….8分
所以点的轨迹是以为圆心,为半径的圆,记为圆,
则圆的方程为,……………………………………………..10分
又因为直线的方程为,且直线上有且只有两个“好点”,
则直线与圆相交,所以圆心到直线的距离,
故实数的取值范围是. …………………….14分
18.(1)设容器的容积为,
由题意知,故,………………………………..2分
因为,所以,……………………………………………….4分
故建造费用,
即. ………………………………………….6分
(2)由(1)得,
令得, ……..8分
①当即时,
若,则,函数单调递减;
若,则,函数单调递增;
所以时,函数取得极小值,也是最小值. ……………….....12分
②当即时,
因为,则,函数单调递减;
则时,函数取得最小值. ………………………………………...14分
综上所述: 若,当时,建造总费用最少;
若,当时,建造总费用最少. ………………..16分
19.(1)因为是斜边长为2的等腰直角三角形,
所以,
又因为,所以,
所以椭圆标准方程为. ………4分
(2)设,,
因为AC=2CD,所以,
所以有, ……………6分
所以,解得,代入椭圆方程得,
则当时,,,直线OD的方程为y=x; ……………8分
当 时,,直线OD的方程为.……………10分
(3)(解法一)设,
则直线A1D: ,即,
代入椭圆得
. ………………………12分
因为,所以,,
则, …………………………14分
所以(定值). …16分
(解法二)由已知直线A1D斜率存在,设A1D的方程为,
设由得,
即, ……12分
则,,,
则,
故. ………………14分
由令x=2,得y=4k,则,故
所以,=(定值)………………16分
20.(1)因为, ………………1分
则切线的斜率为,切点为,
所以函数的图象在处切线方程为; ……………3分
(2)由得,
因为函数在实数集上是增函数,
所以恒成立, ………………5分
则恒成立,
令,
由得, ………………7分
当时,,函数递减;
当时,,函数递增;
所以当时,函数,
故实数的取值范围是. ………………9分
(3)要证明,即证明,
只需证明,不妨设,,
只需证明(),
只需证明对恒成立, ………………11分
设,
则,
设,当时恒成立,
则递增,,即, ………………13分
则,故函数递增,有恒成立,
即对恒成立,
所以,即. ………………16分