- 578.00 KB
- 2021-06-03 发布
2016-2017学年河北省唐山一中高二(上)期中数学试卷(文科)
一.选择题(共12小题,每小题5分,计60分.在每小题给出的四个选项中只有一个选项正确)
1.双曲线3x2﹣y2=9的实轴长是( )
A.2 B.2 C.4 D.4
2.抛物线y=﹣x2的准线方程是( )
A. B.y=2 C. D.y=﹣2
3.已知直线l过圆x2+(y﹣3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是( )
A.x+y﹣2=0 B.x﹣y+2=0 C.x+y﹣3=0 D.x﹣y+3=0
4.已知椭圆,长轴在y轴上,若焦距为4,则m等于( )
A.4 B.5 C.7 D.8
5.若△ABC的个顶点坐标A(﹣4,0)、B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
A. B.(y≠0)
C.(y≠0) D.(y≠0)
6.直线y=kx﹣k+1与椭圆的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
7.已知圆(x﹣a)2+y2=4截直线y=x﹣4所得的弦的长度为2,则a等于( )
A.2 B.6 C.2或6 D.
8.在正方体AC1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是( )
A.相交 B.异面 C.平行 D.垂直
9.已知双曲线(a>0,b>0)的两条渐近线均和圆C:x2+y2﹣6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=1
10.四棱锥P﹣ABCD的所有侧棱长都为,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )
A. B. C. D.
11.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的最大值为( )
A.7 B.6 C.5 D.4
12.已知F是椭圆C: +=1(a>b>0)的右焦点,点P在椭圆C上,且线段PF与圆(其中c2=a2﹣b2)相切于点Q,且=2,则椭圆C的离心率等于( )
A. B. C. D.
二.填空题(共4小题,每小题5分,计20分)
13.已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 .
14.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长是10 cm,则圆锥的母线长为 cm.
15.已知双曲线x2﹣y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为 .
16.如图是某几何体的三视图,则该几何体的外接球的表面积 .
三.计算题(共6小题,第17题10分,第18-22题每题12分,共计70分,解答题应写出必要的文字说明,证明过程或演算步骤)
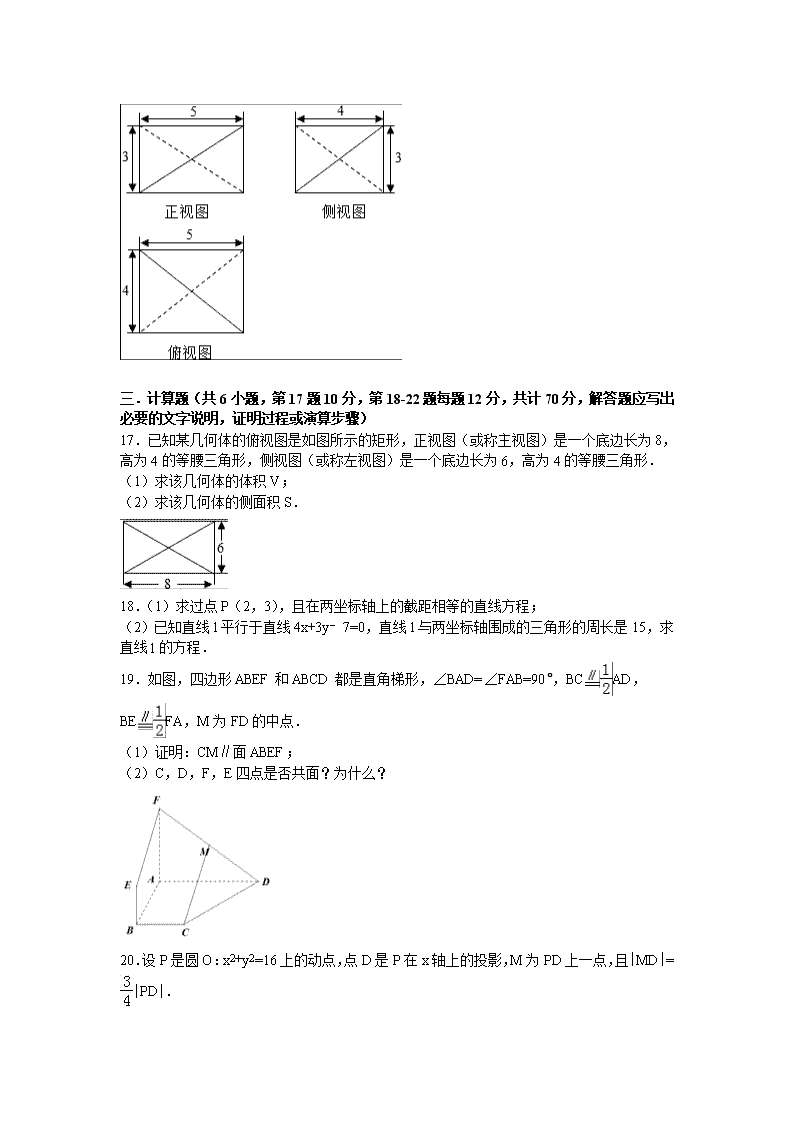
17.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
18.(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程;
(2)已知直线l平行于直线4x+3y﹣7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
19.如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BCAD,BEFA,M为FD的中点.
(1)证明:CM∥面ABEF;
(2)C,D,F,E四点是否共面?为什么?
20.设P是圆O:x2+y2=16上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=|PD|.
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(2,0)且斜率为的直线被C所截线段的长度.
21.已知过抛物线y2=2px(p>0)的焦点,斜率为的直线交抛物线于A(x1,y1)和B(x2,y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若,求λ的值.
22.已知圆O:x2+y2=9及点C(2,1).
(1)若线段OC的垂直平分线交圆O于A,B两点,试判断四边形OACB的形状,并给予证明;
(2)过点C的直线l与圆O交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
2016-2017学年河北省唐山一中高二(上)期中数学试卷(文科)
参考答案与试题解析
一.选择题(共12小题,每小题5分,计60分.在每小题给出的四个选项中只有一个选项正确)
1.双曲线3x2﹣y2=9的实轴长是( )
A.2 B.2 C.4 D.4
【考点】双曲线的简单性质.
【分析】求出双曲线的标准方程进行求解即可.
【解答】解:双曲线的标准方程为﹣=1,
则a2=3,则a=,
即双曲线3x2﹣y2=9的实轴长2a=2,
故选:A.
2.抛物线y=﹣x2的准线方程是( )
A. B.y=2 C. D.y=﹣2
【考点】抛物线的简单性质.
【分析】先把抛物线转换为标准方程x2=﹣8y,然后再求其准线方程.
【解答】解:∵,
∴x2=﹣8y,
∴其准线方程是y=2.
故选B.
3.已知直线l过圆x2+(y﹣3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是( )
A.x+y﹣2=0 B.x﹣y+2=0 C.x+y﹣3=0 D.x﹣y+3=0
【考点】直线与圆的位置关系.
【分析】由题意可得所求直线l经过点(0,3),斜率为1,再利用点斜式求直线l的方程.
【解答】解:由题意可得所求直线l经过点(0,3),斜率为1,
故l的方程是 y﹣3=x﹣0,即x﹣y+3=0,
故选:D.
4.已知椭圆,长轴在y轴上,若焦距为4,则m等于( )
A.4 B.5 C.7 D.8
【考点】椭圆的简单性质.
【分析】先把椭圆方程转换成标准方程,进而根据焦距求得m.
【解答】解:将椭圆的方程转化为标准形式为,
显然m﹣2>10﹣m,即m>6,
,解得m=8
故选D
5.若△ABC的个顶点坐标A(﹣4,0)、B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
A. B.(y≠0)
C.(y≠0) D.(y≠0)
【考点】与直线有关的动点轨迹方程;椭圆的标准方程.
【分析】由△ABC的个顶点坐标A(﹣4,0)、B(4,0),△ABC的周长为18,得顶点C到A、B的距离和为定值10>8,由椭圆定义可知,顶点C的轨迹为椭圆,且求得椭圆的长轴长及焦距,则答案可求.
【解答】解:∵A(﹣4,0)、B(4,0),∴|AB|=8,
又△ABC的周长为18,∴|BC|+|AC|=10.
∴顶点C的轨迹是一个以A、B为焦点的椭圆,
则a=5,c=4,b2=a2﹣c2=25﹣16=9,
∴顶点C的轨迹方程为.
故选:D.
6.直线y=kx﹣k+1与椭圆的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
【考点】直线与圆锥曲线的关系.
【分析】直线y=kx﹣k+1恒过点(1,1),且在椭圆的内部,由此可得直线y=kx﹣k+1与椭圆的位置关系.
【解答】解:直线y=kx﹣k+1可化为y=k(x﹣1)+1,所以直线恒过点(1,1)
∵
∴(1,1)在椭圆的内部
∴直线y=kx﹣k+1与椭圆的位置关系是相交
故选A.
7.已知圆(x﹣a)2+y2=4截直线y=x﹣4所得的弦的长度为2,则a等于( )
A.2 B.6 C.2或6 D.
【考点】直线与圆的位置关系.
【分析】先求出圆心(a,0)到直线y=x﹣4的距离d=,再由勾股定理能求出a.
【解答】解:∵圆(x﹣a)2+y2=4截直线y=x﹣4所得的弦的长度为2,
圆心(a,0)到直线y=x﹣4的距离d=,
∴=,
解得a=2或a=6.
故选C.
8.在正方体AC1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是( )
A.相交 B.异面 C.平行 D.垂直
【考点】空间中直线与直线之间的位置关系.
【分析】直线AB与直线外一点E确定的平面为A1BCD1,EF⊂平面A1BCD1,且两直线不平行,故两直线相交,可得结论.
【解答】解:如图,在正方体AC1中:
∵A1B∥D1C
∴A1B与D1C可以确定平面A1BCD1,
又∵EF⊂平面A1BCD1,且两直线不平行,
∴直线A1B与直线EF的位置关系是相交,
故选A.
9.已知双曲线(a>0,b>0)的两条渐近线均和圆C:x2+y2﹣6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=1
【考点】双曲线的简单性质;双曲线的标准方程.
【分析】先利用圆的一般方程,求得圆心坐标和半径,从而确定双曲线的焦距,得a、b间的一个等式,再利用直线与圆相切的几何性质,利用圆心到渐近线距离等于圆的半径,得a、b间的另一个等式,联立即可解得a、b的值,从而确定双曲线方程
【解答】解:∵圆C:x2+y2﹣6x+5=0的圆心C(3,0),半径r=2
∴双曲线(a>0,b>0)的右焦点坐标为(3,0),即c=3,∴a2+b2=9,①
∵双曲线(a>0,b>0)的一条渐近线方程为bx﹣ay=0,
∴C到渐近线的距离等于半径,即=2 ②
由①②解得:a2=5,b2=4
∴该双曲线的方程为
故选 A
10.四棱锥P﹣ABCD的所有侧棱长都为,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )
A. B. C. D.
【考点】余弦定理的应用;异面直线及其所成的角.
【分析】根据CD∥AB,∠PAB或其补角就是异面直线CD与PA所成的角,在△PAB中求出∠PAB的余弦值,即可得出CD与PA所成角的余弦值.
【解答】解:∵正方形ABCD中,CD∥AB
∴∠PAB或其补角就是异面直线CD与PA所成的角
△PAB中,PA=PB=,AB=2
∴cos∠PAB===
即CD与PA所成角的余弦值为
故选A
11.已知圆C:(x﹣3)2+(y﹣4)2=1和两点A(﹣m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的最大值为( )
A.7 B.6 C.5 D.4
【考点】直线与圆的位置关系.
【分析】根据圆心C到O(0,0)的距离为5,可得圆C上的点到点O的距离的最大值为6.再由∠APB=90°,可得PO=AB=m,可得m≤6,从而得到答案.
【解答】解:圆C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径为1,
∵圆心C到O(0,0)的距离为5,
∴圆C上的点到点O的距离的最大值为6.
再由∠APB=90°可得,以AB为直径的圆和圆C有交点,
可得PO=AB=m,故有m≤6,
故选:B.
12.已知F是椭圆C: +=1(a>b>0)的右焦点,点P在椭圆C上,且线段PF与圆(其中c2=a2﹣b2)相切于点Q,且=2,则椭圆C的离心率等于( )
A. B. C. D.
【考点】椭圆的简单性质;直线与圆的位置关系.
【分析】设椭圆的左焦点为F1,确定PF1⊥PF,|PF1|=b,|PF|=2a﹣b,即可求得椭圆的离心率.
【解答】解:设椭圆的左焦点为F1,连接F1,设圆心为C,则
∵
∴圆心坐标为,半径为r=
∴|F1F|=3|FC|
∵=2,
∴PF1∥QC,|PF1|=b
∴|PF|=2a﹣b
∵线段PF与圆(其中c2=a2﹣b2)相切于点Q,
∴CQ⊥PF
∴PF1⊥PF
∴b2+(2a﹣b)2=4c2
∴b2+(2a﹣b)2=4(a2﹣b2)
∴
∴
∴
故选A.
二.填空题(共4小题,每小题5分,计20分)
13.已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 4 .
【考点】椭圆的简单性质.
【分析】设另一个焦点为F,根据椭圆的定义可知|AB|+|BF|=2a,|AC|+|FC|=2a最后把这四段线段相加求得△ABC的周长.
【解答】解:椭圆+y2=1的a=.
设另一个焦点为F,则根据椭圆的定义可知
|AB|+|BF|=2a=2,|AC|+|FC|=2a=2.
∴三角形的周长为:|AB|+|BF|+|AC|+|FC|=4.
故答案为:4.
14.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长是10 cm,则圆锥的母线长为 13 cm.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】作出圆锥的轴截面如图,利用平行线截线段成比例,求出SA′,求出圆锥的母线长.
【解答】解:作出圆锥的轴截面如图,设SA=y,O′A′=x;
利用平行线截线段成比例,
则SA′:SA=O′A′:OA,即(y﹣10):y=x:4x,
解得y=13.
即圆锥的母线长为13cm.
故答案为:13
15.已知双曲线x2﹣y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为 .
【考点】双曲线的简单性质.
【分析】根据双曲线方程为x2﹣y2=1,可得焦距F1F2=2,因为PF1⊥PF2,所以|PF1|2+|PF2|2=|F1F2|2.再结合双曲线的定义,得到|PF1|﹣|PF2|=±2,最后联解、配方,可得(|PF1|+|PF2|)2=12,从而得到|PF1|+|PF2|的值为.
【解答】解:∵PF1⊥PF2,
∴|PF1|2+|PF2|2=|F1F2|2.
∵双曲线方程为x2﹣y2=1,
∴a2=b2=1,c2=a2+b2=2,可得F1F2=2
∴|PF1|2+|PF2|2=|F1F2|2=8
又∵P为双曲线x2﹣y2=1上一点,
∴|PF1|﹣|PF2|=±2a=±2,(|PF1|﹣|PF2|)2=4
因此(|PF1|+|PF2|)2=2(|PF1|2+|PF2|2)﹣(|PF1|﹣|PF2|)2=12
∴|PF1|+|PF2|的值为
故答案为:
16.如图是某几何体的三视图,则该几何体的外接球的表面积 50π .
【考点】由三视图求面积、体积.
【分析】根据几何体的三视图,得出该几何体是长方体内的三棱锥,结合图形,求出该三棱锥的外接球的半径即可.
【解答】解:根据几何体的三视图,得;
该几何体是顶点与长方体的顶点重合的三棱锥B1﹣ACD1,如图所示,
长方体的长为5,宽为4,高为3,
∴该三棱锥的外接球即为长方体的外接球,该球的直径为2R=l,
∴l2=52+42+32=50,
∴外接球的表面积是S球=4πR2=πl2=50π.
故答案为:50π.
三.计算题(共6小题,第17题10分,第18-22题每题12分,共计70分,解答题应写出必要的文字说明,证明过程或演算步骤)
17.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
【考点】由三视图求面积、体积.
【分析】由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,分析出图形之后,再利用公式求解即可.
【解答】解:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,如图所示.
(1)几何体的体积为
V=•S矩形•h=×6×8×4=64.
(2)正侧面及相对侧面底边上的高为:
h1==5.
左、右侧面的底边上的高为:
h2==4.
故几何体的侧面面积为:
S=2×(×8×5+×6×4)
=40+24.
18.(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程;
(2)已知直线l平行于直线4x+3y﹣7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
【考点】直线的截距式方程.
【分析】(1)根据直线的截距关系即可求出直线方程;
(2)利用直线平行的关系,结合三角形的周长即可得到结论.
【解答】解:(1)当直线过原点时,过点(2,3)的直线为
当直线不过原点时,设直线方程为(a≠0),直线过点(2,3),
代入解得a=5
∴直线方程为
∴过P(2,3),且在两坐标轴上的截距相等的直线方程为3x﹣2y=0和x+y﹣5=0.
(2)∵直线l与直线4x+3y﹣7=0平行,∴.
设直线l的方程为,
则直线l与x轴的交点为A,与y轴的交点为B(0,b),
∴.
∵直线l与两坐标轴围成的三角形周长是15,
∴.
∴|b|=5,∴b=±5.
∴直线l的方程是,
即4x+3y±15=0.
19.如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BCAD,BEFA,M为FD的中点.
(1)证明:CM∥面ABEF;
(2)C,D,F,E四点是否共面?为什么?
【考点】平面的基本性质及推论;直线与平面平行的判定.
【分析】(1)设G为AF的中点,连接BG,GM,CM,推导出四边形BCMG为平行四边形,从而CM∥BG,由此能证明CM∥平面ABEF.
(2)推导出四边形BEFG为平行四边形,从而EF∥BG,进而EF∥CM,由此得到C,D,F,E四点共面.
【解答】证明:(1)设G为AF的中点,连接BG,GM,CM,
由已知FG=GA,FM=MD,可得GMAD,BCAD,
∴GMBC,
∴四边形BCMG为平行四边形,∴CM∥BG,
∵BG⊂ABEF,CM⊄面ABEF,
∴CM∥平面ABEF.
解:(2)由BEFA,G为FA中点知,BEFG,
∴四边形BEFG为平行四边形,∴EF∥BG,
由(1)知BGCM,∴EF∥CM,∴EF与CM共面.
又D∈FM,∴C,D,F,E四点共面.
20.设P是圆O:x2+y2=16上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=|PD|.
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(2,0)且斜率为的直线被C所截线段的长度.
【考点】直线与圆的位置关系.
【分析】(1)设M的坐标为(x,y),P的坐标为(xP,yP),由已知得xP=x,yP=y,由此能求出C的方程.
(2)过点(2,0)且斜率为的直线方程为y=(x﹣2),与=1联立可得x2﹣2x﹣6=0,即可求出过点(2,0)且斜率为的直线被C所截线段的长度.
【解答】解:(1)设M的坐标为(x,y),P的坐标为(xP,yP),
∵P是圆x2+y2=16上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=|PD|,
∴xP=x,yP=y,
∵P在圆上,∴x2+y2=16,即C的方程为=1;
(2)过点(2,0)且斜率为的直线方程为y=(x﹣2),与=1联立可得x2﹣2x﹣6=0
∴过点(2,0)且斜率为的直线被C所截线段的长度==.
21.已知过抛物线y2=2px(p>0)的焦点,斜率为的直线交抛物线于A(x1,y1)和B(x2,y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若,求λ的值.
【考点】抛物线的标准方程;直线与圆锥曲线的综合问题.
【分析】(1)直线AB的方程与y2=2px联立,有4x2﹣5px+p2=0,从而x1+x2=,再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.
(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2),B(4,4).再求得设的坐标,最后代入抛物线方程即可解得λ.
【解答】解:(1)直线AB的方程是y=2(x﹣),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2=
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x.
(2)由p=4,4x2﹣5px+p2=0得:x2﹣5x+4=0,
∴x1=1,x2=4,
y1=﹣2,y2=4,从而A(1,﹣2),B(4,4).
设=(x3,y3)=(1,﹣2)+λ(4,4)=(4λ+1,4λ﹣2)
又[2(2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2.
22.已知圆O:x2+y2=9及点C(2,1).
(1)若线段OC的垂直平分线交圆O于A,B两点,试判断四边形OACB的形状,并给予证明;
(2)过点C的直线l与圆O交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
【考点】直线与圆的位置关系.
【分析】(1)OC的中点为(1,),设OC的垂直平分线为y=﹣2x+,代入圆x2+y2=9,得=0,由韦达定理及中点坐标公式得到AB的中点为(1,),再由OC⊥AB,推导出四边形OACB为菱形.
(2)当直线l的斜率不存在时,S△OPQ=2,当直线l的斜率存在时,设l的方程为y﹣1=k(x﹣2),(k),圆心到直线PQ的距离为d=,由平面几何知识得|PQ|=2,推导出当且仅当d2=时,S△OPQ取得最大值,由此能求出直线l的方程.
【解答】解:(1)四边形OACB为菱形,证明如下:
OC的中点为(1,),设A(x1,y1),B(,y2),
设OC的垂直平分线为y=﹣2x+,代入圆x2+y2=9,得=0,
∴, =﹣2×=,
∴AB的中点为(1,),
∴四边形OACB为平行四边形,
又OC⊥AB,∴四边形OACB为菱形.
(2)当直线l的斜率不存在时,l的方程为x=2,则P、Q的坐标为(2,),(2,﹣),
∴S△OPQ==2,
当直线l的斜率存在时,设l的方程为y﹣1=k(x﹣2),(k),
则圆心到直线PQ的距离为d=,
由平面几何知识得|PQ|=2,
∴S△OPQ==d=≤=,
当且仅当9﹣d2=d2,即d2=时,S△OPQ取得最大值,
∵,∴S△OPQ的最大值为,
此时,由=,解得k=﹣7或k=﹣1.
此时,直线l的方程为x+y﹣3=0或7x+y﹣15=0.