- 226.50 KB
- 2021-06-03 发布
2017年高考全真模拟试题(一)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试时间120分钟,满分150分.
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|y=},B={x|-1≤2x-1≤0},则(∁RA)∩B=( )
A.(4,+∞) B.
C. D.(1,4]
答案 B
解析 由题意得,A=[4,+∞),B=,∴(∁RA)∩B=,故选B.
2.设复数z1=2-i,z2=a+2i(i是虚数单位,a∈R),若z1·z2∈R,则a等于( )
A.1 B.-1
C.4 D.-4
答案 C
解析 依题意,复数z1z2=(2-i)(a+2i)=(2a+2)+(4-a)i是实数,因此4-a=0,a=4,选C.
3.已知命题p:若a0,使得x0-1-ln x0=0,则下列命题为真命题的是( )
A.p∧q B.p∨(綈q)
C.(綈p)∧q D.(綈p)∧(綈q)
答案 C
解析 依题意,对于p,注意到当c=0时,ac2=bc2,因此命题
p是假命题;对于q,注意到当x0=1时,x0-1-ln x0=0,因此命题q是真命题,命题綈p是真命题,p∧q是假命题,p∨(綈q)是假命题,(綈p)∧q是真命题,(綈p)∧(綈q)是假命题.综上所述,选C.
4.[2016·石家庄二模]投掷两枚骰子,则点数之和是8的概率为( )
A. B.
C. D.
答案 A
解析 投掷两枚骰子,点数形成的事件共有6×6=36种,其中点数之和为8的事件有(2,6),(3,5),(4,4),(5,3),(6,2)共5种,因此所求概率为P=.
5.设Sn为等比数列{an}的前n项和,a2-8a5=0,则的值为( )
A. B.
C.2 D.17
答案 B
解析 设{an}的公比为q,依题意得==q3,因此q=.注意到a5+a6+a7+a8=q4(a1+a2+a3+a4),即有S8-S4=q4S4,因此S8=(q4+1)S4,=q4+1=,选B.
6.过抛物线y2=4x的焦点的直线l交抛物线于P(x1,y1),Q(x2,y2)两点,如果x1+x2=6,则|PQ|=( )
A.9 B.8
C.7 D.6
答案 B
解析 抛物线y2=4x的焦点为F(1,0),准线方程为x
=-1.根据题意可得,|PQ|=|PF|+|QF|=x1+1+x2+1=x1+x2+2=8.故选B.
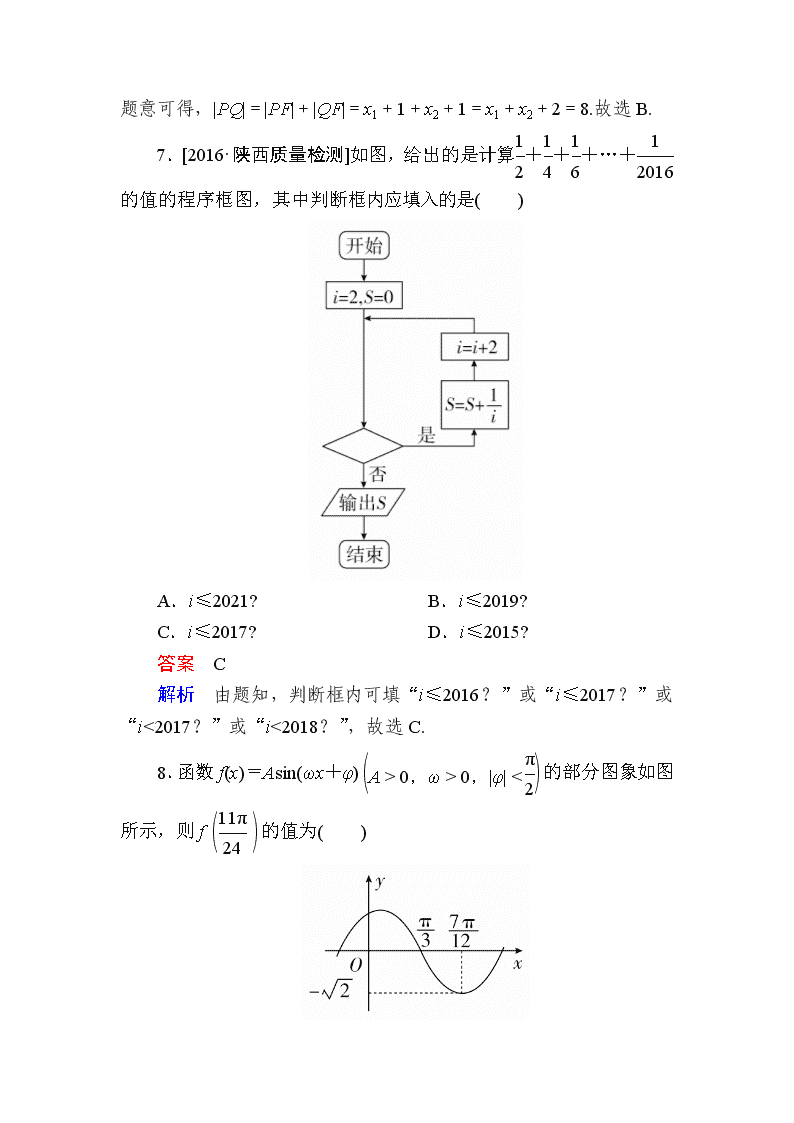
7.[2016·陕西质量检测]如图,给出的是计算+++…+的值的程序框图,其中判断框内应填入的是( )
A.i≤2021? B.i≤2019?
C.i≤2017? D.i≤2015?
答案 C
解析 由题知,判断框内可填“i≤2016?”或“i≤2017?”或“i<2017?”或“i<2018?”,故选C.
8.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f的值为( )
A.- B.-
C.- D.-1
答案 D
解析 由图象可得A=,最小正周期T=4×=π,则ω==2.又f=sin=-,得φ=,则f(x)=sin,f=sin=sin=-1,选项D正确.
9.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
A.π B.
C.3π D.3
答案 A
解析 由题意得,该几何体为四棱锥,且该四棱锥的外接球即为棱长为1的正方体的外接球,其半径为,故体积为π3=π,故选A.
10.设实数x,y满足约束条件则x2+(y+2)2的取值范围是( )
A. B.[1,17]
C.[1,] D.
答案 A
解析 画出可行域如图阴影部分所示,设x2+(y+2)2=r2,当圆过点A(-1,2)时,r2取得最大值为(-1)2+(2+2)2=1+16=17;当圆与直线x-y-1=0相切时,r取得最小值为=,则r2=,∴x2+(y+2)2的取值范围是.
11.已知点F1、F2分别是双曲线C:-=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线C的左、右两支分别交于A、B两点,若|AB|∶|BF2|∶|AF2|=3∶4∶5,则双曲线的离心率为( )
A.2 B.4
C. D.
答案 C
解析 由题意,设|AB|=3k,|BF2|=4k,|AF2|=5k,则BF1⊥BF2,|AF1|=|AF2|-2a=5k-2a,又|BF1|-|BF2|=5k-2a+3k-4k=4k-2a=2a,∴a=k,∴|BF1|=6a,|BF2|=4a,又|BF1|2+|BF2|2=|F1F2|2,即13a2=c2,∴e==,故选C.
12.已知定义在R上的奇函数y=f(x)的图象关于直线x=1对称,当-1≤x<0时,f(x)=-log (-x),则方程f(x)-=0在(0,6)内的所有根之和为( )
A.8 B.10
C.12 D.16
答案 C
解析 ∵奇函数f(x)的图象关于直线x=1对称,
∴f(x)=f(2-x)=-f(-x),即f(x)=-f(x+2)=f(x+4),
∴f(x)是周期函数,其周期T=4.又当x∈[-1,0)时,f(x)=-log (-x),故f(x)在(0,6)上的函数图象如图所示.
由图可知方程f(x)-=0在(0,6)内的根共有4个,其和为x1+x2+x3+x4=2+10=12,故选C.
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.
二、填空题(本大题共4小题,每小题5分)
13.已知在(-1,1)上函数f(x)=且f(x)=-,则x的值为________.
答案 -
解析 解法一:当-110.828.
所以至少有99.9%的把握认为疫苗有效.
19.(本小题满分12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=BC=2,AB=2,求三棱锥C-A1DE的体积.
解 (1)证明:连接AC1交A1C于点F,则F为AC1中点.
又D是AB中点,连接DF,
则BC1∥DF.
因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.
(2)因为ABC-A1B1C1是直三棱柱,
所以AA1⊥CD.
由已知AC=CB,D为AB的中点,
所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2得
∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以V三棱锥C-A1DE=××××=1.
20.(本小题满分12分)已知椭圆E:+=1(a>b>0)经过点(2,2),且离心率为,F1,F2是椭圆E的左,右焦点.
(1)求椭圆E的方程;
(2)若点A,B是椭圆E上关于y轴对称的两点(A,B不是长轴的端点),点P是椭圆E上异于A,B的一点,且直线PA,PB分别交y轴于点M,N,求证:直线MF1与直线NF2的交点G在定圆上.
解 (1)由条件得a=4,b=c=2,
故椭圆E的方程为+=1.
(2)证明:设B(x0,y0),P(x1,y1),则A(-x0,y0).
直线PA的方程为y-y1=(x-x1),
令x=0,得y=,
故M.同理可得N.
所以=,
=,
所以·=·
=-8+=-8+
=-8+8=0,
所以F1M⊥F2N,所以直线MF1与直线NF2的交点G在以F1F2为直径的圆上.
21.(本小题满分12分)已知函数f(x)=x3-mx在点(1,f(1))处的切线与y轴垂直.
(1)判断函数f(x)的单调性;
(2)设函数g(x)=ex-ex(e为自然对数的底数),如果对任意的x1,x2∈,都有f(x1)-g(x2)≤3n2+n恒成立,求实数n的取值范围.
解 (1)因为f(x)=x3-mx,所以f′(x)=3x2-m.
因为函数f(x)=x3-mx在点(1,f(1))处的切线与y轴垂直,
所以f′(1)=0,
所以3-m=0,解得m=3.
所以f′(x)=3x2-3=3(x+1)(x-1).
当x<-1或x>1时,f′(x)>0;
当-11时,g′(x)>0;
所以g(x)在上单调递减,在(1,2]上单调递增,
故函数g(x)在上的最小值g(x)min=g(1)=0.
所以3n2+n≥2,解得n≤-1或n≥,
故实数n的取值范围是(-∞,-1]∪.
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
已知平面直角坐标系xOy,直线l的参数方程为,若以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ+2cosθ=0.
(1)写出直线l和曲线C的直角坐标方程;
(2)若直线l与曲线C相切,求tanα的值.
解 (1)由消去参数t得y=tanα·(x-1),
所以直线l的直角坐标方程为y=tanα·(x-1).
由ρsin2θ+2cosθ=0,得ρ2sin2θ+2ρcosθ=0,
将代入,解得曲线C的直角坐标方程y2=-2x.
(2)由(1),联立方程组
化简得tan2α·x2+2(1-tan2α)x+tan2α=0,
则由Δ=4(1-tan2α)2-4tan4α=0,
解得tanα=±.
23.(本小题满分10分)选修4-5:不等式选讲
已知二次函数f(x)=ax2+bx+c(a≠0).
(1)若函数y=f(x)的图象过原点,且|f(x)|≤1的解集为{x|-1≤x≤3},求f(x)的解析式;
(2)若x=-1,0,1时的函数值的绝对值均不大于1,当x∈[-1,1]时,求证:|ax+b|≤2.
解 (1)由函数f(x)的图象过原点,得c=0,
所以|f(x)|≤1可化为|ax2+bx|≤1,其解集为{x|-1≤x≤3},则由数形结合得|ax2+bx|=1的解为x=-1或x=3,且≤1,
解得a=-,b=或a=,b=-,
所以f(x)=-x2+x或f(x)=x2-x.
(2)证明:由题意知
若证x∈[-1,1]时,|ax+b|≤2,
则只需证|a+b|≤2且|a-b|≤2,
因为|a+b|=|(a+b+c)-c|≤|a+b+c|+|c|≤2,
|a-b|=|(a-b+c)-c|≤|a-b+c|+|c|≤2,
所以|ax+b|≤2.