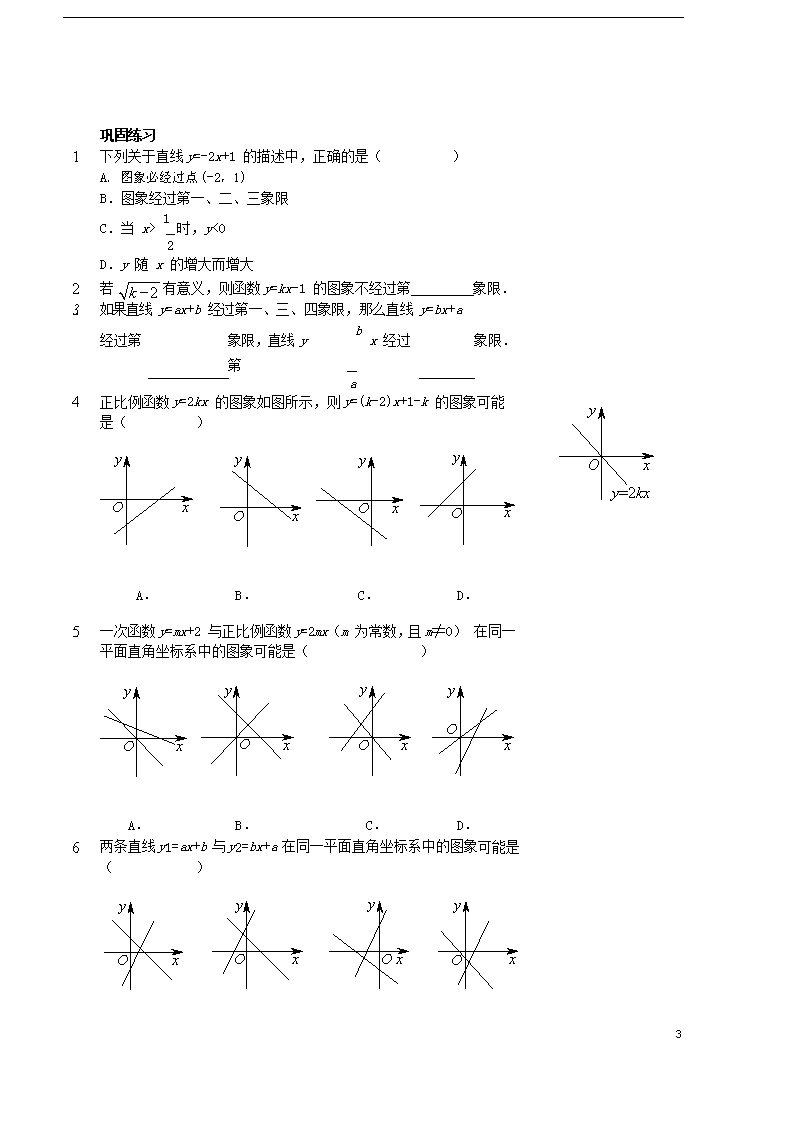- 237.00 KB
- 2021-06-03 发布
一次函数图象的应用(习题)
Ø 例题示范
例 1:已知一次函数 y=kx+b 与正比例函数 y=kbx,它们在同一平面直角坐标系中的图象可能是( )
y
O
x
y
O
x
y
O
x
y
O
x
A. B. C. D.
思路分析: 选项 A:
假设一次函数 y=kx+b 图象正确,则 k<0,b>0,
∴kb<0,由图象知,正比例函数可以与之共存,选项 A 正确; 选项 B:
假设一次函数 y=kx+b 图象正确,则 k<0,b>0,
∴kb<0,由图象知,正比例函数不能与之共存,选项 B 错误; 选项 C:
假设一次函数 y=kx+b 图象正确,则 k>0,b<0,
∴kb<0,由图象知,正比例函数不能与之共存,选项 C 错误; 选项 D:
假设一次函数 y=kx+b 图象正确,则 k>0,b>0,
∴kb>0,由图象知,正比例函数不能与之共存,选项 D 错误. 故选 A.
8
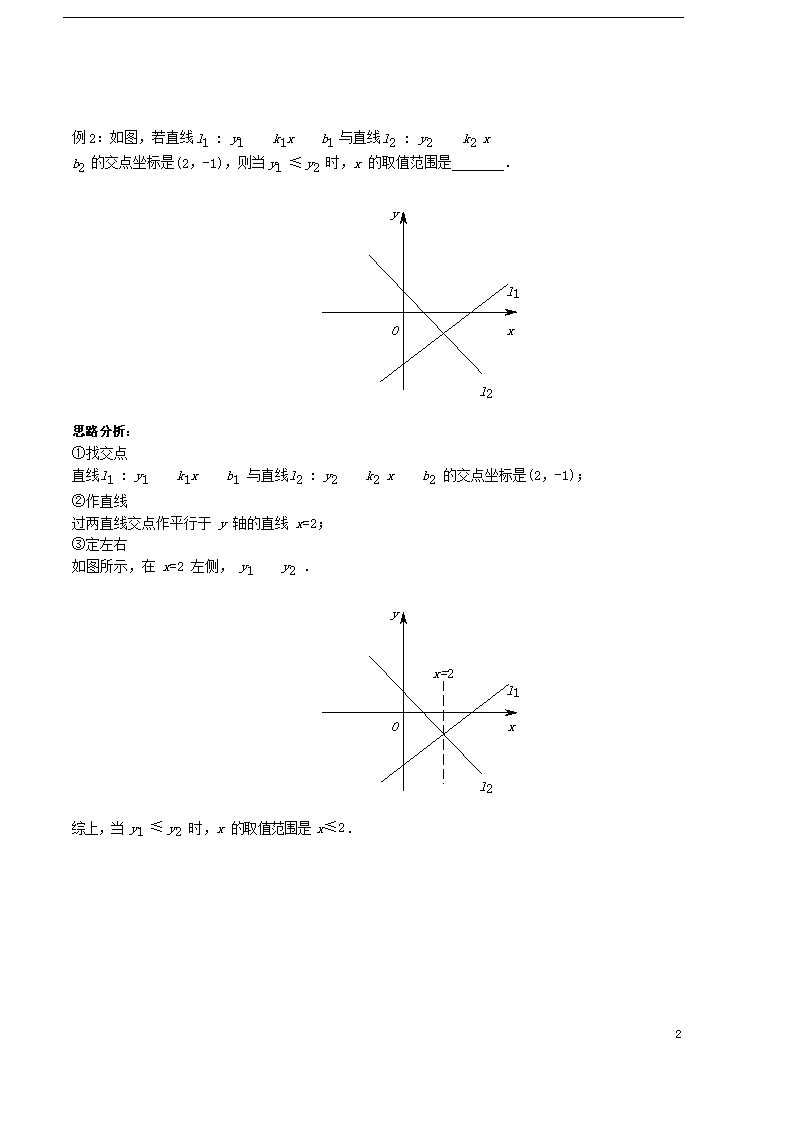
例 2:如图,若直线l1 : y1 = k1x + b1 与直线l2 : y2 = k2 x + b2 的交点坐标是(2,-1),则当 y1 ≤ y2 时,x 的取值范围是 .
y
l1
O x
l2
思路分析:
①找交点
直线l1 : y1 = k1x + b1 与直线l2 : y2 = k2 x + b2 的交点坐标是(2,-1);
②作直线
过两直线交点作平行于 y 轴的直线 x=2;
③定左右
如图所示,在 x=2 左侧, y1 < y2 .
y
x=2
l1
O x
l2
综上,当 y1 ≤ y2 时,x 的取值范围是 x≤2.
8
Ø 巩固练习
1. 下列关于直线 y=-2x+1 的描述中,正确的是( )
A.图象必经过点(-2,1)
B.图象经过第一、二、三象限
C.当 x> 1 时,y<0
2
D.y 随 x 的增大而增大
k - 2
2. 若 有意义,则函数 y=kx-1 的图象不经过第 象限.
3. 如果直线 y=ax+b 经过第一、三、四象限,那么直线 y=bx+a
8
经过第
象限,直线 y = - b x 经过第
a
象限.
8
y
O x
y=2kx
4. 正比例函数 y=2kx 的图象如图所示,则 y=(k-2)x+1-k 的图象可能是( )
y
O
x
y
O
x
y
O x
y
O
x
A. B. C. D.
5. 一次函数 y=mx+2 与正比例函数 y=2mx(m 为常数,且 m≠0) 在同一平面直角坐标系中的图象可能是( )
y
O
x
y
O
x
y
O
x
y
O
x
A. B. C. D.
6. 两条直线y1=ax+b 与y2=bx+a 在同一平面直角坐标系中的图象可能是( )
y
O
x
y
O
x
y
O x
y
O
x
8
A. B. C. D.
8
1. 一次函数 y=kx+k 在平面直角坐标系中的图象可能是( )
y
O x
y
O
x
y
O
x
y
O
x
A. B. C. D.
2. 一次函数 y=mx-n 与正比例函数 y=mnx(m,n 为常数,且
mn≠0)在同一平面直角坐标系中的图象中,一定不正确的是
( )
y
O
x
y
O
x
y
O
x
y
O
x
A. B. C. D.
3. 已知一次函数 y = - 1 x +1的图象如图所示,回答下列问题:
2
(1)当-1≤x<1 时,y 的取值范围是 ;
(2)当 x>2 时,y 的取值范围是 ;
(3)当 01 时,x 的取值范围是 ;
(3)当-1≤y<2 时,x 的取值范围是 .
y
2
-1
O
x
8
8
1. 如图,直线 y1
= 1 x 与 y2=-x+3 相交于点 A,当 y1y2 时,x 的取值范围是 .
y
y1=x+b
P
-1 O
x
-1
y2=kx-1
3. 如图,直线 y1 = -x + m 与直线 y2=nx+4n(n≠0)的交点的横坐标为-2,回答下列问题:
(1)当 y1>y2 时,x 的取值范围是 ;
(2)当 y2>0 时,x 的取值范围是 .
y
y2=nx+4n
-2 O x
y1=-x+m
8
Ø 思考小结
1. 一次函数图象分析
①只有一个一次函数图象时,根据函数的性质,判断 k,b 的符号.
②多个一次函数共存时,可以先假设其中一个正确,根据函数的性质,判断 _的符号,然后用 _的符号去验证
.
y
B
O
x
A
2. 如图,直线 y = kx + b 经过 A(-2,-1),B(-3,0)两点,则当
1
x < kx + b < 0 时,x 的取值范围是 .
2
思路分析:
① 观察图形,发现图中缺少 y = 1 x 的图象,考虑作出函数
2
8
y = 1 x 的图象,图象刚好过点
2
(填“A”或“B”);
8
②通过找交点, , ,求 x 的取值范围.首先,三条直线的交点分别是 ,然后过交点 作直线,分析得 x 的取值范围是 .
8
【参考答案】
Ø 巩固练习
1. C
2. 二
3. 一、二、四,一、三
4. B
5. A
6. A
7. A
8. A
9. (1) 1 < y ≤ 3 ;(2)y<0;(3) - 1 ≤ y < 1 ;(4)x≤2
2 2 2
10. (1) 0 ≤ y < 2 ;(2) x >- 1 ;(3) - 3 ≤ x < 0
2 2
11. x < 2
12. x > -1
13. x < -2 ; x > -4
Ø 思考小结
1. ②k,b;k,b,另一个图象存在的合理性
2. -3 < x < -2
①划直线,定左右, x > -3 ;
②A
③找交点,划直线,定左右, x < -2
-3 < x < -2
8
相关文档
- 2020年精选的初中语文教师实习自我2021-06-03 02:16:0912页
- 数学(心得)之初中数学高效课堂的实施2021-06-03 02:11:457页
- 历史(心得)之如何培养初中学生学习历2021-06-03 02:01:504页
- 年度工作总结-初中英语教师年度考2021-06-03 01:56:344页
- 数学(心得)之初中数学作业批改的几点2021-06-03 01:53:373页
- 初中一年级化学教师工作总结范文(通2021-06-03 01:48:354页
- 2020中考英语一轮复习 初中英语时2021-06-03 01:27:398页
- 美术(心得)之论欣赏评述课在初中美术2021-06-03 00:54:5311页
- 北师大版初中数学确定一次函数表达2021-06-03 00:48:204页
- 2020年初中化学第一学期的教学计划2021-06-03 00:41:527页