2016年甘肃省张掖市肃南一中高考模拟数学文 17页

2016 年甘肃省张掖市肃南一中高考模拟数学文 一.选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1. 设集合 A={x|x2+x-6≤0}，集合 B 为函数 1 1 y x   的定义域，则 A∩B=( ) A.(1，2) B.[1，2] C.[1，2) D.(1，2] 解析： A={x|x2+x-6≤0}={x|-3≤x≤2}=[-3，2]， 要使函数 1 1 y x   有意义，则 x-1＞0，即 x＞1， ∴函数的定义域 B=(1，+∞)， 则 A∩B=(1，2]. 答案：D. 2. 若复数 z 满足 iz=2+4i，则在复平面内，z 对应的点的坐标是( ) A.(2，4) B.(2，-4) C.(4，-2) D.(4，2) 解析：复数 z 满足 iz=2+4i，则有  2424 421 iiizii   ， 故在复平面内，z 对应的点的坐标是(4，-2). 答案：C. 3. 一枚质地均匀的正方体骰子，六个面上分别刻着 1 点至 6 点.甲、乙二人各掷骰子一次， 则甲掷得的向上的点数比乙大的概率为( ) A. 2 9 B. 1 4 C. 5 12 D. 1 2 解析：甲、乙二人各掷骰子一次，得到所有的基本事件有 共 36 种， 显然甲掷得的向上的点数比乙大的有 15 种， 故甲掷得的向上的点数比乙大的概率为 P= 15 36 ＝ 5 12 . 故选：C. 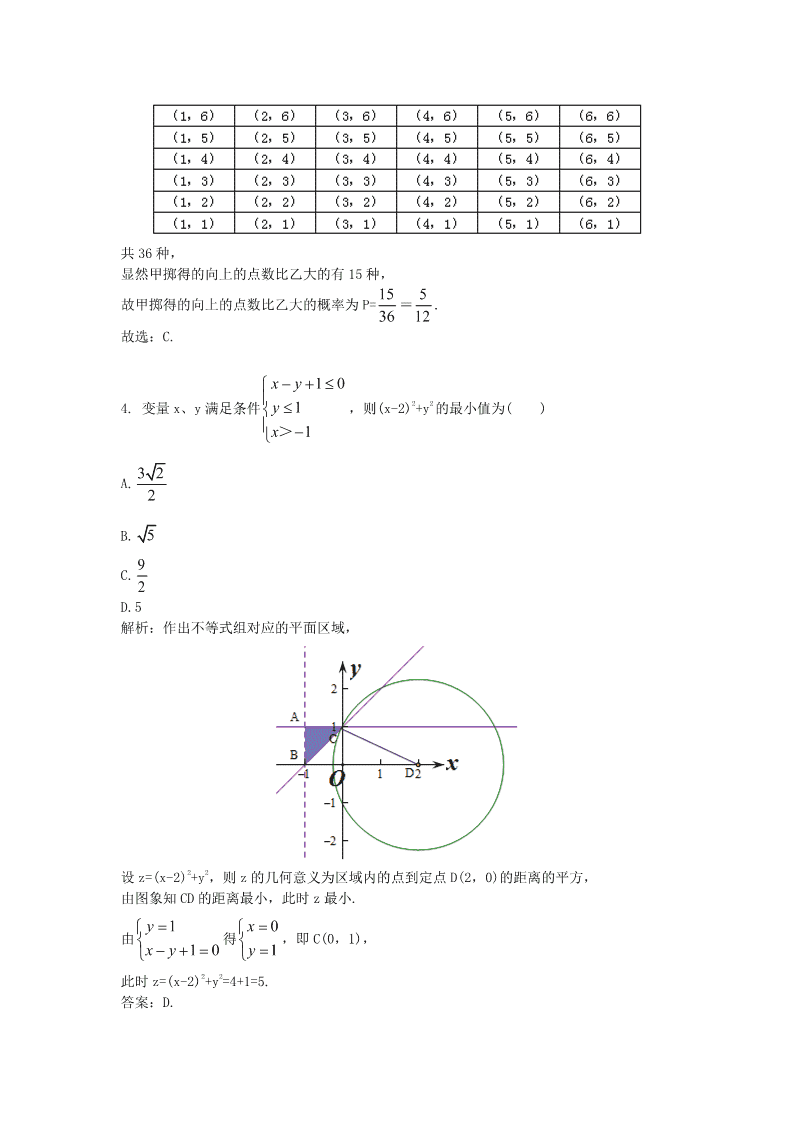4. 变量 x、y 满足条件 10 1 1 xy y x        ＞ ，则(x-2)2+y2 的最小值为( ) A. 32 2 B. 5 C. 9 2 D.5 解析：作出不等式组对应的平面区域， 设 z=(x-2)2+y2，则 z 的几何意义为区域内的点到定点 D(2，0)的距离的平方， 由图象知 CD 的距离最小，此时 z 最小. 由 1 10 y xy    得 0 1 x y    ，即 C(0，1)， 此时 z=(x-2)2+y2=4+1=5. 答案：D. 5. 将函数 y＝sin(x+ 6  )(x∈R)的图象上所有的点向左平移 4  个单位长度，再把图象上各 点的横坐标扩大到原来的 2 倍，则所得的图象的解析式为( ) A.y＝sin(2x+ 5 12  )(x∈R) B.y＝sin( 2 x + )(x∈R) C.y＝sin( - 12  )(x∈R) D.y＝sin( + 5 24  )(x∈R) 解析：将函数 y＝sin(x+ )(x∈R)的图象上所有的点向左平移 个单位长度，得到函数 y ＝sin(x+ + )＝sin(x+ )， 再把图象上各点的横坐标扩大到原来的 2 倍，得到函数 y＝sin( + )(x∈R). 答案：B. 6. 某校通过随机询问 100 名性别不同的学生是否能做到“光盘”行动，得到所示联表： 附：K2=  211 22 12 21 1 2 1 2 n n n n n n n n n      ，则下列结论正确的是( ) A.在犯错误的概率不超过 1%的前提下，认为“该校学生能否做到‘光盘’与性别无关” B.有 99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” C.在犯错误的概率不超过 10%的前提下，认为“该校学生能否做到‘光盘’与性别有关” D.有 90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” 解析：由 2×2 列联表得到 a=45，b=10，c=30，d=15. 则 a+b=55，c+d=45，a+c=75，b+d=25，ad=675，bc=300，n=100. 代入 K2=        2n adbc abcdacbd   ， 得 K2 的观测值 k=  2100 675 300 55 45 75 25     . 因为 2.706＜3.030＜3.841. 所以有 90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”. 即在犯错误的概率不超过 10%的前提下，认为“该校学生能否做到‘光盘’与性别有关”. 答案：C. 7. 已知向量 a ＝(sinθ，-2)，b ＝(1，cosθ)，且 a ⊥ ，则 sin2θ+cos2θ的值为( ) A.1 B.2 C. 1 2 D.3 解析：由题意可得 ab =sinθ-2cosθ=0，即 tanθ=2. ∴sin2θ+cos2θ= 2 22 2 sincoscos cossin     = 2 21 1 tan tan     =1. 答案：A. 8. 如图所示程序框图中，输出 S=( ) A.45 B.-55 C.-66 D.66 解析：由程序框图知，第一次运行 T=(-1)2·12=1，S=0+1=1，n=1+1=2； 第二次运行 T=(-1)3·22=-4，S=1-4=-3，n=2+1=3； 第三次运行 T=(-1)4·32=9，S=1-4+9=6，n=3+1=4； … 直到 n=9+1=10 时，满足条件 n＞9，运行终止，此时 T=(-1)10·92， S=1-4+9-16+…+92-102=1+(2+3)+(4+5)+(6+7)+(8+9)-100=19 2  ×9-100=-55. 答案：B. 9. 某几何体的三视图如图所示，且该几何体的体积是 3，则正视图中的 x 的值是( ) A.2 B. 9 2 C. 3 2 D.3 解析：根据三视图判断几何体为四棱锥，其直观图是： V= 1 3 × 12 2  ×2×x=3  x=3. 答案：D. 10. 如图可能是下列哪个函数的图象( ) A.y=2x-x2-1 B.y= 2 41 x sinx x  C.y=(x2-2x)ex D.y= x lnx 解析：A 中，∵y=2x-x2-1，当 x 趋向于-∞时，函数 y=2x 的值趋向于 0，y=x2+1 的值趋向+∞， ∴函数 y=2x-x2-1 的值小于 0，∴A 中的函数不满足条件； B 中，∵y=sinx 是周期函数，∴函数 y= 2 41 x sinx x  的图象是以 x 轴为中心的波浪线， ∴B 中的函数不满足条件； C 中，∵函数 y=x2-2x=(x-1)2-1，当 x＜0 或 x＞2 时，y＞0，当 0＜x＜2 时，y＜0； 且 y=ex＞0 恒成立， ∴y=(x2-2x)ex 的图象在 x 趋向于-∞时，y＞0，0＜x＜2 时，y＜0，在 x 趋向于+∞时，y 趋 向于+∞； ∴C 中的函数满足条件； D 中，y= 的定义域是(0，1)∪(1，+∞)，且在 x∈(0，1)时，lnx＜0， ∴y= ＜0，∴D 中函数不满足条件. 答案：C. 11. 已知中心在原点的椭圆与双曲线有公共焦点，左、右焦点分别为 F1、F2，且两条曲线在 第一象限的交点为 P，△PF1F2 是以 PF1 为底边的等腰三角形.若|PF1|=10，椭圆与双曲线的离 心率分别为 e1、e2，则 e1·e2+1 的取值范围为( ) A.(1，+∞) B.( 4 3 ，+∞) C.( 6 5 ，+∞) D.( 10 9 ，+∞) 解析：设椭圆和双曲线的半焦距为 c，|PF1|=m，|PF2|=n，(m＞n)， 由于△PF1F2 是以 PF1 为底边的等腰三角形.若|PF1|=10， 即有 m=10，n=2c， 由椭圆的定义可得 m+n=2a1， 由双曲线的定义可得 m-n=2a2， 即有 a1=5+c，a2=5-c，(c＜5)， 再由三角形的两边之和大于第三边，可得 2c+2c=4c＞10， 则 c＞ 5 2 ，即有 ＜c＜5. 由离心率公式可得 e1·e2= 1 c a · 2 c a = 2 225 c c = 2 1 25 1c  ， 由于 1＜ 2 25 c ＜4，则有 2 1 25 1c  ＞ 1 3 . 则 e1·e2+1＞ +1＝ 4 3 . ∴e1·e2+1 的取值范围为( ，+∞). 答案：B. 12. 若 a 是 f(x)=sinx-xcosx 在 x∈(0，2π)的一个零点，则  x∈(0，2π)，下列不等式 恒成立的是( ) A. sinx x ≥ sina a B.cosa≥ C. 3 2  ≤a≤2π D.a-cosa≥x-cosx 解析：f′(x)=xsinx， 当 x∈(0，π)，f′(x)＞0，函数 f(x)单调递增， 当 x∈(π，2π)，f′(x)＜0，函数 f(x)单调递减， 又 f(0)=0，f(π)＞0，f(2π)＜0， ∴a∈(π，2π)， ∴当 x∈(0，a)，f(x)＞0，当 x∈(a，2π)，f(x)＜0， 令 g(x)= ，g′(x)= 2 xcosxsinx x  ， ∴当 x∈(0，a)，g′(x)＜0，函数 g(x)单调递减，当 x∈(a，2π)，g′(x)＞0，函数 g(x) 单调递增， ∴g(x)≥g(a). 答案：A. 二.填空题(本大题共 4 个小题，每小题 5 分，共 20 分.) 13. 在△ABC 中，角 A，B，C 所对边分别为 a，b，c，且 c＝ 42，B=45°，面积 S=2，则 b 等于_____. 解析：∵c＝ ，B=45°，面积 S=2， ∴S= 1 2 acsinB= 1 2 ×a× × 2 2 =2a=2. ∴a=1 由余弦定理得 b2=a2+c2-2accosB=12+( )2-2×1× × =25 ∴b=5. 答案：5. 14. 已知三棱柱 ABC-A1B1C1 的侧棱和底面垂直，且所有棱长都相等，若该三棱柱的各顶点都 在球 O 的表面上，且球 O 的表面积为 7π，则此三棱柱的体积为_____. 解析：如图， ∵三棱柱 ABC-A1B1C1 的所有棱长都相等，6 个顶点都在球 O 的球面上， ∴三棱柱为正三棱柱，且其中心为球的球心，设为 O， 再设球的半径为 r，由球 O 的表面积为 7π，得 4πr2=7π，∴r= 7 2 . 设三棱柱的底面边长为 a，则上底面所在圆的半径为 3 3 a，且球心 O 到上底面中心 H 的距 离 OH= 2 a ， ∴r2=( )2+( a)2，即 r= 7 12 a， ∴a= 3. 则三棱柱的底面积为 S= 3 4 ×( 3 )2= 33 4 . ∴VABC-A1B1C1= × = 9 4 . 答案： . 15. 在直角三角形 ABC 中，∠ACB=90°，AC=BC=2，点 P 是斜边 AB 上的一个三等分点，则 CP ·CB + CP ·CA =_____. 解析：由题意可建立如图所示的坐标系 可得 A(2，0)B(0，2)，P( 2 3 ， 4 3 )或 P( ， )， 故可得 CP =( ， )或( ， )， CA =(2，0)， CB =(0，2)， 所以 + CB =(2，0)+(0，2)=(2，2)， 故 CP · + CP · = CP ·( + )=( ， )·(2，2)=4 或=( ， )·(2，2)=4. 答案：4. 16. 已知函数 f(x)＝ 2 2 () () 1 7 14 1 x ax x a x a x       ＞ ，若  x1，x2∈R，且 x1≠x2，使得 f(x1)=f(x2)， 则实数 a 的取值范围是_____. 解析：由题意， 2 2 12 7 144 a a aa       ＜ ＞ 或 2 12 1714 a aaa   ＞ ＞ ∴a＜2 或 3＜a＜5. 答案：(-∞，2)∪(3，5). 三.解答题：本大题共 5 小题，共 70 分，解答应写出文字说明，证明过程或演算步骤. 17. 已知等比数列{an}的前 n 项和为 Sn，an＞0，a1= 2 3 ，且 2 3 a ， 3 1 a ， 4 1 a 成等差数列. (Ⅰ)求数列{an}的通项公式； (Ⅱ)设数列{bn}满足 bn·log3(1-Sn+1)=1，求适合方程 b1b2+b2b3+…+bnbn+1= 25 51 的正整数 n 的值. 解析：(Ⅰ)由 ， ， 成等差数列建立关于 q 的方程，解出 q，即可求数列{an}的通 项公式； (Ⅱ)利用前 n 项和公式表示出 Sn+1，从而表示出 bn，利用裂项相消法求出 b1b2+b2b3+…+bnbn+1， 建立关于 n 的方程，求解即可. 答案：(Ⅰ)设数列{an}的公比 q， 由 2 3 a ， 3 1 a ， 4 1 a 成等差数列， 得-3+ 2 1 q ＝ 2 q ， 解得 q＝ 1 3 或 q=-1(舍去)， ∴an＝2×( )n； (Ⅱ)∵Sn+1＝ 1 21133 11 3 n    ＝ 1 11 3 n  ， ∴log3(1-Sn+1)＝log3 1 1 3 n  =-n-1， ∴bn＝ 1 1n  ， bnbn+1＝    1 12nn ＝ 11 12nn ， b1b2+b2b3+…+bnbn+1＝ 1 2 - 1 3 + - 1 4 +…+ = - 1 2n  = 25 51 . 解得：n=100. 18. 2014 年“五一”期间，高速公路车辆较多.某调查公司在一服务区从七座以下小型汽 车中按进服务区的先后每间隔 50 辆就抽取一辆的抽样方法抽取 40 名驾驶员进行询问调查， 将他们在某段高速公路的车速(km/t)分成六段：[60，65)，[65，70)，[70，75)，[75，80)， [80，85)，[85，90)后得到如图所示的频率分布直方图. (Ⅰ)求这 40 辆小型车辆车速的众数及平均车速(可用中值代替各组数据平均值)； (Ⅱ)若从车速在[60，70)的车辆中任抽取 2 辆，求车速在[65，70)的车辆至少有一辆的概率. 解析：(1)众数的估计值为最高的矩形的中点，即众数的估计值等于 77.5，然后求解这 40 辆小型车辆的平均车速. (2)从图中可知，车速在[60，65)的车辆数，车速在[65，70)的车辆数，设车速在[60，65) 的车辆设为 a，b，车速在[65，70)的车辆设为 c，d，e，f，列出所有基本事件，车速在[65， 70)的车辆数，然后求解概率. 答案：(1)众数的估计值为最高的矩形的中点，即众数的估计值等于 77.5 这 40 辆小型车辆的平均车速为： 262.5467.5872.51277.51082.5487.5 40  ＝77(km/t) (2)从图中可知，车速在[60，65)的车辆数为：m1=0.01×5×40=2(辆) 车速在[65，70)的车辆数为：m2=0.02×5×40=4(辆) 设车速在[60，65)的车辆设为 a，b，车速在[65，70)的车辆设为 c，d，e，f，则所有基本 事件有：(a，b)，(a，c)，(a，d)，(a，e)，(a，f)，(b，c)，(b，d)，(b，e)，(b，f)(c， d)，(c，e)，(c，f)，(d，e)，(d，f)(e，f)共 15 种 其中车速在[65，70)的车辆至少有一辆的事件有：(a，c)，(a，d)，(a，e)，(a，f)，(b， c)，(b，d)，(b，e)，(b，f)，(c，d)，(c，e)，(c，f)，(d，e)，(d，f)，(e，f)，共 14 种 所以，车速在[65，70)的车辆至少有一辆的概率为 P＝ 14 15 . 19. 如图，在多面体 ABCDEF 中，底面 ABCD 是边长为 2 的正方形，四边形 BDEF 是矩形，平 面 BDEF⊥平面 ABCD，BF=3，G 和 H 分别是 CE 和 CF 的中点. (Ⅰ)求证：AC⊥平面 BDEF； (Ⅱ)求证：平面 BDGH∥平面 AEF； (Ⅲ)求多面体 ABCDEF 的体积. 解析：(I)由面面垂直的性质可证 AC 与平面 BDEF 垂直； (II)利用线线平行证明 GH∥平面 AEF，OH∥平面 AEF.由面面平行的判定定理可证面面平行； (III)把多面体分割成四棱锥 A-BDEF 和四棱锥 C-BDEF，分别求出体积，再求和. 答案：(Ⅰ)证明：∵四边形 ABCD 是正方形， ∴AC⊥BD. 又∵平面 BDEF⊥平面 ABCD，平面 BDEF∩平面 ABCD=BD， 且 AC 平面 ABCD， ∴AC⊥平面 BDEF； (Ⅱ)证明：在△CEF 中， ∵G、H 分别是 CE、CF 的中点， ∴GH∥EF， 又∵GH  平面 AEF，EF  平面 AEF， ∴GH∥平面 AEF， 设 AC∩BD=O，连接 OH，在△ACF 中， ∵OA=OC，CH=HF， ∴OH∥AF， 又∵OH  平面 AEF，AF  平面 AEF， ∴OH∥平面 AEF. 又∵OH∩GH=H，OH、GH  平面 BDGH， ∴平面 BDGH∥平面 AEF. (Ⅲ)由(Ⅰ)，得 AC⊥平面 BDEF， 又∵AO= 2 ，四边形 BDEF 的面积 S=3×2 =6 ， ∴四棱锥 A-BDEF 的体积 V1= 1 3 ×AO×S=4， 同理，四棱锥 C-BDEF 的体积 V2=4. ∴多面体 ABCDEF 的体积 V=8. 20. 已知椭圆 C1： 22 22 yx ab =1(a＞b＞0)的离心率 e= 3 3 ，且经过点(1， 6 2 )，抛物线 C2： x2=2py(p＞0)的焦点 F 与椭圆 C1 的一个焦点重合. (Ⅰ)过 F 的直线与抛物线 C2 交于 M，N 两点，过 M，N 分别作抛物线 C2 的切线 l1，l2，求直 线 l1，l2 的交点 Q 的轨迹方程； (Ⅱ)从圆 O：x2+y2=5 上任意一点 P 作椭圆 C1 的两条切线，切点为 A，B，证明：∠APB 为定 值，并求出这个定值. 解析：(Ⅰ)设椭圆的半焦距为 c，以及 c a ＝ ，设椭圆方程为 22 223 2 yx c c ＝1，将点(1， )的坐标代入得 c，然后求解椭圆方程，求出抛物线方程，设直线 MN：y=kx+1，M(x1， y1)，N(x2，y2)，代入抛物线方程得 x2-4kx-4=0，利用韦达定理结合函数的导数求解直线的 斜率，直线方程，求出点 Q 的横坐标是 1 2 (x1+x2)，点 Q 的纵坐标，然后求解点 Q 的轨迹方 程. (Ⅱ)①当两切线的之一的斜率不存在时，根据对称性，设点 P 在第一象限，求解∠APB 的大 小为定值. ②当两条切线的斜率都存在时，即 x≠± 2 时，设 P(x0，y0)，切线的斜率为 k，则切线方 程与椭圆方程联立，利用△=0，切线 PA，PB 的斜率 k1，k2 是上述方程的两个实根，通过 k1k2 ＝ 0 2 0 2 3 3 y x   ，求解∠APB 的大小为定值 2  . 答案：(Ⅰ)设椭圆的半焦距为 c，则 c a ＝ 3 3 ，即 a＝ 3 c，则 b＝ 2 c， 椭圆方程为 22 223 2 yx c c ＝1，将点(1， 6 2 )的坐标代入得 c2=1， 故所求的椭圆方程为 22 3 2 yx ＝1 焦点坐标为(0，±1)， 故抛物线方程为 x2=4y 设直线 MN：y=kx+1，M(x1，y1)，N(x2，y2)，代入抛物线方程得 x2-4kx-4=0， 则 x1+x2=4k，x1x2=-4，由于 y＝ 1 4 x2，所以 y′＝ 1 2 x，故直线 l1 的斜率为 x1，l1 的方程为 y- x2 1＝ x1(x-x1)，即 y＝ x1x- x2 1， 同理 l2 的方程为 y＝ x2x- x2 2 ， 令 x1x- x2 1＝ x2x- x2 2，即(x1-x2)x＝ (x1-x2)(x1+x2)，显然 x1≠x2， 故 x＝ (x1+x2)，即点 Q 的横坐标是 (x1+x2)， 点 Q 的纵坐标是 y＝ x1x- x2 1＝ x1(x1+x2)- x2 1＝ x1x2＝-1，即点 Q(2k，-1)， 故点 Q 的轨迹方程是 y=-1 (Ⅱ)证明：①当两切线的之一的斜率不存在时，根据对称性，设点 P 在第一象限， 则此时 P 点横坐标为 2 ，代入圆的方程得 P 点的纵坐标为 3 ， 此时两条切线方程分别为 x＝ 2 ，y＝ 3 ，此时∠APB＝ 2  ， 若∠APB 的大小为定值，则这个定值只能是 ②当两条切线的斜率都存在时，即 x≠± 时，设 P(x0，y0)，切线的斜率为 k， 则切线方程为 y-y0=k(x-x0)， 与椭圆方程联立消元得(3+2k2)x2+4k(y0-kx0)x+2(kx0-y0)2-6＝0 由于直线 y-y0=k(x-x0)是椭圆的切线， 故△＝[4k(y0-kx0)]2-4(3+2k2)[2(kx0-y0)2-6]＝0， 整理得(2-x2 0)k2+2x0y0k-(y2 0 -3)＝0 切线 PA，PB 的斜率 k1，k2 是上述方程的两个实根，故 k1k2＝ 2 0 2 0 3 2 y x   ， 点 P 在圆 x2+y2=5 上，故 y2 0 -3＝2-x2 0 ，所以 k1k2=-1，所以∠APB＝ 2  . 综上可知：∠APB 的大小为定值 ，得证 21. 已知函数 f(x)的导函数 f′(x)=x2+2ax+b(ab≠0)，且 f(0)=0.设曲线 y=f(x)在原点处 的切线 l1 的斜率为 k1，过原点的另一条切线 l2 的斜率为 k2. (1)若 k1：k2=4：5，求函数 f(x)的单调区间； (2)若 k2=tk1 时，函数 f(x)无极值，且存在实数 t 使 f(b)＜f(1-2t)成立，求实数 a 的取值 范围. 解析：(1)利用函数的导数，求出 k1=f'(0)=b，设 l2 与曲线 y=f(x)的切点为(x0，y0)(x0≠0)， 利用斜率相等推出 b=-3a2，化简 f'(x)=x2+2ax-3a2=(x+3a)(x-a)，通过①当 a＞0 时，②当 a ＜0 时，分别求解单调区间. (2)由(1)若 k2=tk1，利用 f(x)无极值，△＝ 2 2 34 1 aa t  ≤0，求出 t 的范围，利用 f(b)＜ f(1-2t)，推出 3a2＜4(1-t)(1-2t)，然后求解 a 的范围. 答案：(1)由已知 f(x)＝ 1 3 x3+ax2+bx，k1=f'(0)=b，设 l2 与曲线 y=f(x)的切点为(x0，y0)(x0 ≠0) 则 x2 0+2ax0+b＝ 0 0 y x ＝ 1 3 x2 0 +ax0+b 所以 2 3 x2 0+ax0＝0，即 x0＝- 3 2 a， 则 k2＝f′(- a)＝ 9 4 a2-3a2+b＝- 3 4 a2+b. 又 4k2=5k1，所以-3a2+4b=5b，即 b=-3a2 因此 f'(x)=x2+2ax-3a2=(x+3a)(x-a) ①当 a＞0 时，f(x)的增区间为(-∞，-3a)和(a，+∞)，减区间为(-3a，a). ②当 a＜0 时，f(x)的增区间为(-∞，a)和(-3a，+∞)，减区间为(a，-3a). (2)由(1)若 k2=tk1，则- a2+b＝tb，∵ab≠0，∴t≠1， 于是 b＝   23 41 a t ，所以 f′(x)＝x2+2ax+ ， 由 f(x)无极值可知，△＝ ≤0，即 214 1 t at   ≤0， 所以 14 1 t t   ≤0， 1 4 ≤t＜1 由 f(b)＜f(1-2t)知，b＜1-2t，即   23 41 a t ＜1-2t， 就是 3a2＜4(1-t)(1-2t)， 而 ≤t＜1，故{4(1-t)(1-2t)}max＝ 3 2 ，所以 3a2＜ ， 又 a≠0，因此 a∈(- 2 2 ，0)∪(0， ). 请考生在第 22、23、24 三题中任选一题作答，如果多做，则按所做的第一题记分.答题时 用 2B 铅笔在答题卡上把所选题目的题号涂黑.【选修 4-1：几何证明选讲】 22. 如图，⊙O 的半径为 6，线段 AB 与⊙相交于点 C、D，AC=4，∠BOD=∠A，OB 与⊙O 相交 于点. (1)求 BD 长； (2)当 CE⊥OD 时，求证：AO=AD. 解析：(1)证明△OBD∽△AOC，通过比例关系求出 BD 即可. (2)通过三角形的两角和，求解角即可. 答案：(1)∵OC=OD，∴∠OCD=∠ODC，∴∠OAC=∠ODB. ∵∠BOD=∠A，∴△OBD∽△AOC.∴ BD OC ＝ OD AC ， ∵OC=OD=6，AC=4，∴ 6 BD ＝ 6 4 ，∴BD=9. (2)证明：∵OC=OE，CE⊥OD.∴∠COD=∠BOD=∠A. ∴∠AOD=180°-∠A-∠ODC=180°-∠COD-∠OCD=∠ADO. ∴AD=AO. 【选修 4-4：坐标系与参数方程】 23. 在平面直角坐标系 xoy 中，以 O 为极点，x 轴的正半轴为极轴的极坐标系中，直线 l 的 极坐标方程为θ= 4  ，曲线 C 的参数方程为 2xcos ysin    ＝ ＝ . (1)写出直线 l 与曲线 C 的直角坐标方程； (2)过点 M 平行于直线 l1 的直线与曲线 C 交于 A、B 两点，若|MA|·|MB|= 8 3 ，求点 M 轨迹的 直角坐标方程. 解析：(1)利用极坐标与直角坐标方程的互化，直接写出直线 l 的普通方程，消去参数可得 曲线 C 的直角坐标方程； (2)设点 M(x0，y0)以及平行于直线 l1 的直线参数方程，直线 l1 与曲线 C 联立方程组，通过 |MA|·|MB|= 8 3 ，即可求点 M 轨迹的直角坐标方程.通过两个交点推出轨迹方程的范围. 答案：(1)直线 l 的极坐标方程为θ= 4  ，所以直线斜率为 1，直线 l：y=x； 曲线 C 的参数方程为 x＝ 2x c os y sin    ＝ ＝ .消去参数θ， 可得曲线 C： 2 2 12 x y ＝ (2)设点 M(x0，y0)及过点 M 的直线为 l1： 0 0 2 2 2 2 xx y ty t      ＝ ＝ 由直线 l1 与曲线 C 相交可得： 22 00 2 002222 223 txtyxt y ＝0 |MA|·|MB|＝  | 22 0022 3 2 xy|＝ ，即：x0 2+2y0 2＝6， x2+2y2=6 表示一椭圆 取 y=x+m 代入 得：3x2+4mx+2m2-2=0 由△≥0 得- 3 ≤m≤ 3 故点 M 的轨迹是椭圆 x2+2y2=6 夹在平行直线 y＝x± 3 之间的两段弧. 【选修 4-5：不等式选讲】 24. 已知函数 f(x)=|2x-a|+|2x+3|，g(x)=|x-1|+2. (1)解不等式|g(x)|＜5； (2)若对任意 x1∈R，都有 x2∈R，使得 f(x1)=g(x2)成立，求实数 a 的取值范围. 解析：(1)利用||x-1|+2|＜5，转化为-7＜|x-1|＜3，然后求解不等式即可. (2)利用条件说明{y|y=f(x)}  {y|y=g(x)}，通过函数的最值，列出不等式求解即可. 答案：(1)由||x-1|+2|＜5，得-5＜|x-1|+2＜5 ∴-7＜|x-1|＜3， 得不等式的解为-2＜x＜4 (2)因为任意 x1∈R，都有 x2∈R，使得 f(x1)=g(x2)成立， 所以{y|y=f(x)}  {y|y=g(x)}， 又 f(x)=|2x-a|+|2x+3|≥|(2x-a)-(2x+3)|=|a+3|， g(x)=|x-1|+2≥2，所以|a+3|≥2，解得 a≥-1 或 a≤-5， 所以实数 a 的取值范围为 a≥-1 或 a≤-5.