- 971.50 KB
- 2021-06-03 发布
数学(文科)试题
第Ⅰ卷(选择题 满分60分)
一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 为虚数单位,复数的虚部是( )
A. B.2 C. D.-1
2.设集合,,则( )
A. B. C. D.
3.已知抛物线的焦点与圆的圆心重合,则抛物线的方程是( )
A. B. C. D.
4.等差数列的前项的和为,且与是方程的两根,则( )
A.10 B.15 C. 20 D.40
5.按照图如图所示的程序框图执行,若输出结果为,则处条件是( )
A. B. C. D.
6.下列命题中真命题的个数是( )
(1)有两个互相平行,其余各面都是平行四边形的多面体是棱柱.
(2)四棱锥的四个侧面可以是直角三角形.
(3)用一个平面去截圆锥,得到一个圆锥和一个圆台.
(4)圆锥的轴截面是所有过圆锥顶点的截面中面积最大的.
A.1 B.2 C.3 D.4
7.将函数图象上所有点的横坐标变为原来的2倍,再向右平移个单位长度,得到函数的图象,则的图象的一条对称轴方程是( )
A. B. C. D.
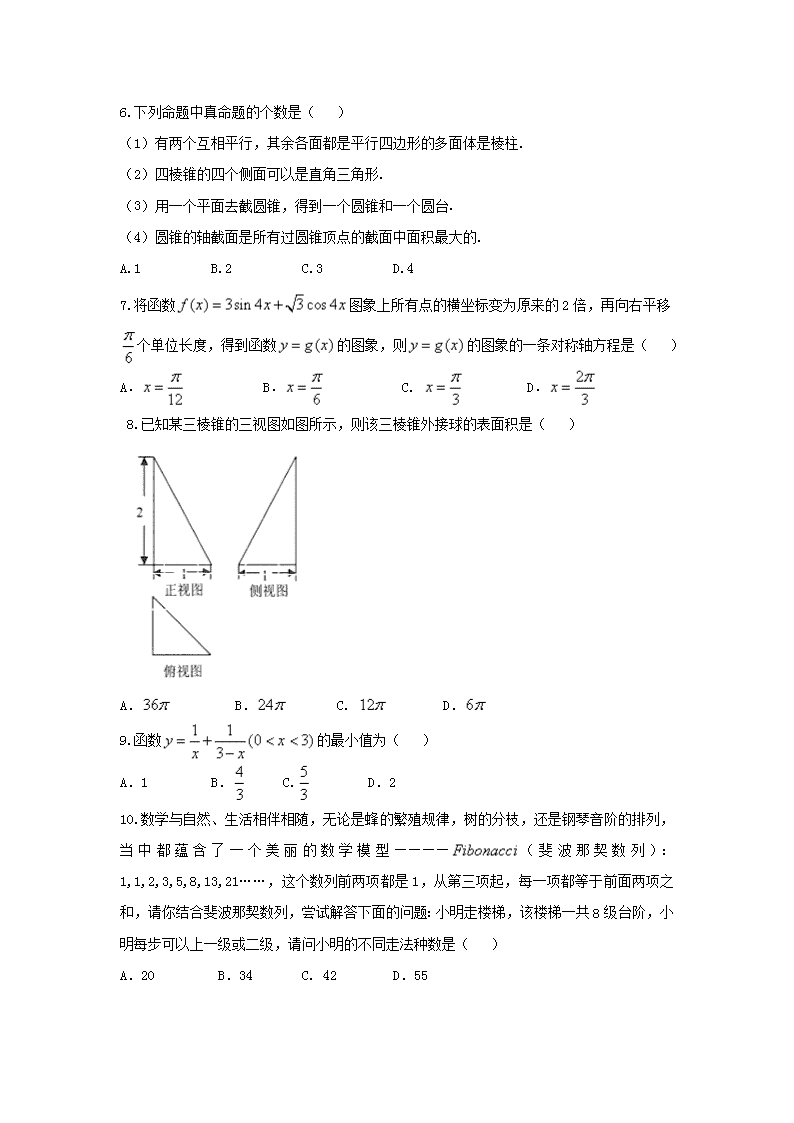
8.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )
A. B. C. D.
9.函数的最小值为( )
A.1 B. C. D.2
10.数学与自然、生活相伴相随,无论是蜂的繁殖规律,树的分枝,还是钢琴音阶的排列,当中都蕴含了一个美丽的数学模型 ————(斐波那契数列):1,1,2,3,5,8,13,21……,这个数列前两项都是1,从第三项起,每一项都等于前面两项之和,请你结合斐波那契数列,尝试解答下面的问题:小明走楼梯,该楼梯一共8级台阶,小明每步可以上一级或二级,请问小明的不同走法种数是( )
A.20 B.34 C. 42 D.55
11.设双曲线的右顶点为,右焦点为 ,弦过且垂直于轴,过点、点分别作直线 、的垂线,两垂线交于点,若到直线的距离小于,则该双曲线离心率的取值范围是( )
A. B. C. D.
12.已知函数,则关于的方程(为实数)根个数不可能为( )
A.2 B.3 C. 4 D.5
第Ⅱ卷(非选择题 满分90分)
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置上)
13.某人午睡醒来,发现手表停了,他打开收音机,想听电台报时(假设电台是整点报时),则他等待试卷不多于10分钟的概率为 .
14.已知点,点的坐标满足不等式组 ,则的取值范围是 .
15.在中,,,,则 .
16.已知定义在上的函数满足恒成立,且(为自然对数的底数),则不等式的解集为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.)
17.(本小题满分12分)
为了调查黄山市某校高中学生是否愿意在寒假期间参加志愿者活动,用简单随机抽样方法从该校调查了80人,结果如下:
(1)若用分层抽样的方法在愿意参加志愿者活动的学生抽取5人,则应女生中抽取多少人?
(2)在(1)中抽取出的5人中任选2人,求“被选中的恰好是一男一女”的概率.
注:
18. (本小题满分12分)
已知中,,,,且是的中点.
(1)求的长;
(2)如图,点是以为圆心角的劣弧上任意一点,求的取值范围.
19. (本小题满分12分)
正方形的边长为2,,将正方形沿对角线折起,使,得到三棱锥.
(1)点在棱上,且,点在棱上,且,求证:平面;
(2)当为何值时,三棱锥的体积最大?并求出最大值.
20. (本小题满分12分)
已知椭圆的左、右焦点分别为,点是椭圆上的一个动点,的周长为6,且存在点使得为正三角形.
(1)求椭圆的方程;
(2)若是椭圆上不重合的四个点,与相交于点,且.若的斜率为,求四边形的面积.
21.(本小题满分12分)
已知函数.
(1)求函数的单调区间;
(2)证明:.
考生注意:请考生在第22、23两题中任选一题做答,只能做所选定的题目,如果多做,则按所做的第一个题目计分.作答时,请用2B铅笔在答题卡上将所选题目后的方框涂黑.
22. (本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系中,直线 的参数方程是(是参数)
以原点为极点,为极轴建立极坐标系,圆 的极坐标方程为.
(1)求直线的普通方程和圆心 的直角坐标;
(2)求圆上的点到直线 距离的最小值.
23. (本小题满分10分)选修4-5:不等式选讲
已知函数,且不恒为0.
(1)若为奇函数,求值;
(2)若当 时,恒成立,求实数的取值范围.
黄山市2017届高中毕业班第一次质量检测
数学(文科)参考答案及评分标准
一、选择题
1-5: BCCAD 6-10: ACDBB 11、12:AD
二、填空题
13. 14. 15. 0 16.
三、解答题
17.(本小题满分12分)
其中恰好是一男一女的有6种:,
故所求概率是:.………………7分
(3)由题意:,
又,故有的把握认为“高中生是否愿意在寒假期间提供志愿者服务与性别有关”.………………12分
18.解:(1),
又,所以.………………5分
(2)设,,由题意:,
则在中,,………………9分
又,∴,又,即,
故.………………12分
19. (本小题满分12分)
解:(1)证明:取的中点,连接,
在中,,∴,又平面,平面,∴平面.
在中,∵分别是的中点,∴,又平面,平面,∴平面,,平面,
所以平面平面,平面,∴平面.………………6分
(2)∵,∴平面,
∴
.
所以当时,三棱锥的体积最大为,………………10分
此时, .………………12分
20.(本小题满分12分)
解:(1)设为椭圆的半焦距,依题意,有:解得,
∴.
故椭圆的方程为:.………………4分
(2)解:,又,则.
或,
∴.………………7分
,
∴.………………10分
∴,
故四边形的面积为.………………12分
21.(本小题满分12分)
解:(1)∵,∴.
又,∴由得:;∴由得:,
故的增区间是:;减区间是:.………………4分
(2)①由(1)可知:当时,是上的增函数,
∴当时,,
又当时,,∴.………………6分
∴.
将以上个式子两边分别相加得:
.………………8分
②构造函数,则.
∵,∴,则函数在上递减.
∴当时,.
又当时,,∴.………………10分
∴,
将以上个式子两边分别相加得:
.
综合①②得:.………………12分
22.(本小题满分10分)选修4—4:坐标系与参数方程
解:(1)直线的普通方程为; ┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉2分
又,,
圆的普通方程为,即,
圆心的直角坐标为. ┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉5分
(2)圆的半径,圆心到直线的距离,┉┉┉┉┉┉┉┉┉┉┉7分
又,圆上的点到直线距离最小值为2. ┉┉┉┉┉┉┉┉┉┉┉┉┉┉10分
23. (本小题满分10分)选修4—5:不等式选讲
解:(1)因为,若为奇函数,则由,得,
又不恒为0,得. ┉┉┉┉┉┉┉┉┉┉┉┉┉┉4分
此时,符合为奇函数,所以. ┉┉┉┉┉┉┉┉┉5分
(2)当时,恒成立,即在时恒成立
故在时恒成立, ┉┉┉┉┉┉┉┉┉┉┉┉┉8分
即.
而,,所以. ┉┉┉┉┉┉┉┉┉┉┉10分