- 535.50 KB
- 2021-06-03 发布
高二期中考试理科数学试题 5.23
一、单选题(每题5分)
1.把二进制数1101(2)化为十进制数是( )
A.5 B.13 C.25 D.26
2.为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分组数和分段的间隔分别为( )
A.50,20 B.40,25 C.25,40 D.20,50
3.在线段[0,3]上任取一点,则此点坐标不大于2的概率是( )
A. B. C. D.
4.4名同学选报文学、数学建模、街舞三个社团活动,每人报一项,共( )种报名方法.
A.81 B.64 C.36 D.12
5.袋中有三个红球,两个蓝球,现每次摸出一个球,不放回地摸取两次,则在第一次摸到蓝球的条件下,第二次摸到红球的概率为( )
A. B. C. D.
6.在一个6×6的表格中放3颗完全相同的白棋和3颗完全相同的黑棋,若这6颗棋子不在同一行也不在同一列上,则不同的放法有
A.14400种 B.518400种 C.720种 D.20种
7.三个元件正常工作的概率分别为,且是相互独立的。如图,将两个元件并联后再与元件串联接入电路,则电路不发生故障的概率是( )
A. B. C. D.
8.,则等于( )
A.32 B.-32 C.-33 D.-31
9.执行如图的程序框图,最后输出结果为8.若判断框填入的条件是,则实数的取值范围是( )
A. B. C. D.
10.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率为( )
A. B. C. D.
11.将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( ).
A.420 B.180 C.64 D.25
12.肇东一中五四青年节在礼堂上演了一个数学性节目,演员将一只鸽子用长为2米的绳子固定在一个棱长为4米的铁笼上顶中心位置(鸽子的飞行半径为2米),然后再将一只昆虫放入笼中,求鸽子能捉到昆虫的概率( )
A. B. C. D.
二、填空题(每题5分)
13.方程的正整数解的个数__________.
14.某高中对学生春节期间观看亚洲杯的调查,该校高一有800人,高二有900人,高三有1300人,现采用分层抽样随机抽取60人,则高三年级应抽取________人.
15.在今年的疫情防控期间,某省派出5个医疗队去支援武汉市的4个重灾区,每个重灾区至少分配一个医疗队,则不同的分配方案共有_____________种.(用数字填写答案)
16.将编号为1,2,3,4,5,6,7的七个小球放入编号为1,2,3,4,5,6,7的七个盒中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为______.
三、解答题(17题10分,18~22题每题12分)
17.从中任取个数,从中任取个数,
(1)能组成多少个没有重复数字的四位数?
(2)若将(1)中所有个位是的四位数从小到大排成一列,则第个数是多少?
18.(1)求的展开式中的常数项;
(2)已知的展开式中的系数为,求常数的值;
(3)求的展开式中的系数.
19.甲、乙、丙三名射击运动员射中目标的概率分别为、、,三人各射击一次,击中目标的次数记为.
(1)求甲、乙两人击中,丙没有击中的概率;
(2)求的分布列。
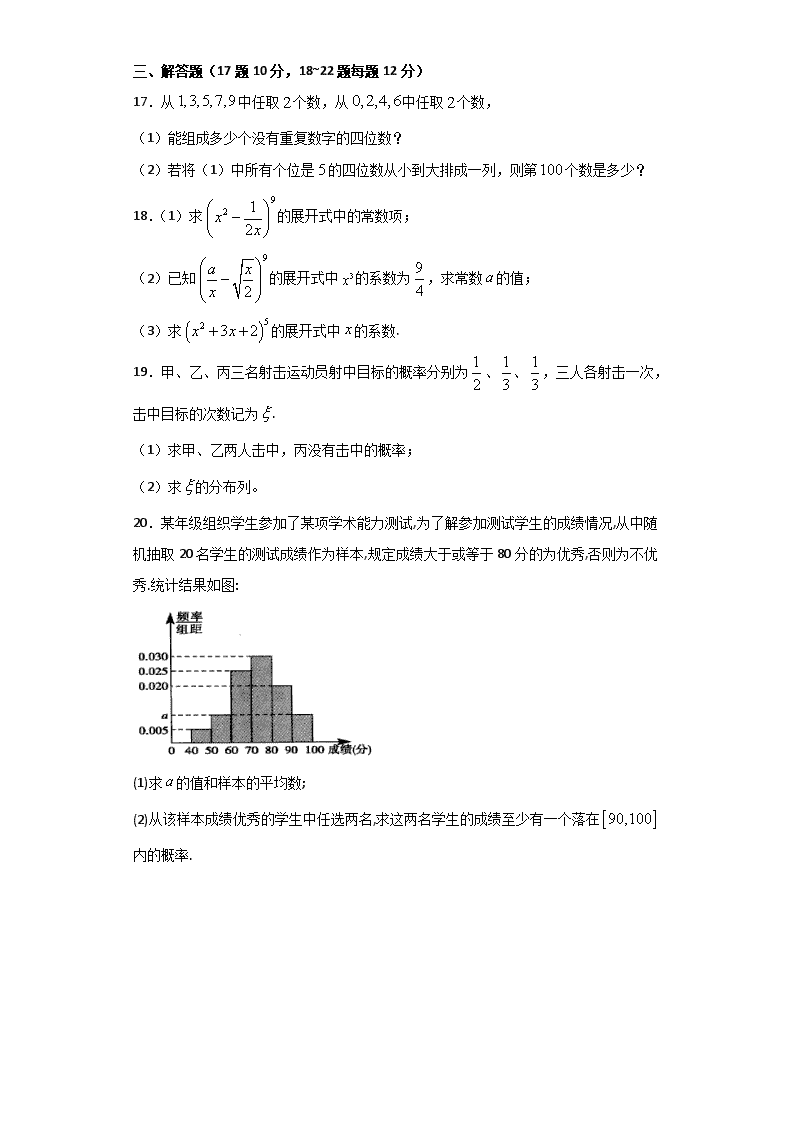
20.某年级组织学生参加了某项学术能力测试,为了解参加测试学生的成绩情况,从中随机抽取20名学生的测试成绩作为样本,规定成绩大于或等于80分的为优秀,否则为不优秀.统计结果如图:
(1)求的值和样本的平均数;
(2)从该样本成绩优秀的学生中任选两名,求这两名学生的成绩至少有一个落在内的概率.
21.中国改革开放以来经济发展迅猛,某一线城市的城镇居民2012~2018年人均可支配月收入散点图如下(年份均用末位数字减1表示).
(1)由散点图可知,人均可支配月收入y(万元)与年份x之间具有较强的线性相关关系,试求y关于x的回归方程(系数精确到0.001),依此相关关系预测2019年该城市人均可支配月收入;
(2)在2014~2018年的五个年份中随机抽取两个数据作样本分析,求所取的两个数据中,人均可支配月收入恰好有一个超过1万元的概率.
注:,,
22.某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为,且甲、乙两人是否答对每个试题互不影响.
(1)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;
(2)若答对一题得5分,答错或不答得0分,记乙答题的得分为,求的分布列。
期中考试参考答案
一.选择题
BBCAD AADAA BA
二. 填空题
13. 36
14. 26
13. 240
14. 315
二. 解答题
17解:(1)不选0时,有个;选0时,0不能排在首位, ,根据分类计数原理,共有720+540=1260个四位数.
(2)①“1××5”,中间所缺的两数只能从0,2,4,6中选排,有个;
②“2××5",中间所缺的两数是奇偶数各一个,有个;
③“3××5",仿“1××5”,也有个;
④“4××5",仿“2××5",也有个;
⑤“6××5”也有个;
即小于7000的数共有96个,故第97个数是7025,第98个数是7045,第99个数是7065,第100个数是7205.
18.(1)的展开式的通项为.
令,得,即第7项为常数项.
,即常数项为.
(2)的展开式的通项为,
令,.
∴,∴.
(3)∵,
的展开式中含的项是:展开式中的一次项与展开式中的常数项之积;展开式中的常数项与展开式中的一次项之积.
∴的系数为.
19(1)记甲、乙两人击中丙没有击中为事件,则甲,乙两人击中,丙没有击中的概率为:;
(2)由题意可知,随机变量的可能取值为、、、,
,,
,.
所以,随机变量的分布列如下:
20.(1) ,73;(2).
21.(1),2019年该城市人均可支配月收入为1.236万元;(2)
22解:(1)参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试,在这8个试题中甲能答对6个,
甲通过自主招生初试的概率
参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试.
在这8个试题中乙能答对每个试题的概率为,
乙通过自主招生初试的概率
,甲通过自主招生初试的可能性更大.
(2)根据题意,乙答对题的个数的可能取值为0,1,2,3,4.
且
的概率分布列为:
0
5
10
15
20