2012年数学湖南省高考压轴卷文 21页

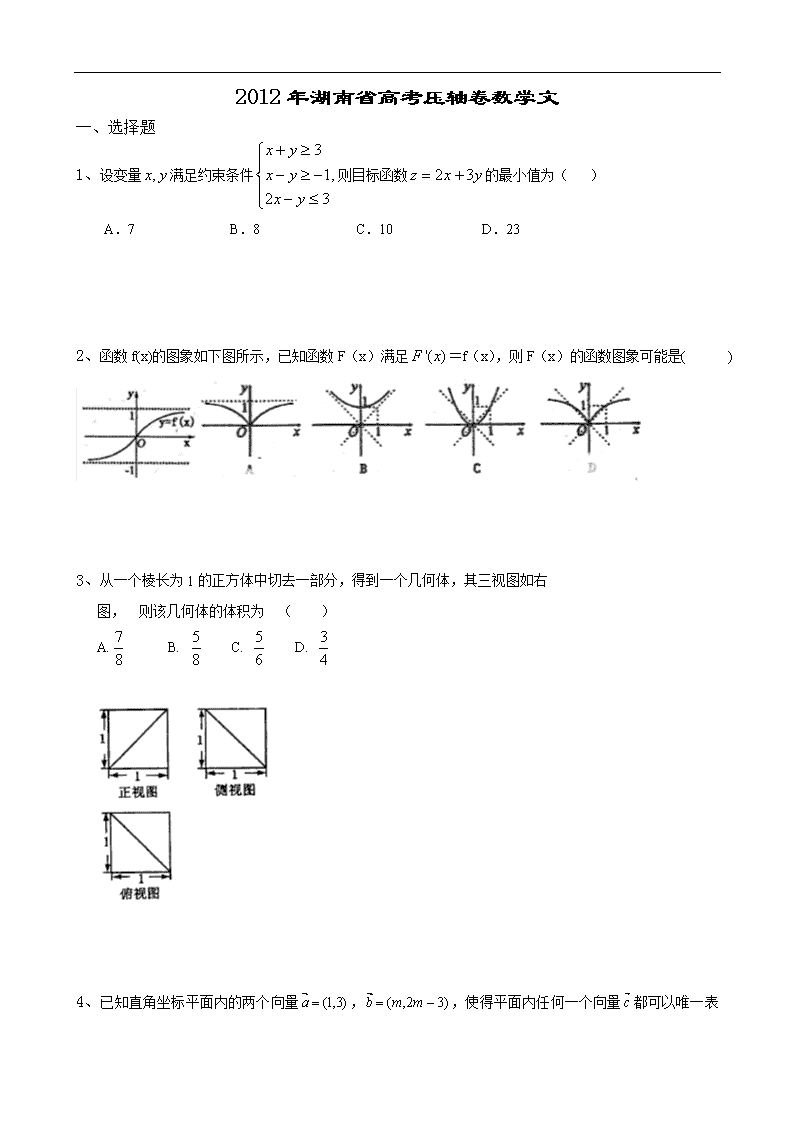
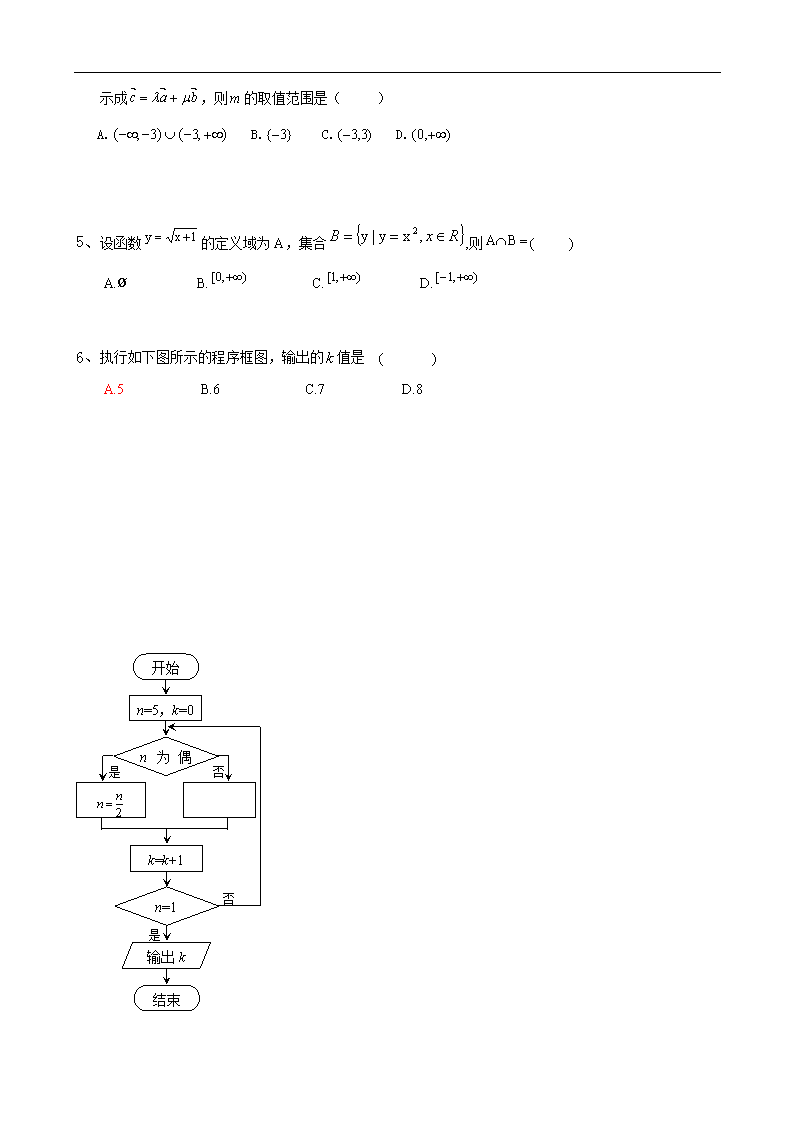
‎2012年湖南省高考压轴卷数学文 一、选择题 ‎1、设变量满足约束条件则目标函数的最小值为（ ） ‎ ‎ A．7 B．‎8 ‎C．10 D．23‎ ‎2、函数f(x)的图象如下图所示，已知函数F（x）满足＝f（x），则F（x）的函数图象可能是( )‎ ‎3、从一个棱长为1的正方体中切去一部分，得到一个几何体，其三视图如右 ‎ 图， 则该几何体的体积为 （ ）‎ A. B. C. D. ‎ ‎4、已知直角坐标平面内的两个向量，，使得平面内任何一个向量 都可以唯一表示成，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎5、设函数的定义域为A，集合,则( )‎ ‎ A.ø B. C. D.‎ ‎6、执行如下图所示的程序框图，输出的值是 ( ) ‎ A.5 B‎.6 C.7 D.8 ‎ 开始 n=5，k=0‎ n为偶数 n=1‎ 输出k 结束 k=k+1‎ 是 否 是 否 ‎7、已知圆x2＋y2=9与圆x2＋y2－4x＋4y－1=0关于直线l对称，则直线l的方程为( )‎ A．4x－4y＋1=0 B．x－y=0 ‎ C．x＋y=0 D．x－y－2=0‎ ‎8、把复数z的共轭复数记作，i为虚数单位．若z＝1＋i，则(1＋z)·＝(　　)‎ A．3－i B．3＋i C．1＋3i D．3‎ ‎9、已知集合U=R，集合等于（ ） ‎ ‎ A B ‎ ‎ C D ‎ ‎10、设x，y∈R，则“x≥2且y≥‎2”‎是“x2＋y2≥‎4”‎的(　　)‎ A．充分而不必要条件　　 　　 B．必要而不充分条件 C．充分必要条件　　　　　　　　 D．即不充分也不必要条件 ‎11、 某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程＝x＋中的为9.4，据此模型预报广告费用为6万元时销售额为(　　)‎ A．63.6万元 　　 B．65.5万元　　　C．67.7万元 　　　 D．72.0万元 ‎12、已知数列{}满足，且，则的值是（ ）‎ A. B. C.5 D. ‎ ‎13、下列说法正确的是 （ ）‎ ‎ A．函数图象的一条对称轴是直线 ‎ B．若命题，则命题 ‎ C．“a=‎1”‎是“直线与直线互相垂直”的充要条件 ‎ D．若 ‎14、将一骰子抛掷两次，所得向上的点数分别为和，则函数在上为增函数的概率是（ ） ‎ ‎ A． B． C． D．‎ ‎15、已知为虚数单位，则在复平面内对应的点位于( )‎ ‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎16、设函数f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)的最小正周期为π，且f(－x)＝f(x)，则(　　)‎ A．f(x)在单调递减 B．f(x)在单调递减　‎ C．f(x)在单调递增 D．f(x)在单调递增 ‎17、在等差数列则此数列前13项的和为（ ）‎ A．13 B．‎26 ‎C．52 D．156 ‎ ‎18、阅读右面的程序框图，运行相应的程序，则输出i的值为(　　)‎ A．3 B．‎4 C．5 D．6‎ 二、填空题 ‎19、(优选法与试验设计初步) 用0.618法寻找实验的最优加入量时，若当前存优范围是[628，774]，好点是718，则此时要做试验的加入点值是 。‎ ‎20、定义在R上的奇函数满足：则= 。‎ ‎21、有一个底面圆半径为1、高为2的圆柱，点O为这个圆柱底面圆的圆心，在这个圆柱内随机取一点P，则点P到点O的距离大于1的概率为　　　.‎ ‎22、已知满足，则的最大值为 ．‎ ‎23、设斜率为2的直线过抛物线的焦点F，且和y轴交于点A，若（O为坐标原点）的面积为4，则抛物线方程为 。‎ ‎24、函数，其中是常数，其图像是一条直线，称这个函数为线性函数，而对于非线性可导函数，在已知点附近一点的函数值可以用下面方法求其近似代替值，，利用这一方法，对于实数，取的值为4，则m的近似代替值是 。‎ ‎25、 在平面直角坐标系xOy中，椭圆C的中心为原点，焦点F1， F2在x轴上，离心率为.过F1‎ 的直线l交C于A，B两点，且△ABF2的周长为16，那么C的方程为________‎ ‎26、已知向量a、b的夹角为,|a|=2, |b|=3,则|‎2a－b |= ．‎ ‎27、 下列四种说法 ‎①命题“＞0”的否定是“”；‎ ‎②“命题为真”是“命题为真”的必要不充分条件；‎ ‎③“若＜，则＜”的逆命题为真；‎ ‎④若实数，则满足：＞1的概率为；‎ 正确的有___________________.（填序号）‎ ‎28、. 已知，则不等式的解集是_________.‎ ‎29、(坐标系与参数方程) 已知曲线C的极坐标方程为，则曲线C上的点到直线为参数）的距离的最大值为 . ‎ ‎30、 某班级有50名学生，现要采取系统抽样的方法在这50名学生中抽出10名学生，将这50名学生随机编号1—50号，并分组，第一组1—5号，第二组6—10号，……，第十组46—50号，若在第三组中抽得号码为12的学生，则在第八组中抽得号码为___ 的学生.‎ ‎31、某几何体的三视图，其中正视图是腰长为的等腰三角形,侧视图是半径为1的半圆，则该几何体的表面积是 .‎ ‎32、 函数 ‎(1) 若a=0,则方程f(x)=0的解为_______.‎ ‎(2) 若函数f(x)有两个零点，则a的取值范围是_______.‎ 三、解答题 ‎33、已知在数列{an}中，（t>0且t≠1）．是函数的一个极值点．‎ ‎ （1）证明数列是等比数列，并求数列的通项公式；‎ ‎ （2）记，当t=2时，数列的前n项和为Sn，求使Sn>2012的n的最小值；‎ ‎ （3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．‎ ‎34、‎ 已知函数.‎ ‎（Ⅰ）求的单调递增区间；‎ ‎（Ⅱ）在中，角，，的对边分别为. 已知，，试判断的形状.‎ ‎35、‎ 现对某市工薪阶层关于“楼市限购政策”的态度进行调查，随机抽查了50人，他们月收入（单位：百元）的频数分布及对“楼市限购政策”赞成人数如下表：‎ 月收入（单位百元）‎ ‎[15,25‎ ‎[25，35‎ ‎[35，45‎ ‎[45，55‎ ‎[55，65‎ ‎[65,75‎ 频数 ‎5‎ ‎10‎ ‎15‎ ‎10‎ ‎5‎ ‎5‎ 赞成人数 ‎4‎ ‎8‎ ‎12‎ ‎5‎ ‎2‎ ‎1‎ ‎（Ⅰ）根据以上统计数据填写下面2×2列联表，并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异？‎ 月收入不低于55百元的人数 月收入低于55百元的人数 合计 赞成 不赞成 合计 ‎（Ⅱ)若从月收入在[55，65）的被调查对象中随机选取两人进行调查，求至少有一人不赞成“楼市限购政策”的概率.‎ ‎（参考公式：，其中.）‎ 参考值表：‎ P()‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎36、‎ 如图，矩形中，，．，分别在线段和上，∥，将矩形沿折起．记折起后的矩形为，且平面平面．‎ ‎（Ⅰ）求证：∥平面；‎ ‎（Ⅱ）若，求证：； ‎ ‎（Ⅲ）求四面体体积的最大值． ‎ ‎37、‎ 已知椭圆的离心率为，其左、右焦点分别为，点是椭圆上一点，且，(为坐标原点).‎ ‎ (Ⅰ)求椭圆的方程；‎ ‎(Ⅱ)过点且斜率为的动直线交椭圆于两点，在轴上是否存在定点，使以为直径的圆恒过这个点?若存在，求出的坐标，若不存在，说明理由.‎ ‎38、已知圆的圆心为，半径为，圆与椭圆：有一个公共点(3,1)，分别是椭圆的左、右焦点．‎ ‎（1）求圆的标准方程；‎ ‎（2）若点P的坐标为(4,4)，试探究斜率为k的直线与圆能否相切，若能，求出椭圆和直线的方程;若不能，请说明理由．‎ ‎39、 在△中， 的对边分别是，且满足.‎ ‎（1）求；‎ ‎（2）设的最大值是5，求的值.‎ ‎40、 等比数列{an}的各项均为正数，且‎2a1＋‎3a2＝1，a＝‎9a2a6.‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设bn＝log‎3a1＋log‎3a2＋…＋log3an，求数列的前n项和．‎ ‎41、 已知向量，从6张大小相同、分别标有号码1、2、3、4、5、6的卡片有放回地抽取两张，x、y分别表示第一次、第二次抽取的卡片上的号码.‎ ‎（1）求满足的概率；‎ ‎（2）求满足的概率．‎ ‎42、 长沙市“两会”召开前，某政协委员针对自己提出的“环保提案”对某处的环境状况进行了实地调研.据测定，该处的污染指数与附近污染源的强度成正比，与到污染源的距离成反比，比例常数为k(k＞0).现已知相距‎36 km的A，B两家化工厂(污染源)的污染强度分别为正数a,b，它们连线上任意一点C处的污染指数y等于两化工厂对该处的污染指数之和.设AC=x(km).‎ ‎ (Ⅰ) 试将y表示为x的函数； ‎ ‎ (Ⅱ) 若a=1时，y在x=6处取得最小值，试求b的值.‎ 以下是答案 一、选择题 ‎1、A ‎ ‎2、 B ‎3、 C ‎4、 A ‎5、 B ‎6、 A ‎7、 D ‎8、A ‎ ‎9、A ‎ ‎10、A ‎11、B ‎ ‎12、B ‎13、 A ‎14、D ‎15、 D ‎16、A ‎ ‎17、 B ‎18、B ‎ 二、填空题 ‎19、 684 ‎ ‎20、 ‎ ‎21、 ‎ ‎22、 3 ‎ ‎23、 ‎ ‎24、 2.0005 ‎ ‎25、 .＋＝1.‎ ‎26、 ‎ ‎27、 ①②‎ ‎28、 (-∞, 1〕‎ ‎29、 ‎ ‎30、 37‎ ‎31、 ‎ ‎32、 (1)‎ ‎(2)‎ 三、解答题 ‎33、（1）．‎ 由题意，即． ‎ ‎∴‎ ‎∵且，∴数列是以为首项，t为公比的等比数列，‎ ‎ ‎ 以上各式两边分别相加得，∴，‎ 当时，上式也成立，∴ ‎ ‎ （2）当t=2时，‎ ‎ ‎ ‎ ‎ 由，得，‎ ‎， ‎ 当，‎ 因此n的最小值为1005． ‎ ‎ （3）∵‎ 令，则有：‎ 则 ‎ ‎ 即函数满足条件．‎ ‎ ‎ ‎34、解：（Ⅰ） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎. ‎ 由， ‎ 得：. ‎ 所以 的单调递增区间为，. ‎ ‎（Ⅱ）因为 ，‎ 所以 .所以. ‎ 因为 ，所以 . ‎ 所以 . ‎ 因为 ，，‎ 所以 . ‎ 因为 ，，所以 .所以 . ‎ ‎35、解:（Ⅰ）根据题目得2×2列联表：‎ 月收入不低于55百元人数 月收入低于55百元人数 合计 赞成 ‎32‎ 不赞成 ‎18‎ 合计 ‎10‎ ‎40‎ ‎50‎ 假设月收入以5500为分界点对“楼市限购政策” 的态度没有差异，根据列联表中的数据，得到：‎ 假设不成立.‎ 所以没有99%的把握认为月收入以5500元为分界点对“楼市限购政策”的态度有差异 ‎（Ⅱ）设此组五人为,其中表示赞同者，表示不赞同者 从中选取两人的所有情形为：‎ 其中至少一人赞同的有7种，故所求概率为 ‎36、（Ⅰ）证明：因为四边形，都是矩形，‎ ‎ 所以 ∥∥，．‎ ‎ 所以 四边形是平行四边形，‎ ‎ 所以 ∥， ‎ ‎ 因为 平面，‎ 所以 ∥平面． ‎ ‎（Ⅱ）证明：连接，设．‎ 因为平面平面，且， ‎ 所以 平面， ‎ 所以 ． ‎ 又 ， 所以四边形为正方形，所以 ． ‎ 所以 平面， ‎ 所以 ． ‎ ‎（Ⅲ）解：设，则，其中．‎ 由（Ⅰ）得平面，‎ 所以四面体的体积为． ‎ 所以 ． ‎ 当且仅当，即时，四面体的体积最大． ‎ ‎37、解：（Ⅰ）因为，所以. ‎ ‎∵，∴⊥，∴；‎ 又∵，∴，‎ ‎∴.b=1. 因此所求椭圆的方程为： ‎ ‎ ‎ y F1‎ F2‎ x S O A B ‎ (Ⅱ)动直线的方程为：‎ 由得 设 则 ‎ 假设在y轴上存在定点M（0，m），满足题设，则 ‎ ‎ 由假设得对于任意的恒成立，‎ 即 解得m=1.‎ 因此，在y轴上存在定点M，使得以AB为直径的圆恒过这个点，‎ 点M的坐标为（0，1）‎ ‎38、 解：（1）由已知可设圆C的方程为 ．‎ 将点A的坐标代入圆C的方程，得 ，‎ 即，解得．‎ ‎∵，∴，∴圆C的方程为 ． ‎ ‎（2）直线能与圆C相切.‎ 依题意，设直线的方程为，即.‎ 若直线与圆C相切，则，‎ ‎∴，解得.‎ 当时，直线与x轴的交点横坐标为，不合题意，舍去；‎ 当时，直线与x轴的交点横坐标为，‎ ‎∴，‎ ‎∴由椭圆的定义得 ‎，‎ ‎∴，即， ∴， ‎ 直线能与圆C相切，直线的方程为，椭圆E的方程为 ．‎ ‎39、解：（1）， ，‎ 即.‎ ‎ .‎ ‎（2）， ‎ 设则.，．‎ 当时，取最大值.依题意得，.‎ ‎40、解：（1）设（x,y）表示一个基本事件，则两次抽取卡片的所有基本事件有(1,1)、 (1,2)、(1,3)、(1,4)、(1,5)、(1,6)、(2,1)、(2,2)、 …、(6,5)、(6,6)，共36个．‎ 用A表示事件“”，即,则Ａ包含的基本事件有(1,1)、(3,2)、(5,3)共3个，．‎ ‎（2）在（1）中的36个基本事件中，满足的事件有（3，1）、（4，1）、（5、1）、（6，1）、（5，2）、（6、2）共6个，所以P（B）＝．‎ ‎41、解：(1)设数列{an}的公比为q，由a＝‎9a2a6得a＝‎9a，所以q2＝.‎ 由条件可知q＞0，故q＝.‎ 由‎2a1＋‎3a2＝1得‎2a1＋‎3a1q＝1，所以a1＝.‎ 故数列{an}的通项公式为an＝.‎ ‎(2)bn＝log‎3a1＋log‎3a2＋…＋log3an ‎＝－(1＋2＋…＋n)‎ ‎＝－.‎ 故＝－＝－2，‎ ＋＋…＋＝－2＝－.‎ 所以数列的前n项和为－.‎ ‎42、解：（Ⅰ） 设点C受A污染源污染指数为，点C受B污染源污染指数为，其中k为比例系数，且k＞0. ‎ 从而点C处污染指数 ‎（Ⅱ） 因为a=1，所以，，‎ y′=，‎ 令y′=0，得，‎ 当x∈时，函数单调递减；当x∈时，函数单调递增.‎ ‎∴当时，函数取得最小值 又此时x=6，解得b=25，经验证符合题意.‎ 所以，污染源B的污染强度b的值为25‎