- 614.67 KB
- 2021-06-02 发布
考点一 平面向量的数量积
考点清单
考向基础
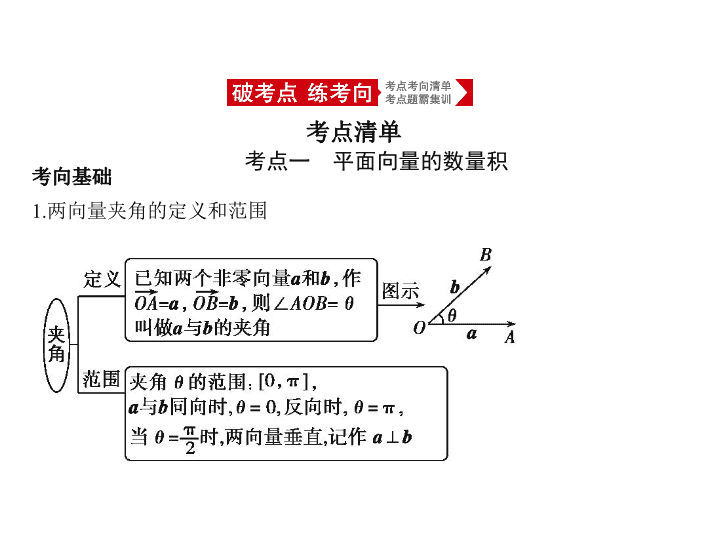
1.两向量夹角的定义和范围
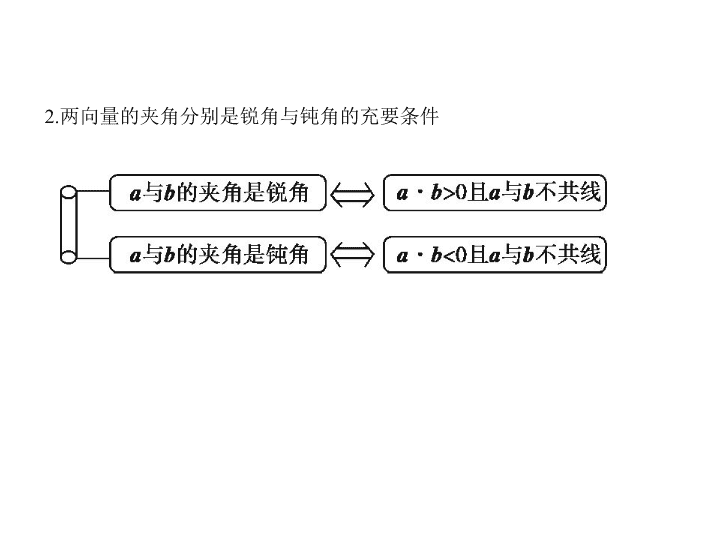
2.两向量的夹角分别是锐角与钝角的充要条件
3.平面向量的数量积
4.向量数量积的性质
设
a
,
b
都是非零向量,
e
是与
b
方向相同的单位向量,
θ
是
a
与
e
的夹角,则
(1)
e
·
a
=
a
·
e
=
|
a
|·cos
θ
.
(2)当
a
与
b
同向时,
a
·
b
=|
a
||
b
|
;当
a
与
b
反向时,
a
·
b
=-|
a
||
b
|
.
特别地,
a
·
a
=|
a
|
2
.
(3)
|
a
·
b
|
≤
|
a
|·|
b
|
.
5.坐标表示
若
a
=(
x
,
y
),则
a
·
a
=
a
2
=|
a
|
2
=
x
2
+
y
2
,|
a
|=
.
考向一 求平面向量的数量积
考向突破
例1 (1)(2020届皖南八校摸底考试,5)已知
=(-3,-2),
=(
m
,1),|
|=3,则
·
=
( )
A.7 B.-7 C.15 D.-15
(2)(命题标准样题,13)设△
ABC
中
AC
=1,
AB
=2,∠
CAB
=60
°
,
=
a
,
=
b
,
=
c
,则
a
·
b
+
b
·
c
+
c
·
a
=
.
解析 (1)
=
-
=(
m
+3,3),∵|
|=3,∴(
m
+3)
2
+9=9,∴
m
=-3,∴
=(-3,
1),∵
=(3,2),∴
·
=-9+2=-7.
(2)试题考查平面向量的概念、运算、平面向量数量积等数学知识.试题解
法灵活多样,考查化归与转化的数学思想,体现了理性思维的学科素养.考
查了逻辑推理能力、运算求解能力,落实了基础性的考查要求.
a
·
b
+
b
·
c
+
c
·
a
=
b
·(
a
+
c
)+
c
·
a
=-(
a
+
c
)
2
+
c
·
a
=-
a
2
-
c
·
a
-
c
2
=-4.
答案 (1)B (2)-4
考向二 求平面向量的投影
例2 (2020届贵州遵义摸底考试,6)已知向量
a
,
b
的夹角为60
°
,且|
a
|=|
b
|=2,则
向量
a
-
b
在向量
a
方向上的投影为
( )
A.-1 B.1 C.2 D.3
解析 设向量
a
-
b
与向量
a
的夹角为
θ
,则向量
a
-
b
在向量
a
方向上的投影为|
a
-
b
|cos
θ
=|
a
-
b
|·
=
=
=
=1,故选B.
答案 B
考点二 平面向量数量积的应用
考向基础
1.向量数量积的应用
已知
a
=(
x
1
,
y
1
),
b
=(
x
2
,
y
2
).
(1)证明垂直问题,常用向量垂直的充要条件,
a
⊥
b
⇔
a
·
b
=0
⇔
x
1
x
2
+
y
1
y
2
=0
.
(2)求解夹角问题,常利用夹角公式:
cos
θ
=
=
(其中
θ
为
a
与
b
的夹角).
(3)求线段长度问题,常利用向量的长度公式:
|
a
|=
=
或|
|=
.
在△
ABC
中,∠
A
,∠
B
,∠
C
所对的边分别为
a
,
b
,
c
.
(1)在
=
λ
的条件下,存在
λ
使得
I
为△
ABC
的内心;
a
+
b
+
c
=0
⇔
P
为△
ABC
的内心.
(2)|
|=|
|=|
|
⇔
P
为△
ABC
的外心.
(3)
+
+
=0
⇔
G
为△
ABC
的重心.
(4)
·
=
·
=
·
⇔
P
为△
ABC
的垂心.
2.向量中常用的结论
考向一 求平面向量的夹角
考向突破
例3 (2020届广西桂林十八中8月月考,6)已知向量
a
,
b
满足|
a
|=
,|
b
|=1,且
|
b
+
a
|=2,则向量
a
与
b
的夹角的余弦值为
( )
A.
B.
C.
D.
解析 由|
b
+
a
|=2得(
b
+
a
)
2
=4,即
a
2
+2
a
·
b
+
b
2
=4.又∵|
a
|=
,|
b
|=1,∴2+2
a
·
b
+1=
4,解得
a
·
b
=
.设向量
a
与
b
的夹角为
θ
,则有cos
θ
=
=
=
=
,故选
D.
答案 D
例4 (2018湖南永州二模,4)已知非零向量
a
,
b
的夹角为60
°
,且|
b
|=1,|2
a
-
b
|=
1,则|
a
|=
( )
A.
B.1 C.
D.2
考向二 求平面向量的模
解析 ∵非零向量
a
,
b
的夹角为60
°
,且|
b
|=1,
∴
a
·
b
=|
a
|
×
1
×
=
.
∵|2
a
-
b
|=1,
∴|2
a
-
b
|
2
=4
a
2
-4
a
·
b
+
b
2
=4|
a
|
2
-2|
a
|+1=1,
∴4|
a
|
2
-2|
a
|=0,
∴|
a
|=
(|
a
|=0舍去),故选A.
答案 A
方法1
平面向量的模的求解方法
利用向量数量积求解向量的长度问题是向量数量积的重要应用,要掌握此
类问题的处理方法:
1.
a
2
=
a
·
a
=|
a
|
2
或
|
a
|=
.
2.|
a
±
b
|=
=
.
3.若
a
=(
x
,
y
),则
|
a
|=
或|
a
|
2
=
x
2
+
y
2
.
方法技巧
例1 已知点
A
(4,3)和点
B
(1,2),点
O
为坐标原点,则|
+
t
|(
t
∈R)的最小值
为
( )
A.5
B.5 C.3 D.
解析 由题意可得
=(4,3),
=(1,2),
∴
+
t
=(4+
t
,3+2
t
),
∴|
+
t
|=
=
=
,
∵
t
∈R,∴当
t
=-2时,|
+
t
|取得最小值
,故选D.
答案 D
方法2
平面向量夹角的求解方法
1.定义法:利用向量数量积的定义知,cos
θ
=
,其中两个向量的夹角θ∈
[0,π],求解时应求出三个量:
a
·
b
,|
a
|,|
b
|或找出这三个量之间的关系.
2.坐标法:若
a
=(
x
1
,
y
1
),
b
=(
x
2
,
y
2
),
θ
为
a
,
b
的夹角,则cos
θ
=
.
3.三角函数法:可以把所求两向量的夹角放到三角形中,利用正、余弦定理
和三角形的面积公式等知识进行求解.
例2 (2020届江西南昌三校期初调研,6)若非零向量
a
,
b
满足|
a
|=
|
b
|,且
(
a
-
b
)⊥(3
a
+2
b
),则
a
与
b
的夹角为
( )
A.
B.
C.
D.π
解析 由(
a
-
b
)⊥(3
a
+2
b
),得(
a
-
b
)·(3
a
+2
b
)=0,
即3
a
2
-
a
·
b
-2
b
2
=0,又知|
a
|=
|
b
|,
∴
a
·
b
=3
a
2
-2
b
2
=3
×
|
b
|
2
-2|
b
|
2
=
|
b
|
2
.
设
a
与
b
的夹角为
θ
,则cos
θ
=
=
=
,
又知
θ
∈[0,π],∴
θ
=
,即
a
与
b
的夹角为
.
答案 A
方法3
用向量法解决平面几何问题
1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系,
用向量表示问题中涉及的几何元素,将平面几何问题转化为向量的问题;
②通过向量运算研究几何元素之间的关系,如距离、夹角等问题;③把运算
结果转化成几何关系.
2.用向量法解平面几何问题,主要是
通过建立平面直角坐标系将问题坐标
化,
然后利用平面向量的坐标运算求解有关问题,这样可以避免繁杂的逻辑
推理,同时加强了数形结合思想在解题中的应用.
例3 在平行四边形
ABCD
中,
AD
=1,∠
BAD
=60
°
,
E
为
CD
的中点.若
·
=
1,则
AB
的长为
.
解析 解法一:由题意可知,
=
+
,
=-
+
.
因为
·
=1,所以(
+
)·
=1,
即
+
·
-
=1.
①
因为|
|=1,∠
BAD
=60
°
,
所以
·
=
|
|,
因此①式可化为1+
|
|-
|
|
2
=1.
解得|
|=0(舍去)或|
|=
,
所以
AB
的长为
.
解法二:以
A
为原点,
AB
所在直线为
x
轴建立如图所示的直角坐标系,过
D
作
DM
⊥
AB
于点
M
.
由
AD
=1,∠
BAD
=60
°
,可知
AM
=
,
DM
=
,
∴
D
.
设|
|=
m
(
m
>0),则
B
(
m
,0),
C
,
因为
E
是
CD
的中点,所以
E
.
所以
=
,
=
.
由
·
=1可得
+
=1,
即2
m
2
-
m
=0,所以
m
=0(舍去)或
m
=
.
故
AB
的长为
.
答案