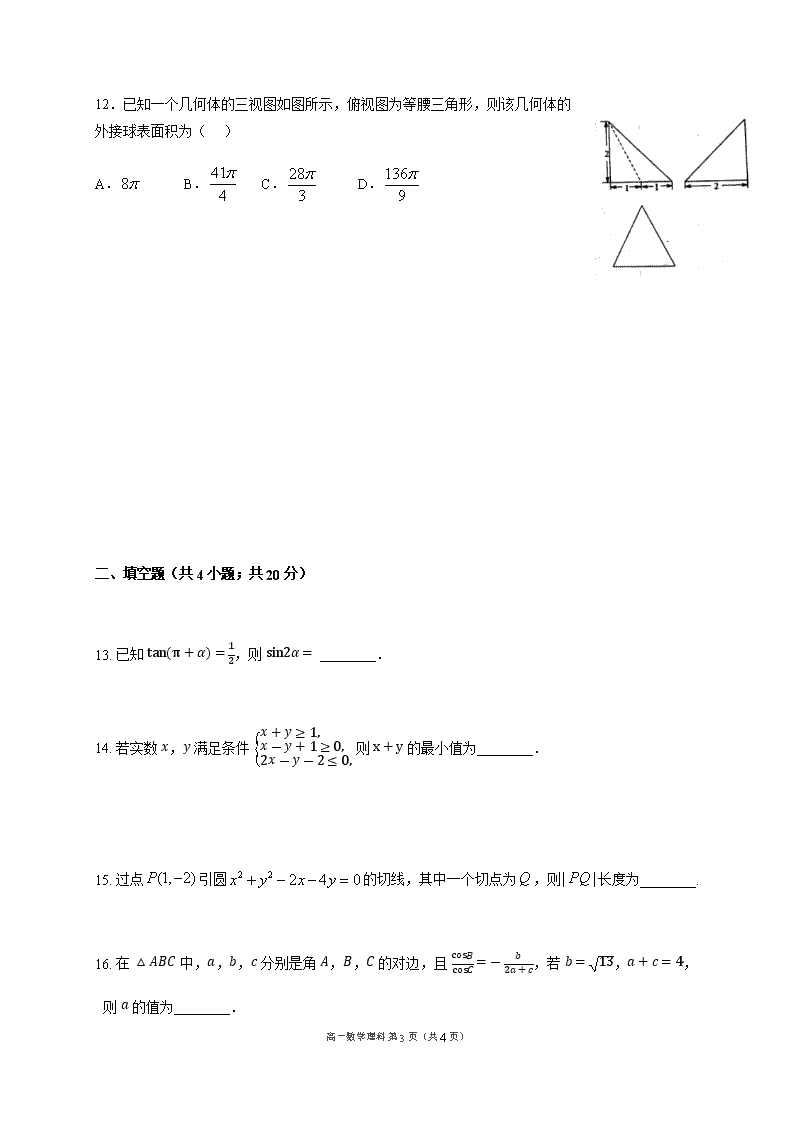四川省成都外国语学校2019-2020学年高一下学期期末考试数学（理）试题 12页

成都外国语学校 2019~2020学年下期末考试 高一理科数学 ‎ ‎ 一、选择题（共12小题；共60分）‎ ‎1. 计算（ ）‎ A. B. C. D. ‎ ‎2. 在等差数列 an 中，若 a‎3‎‎=-5‎，a‎5‎‎=-9‎，则 a‎7‎‎=‎ ‎（‎ ）‎ ‎ A. ‎-12‎ B. ‎-13‎ C. ‎12‎ D. ‎‎13‎ ‎3. 已知直线与平行.则实数的值（ ）‎ A.2 B. C. D. 或2 ‎ ‎ ‎ ‎4. 若，且，则下列不等式中一定正确的是（ ）‎ A. B. C. D. ‎ ‎5. 在 ‎△ABC 中，若 acosA‎=bcosB=‎ccosC，则 ‎△ABC 是 （ ）‎ ‎ A. 直角三角形 B. 等边三角形 ‎ C. 钝角三角形 D. 等腰直角三角形 ‎6. 已知等比数列 an 的各项都为正数，且 a‎3‎，‎1‎‎2‎a‎5‎，a‎4‎ 成等差数列，则 a‎3‎‎+‎a‎5‎a‎4‎‎+‎a‎6‎ 的值是 （ ）‎ ‎ A. ‎5‎‎-1‎‎2‎ B. ‎5‎‎+1‎‎2‎ C. ‎3-‎‎5‎‎2‎ D. ‎‎3+‎‎5‎‎2‎ 高一数学理科 第12页（共4页）‎ ‎7．已知一个正三棱锥的高为3，如下图是其底面用斜二测画法所画出的水平放置的直观图，其中，则此正三棱锥的体积为（ ）‎ A． B． C． D．‎ ‎8．已知直线恒过定点A,点A也在直线上，其中均为正数，则的最小值为（ ） ‎ A．2 B.4 C． 6 D． 8‎ ‎9. 如图，在 ‎△ABC 中，D 是边 AC 上的点，且 AB=AD， ‎2AB=‎3‎BD，BC=2DB，则 sinC 的值为 （ ）‎ ‎ A. ‎3‎‎3‎ B. ‎3‎‎6‎ C. ‎6‎‎3‎ D. ‎‎6‎‎6‎ ‎ ‎ ‎10. 满足, 的恰有一个, 那么的取值范围是( )‎ A. B. ‎ C. D. 或 ‎ ‎ ‎11. 如图，圆与轴相切于点，与轴正半轴交于两点（B在A的上方），且．过点任作一条直线与圆相交于两点，的值为（ ）‎ A.2 B. 3 C. D.‎ ‎ ‎ 高一数学理科 第12页（共4页）‎ ‎12．已知一个几何体的三视图如图所示，俯视图为等腰三角形，则该几何体的外接球表面积为（ ）‎ A． B． C． D．‎ ‎ ‎ 二、填空题（共4小题；共20分）‎ ‎13. 已知 tanπ+α=‎‎1‎‎2‎，则 sin2α=‎  ．‎ ‎ ‎ ‎14. 若实数 x，y 满足条件 x+y≥1,‎x-y+1≥0,‎‎2x-y-2≤0,‎ 则 x+y 的最小值为  ．‎ ‎ ‎ ‎15. 过点引圆的切线，其中一个切点为，则长度为________.‎ ‎16. 在 ‎△ABC 中，a，b，c 分别是角 A，B，C 的对边，且 cosBcosC‎=-‎b‎2a+c，若 b=‎‎13‎，a+c=4‎，‎ 则 a 的值为  ．‎ 高一数学理科 第12页（共4页）‎ ‎ ‎ 三、解答题（共6小题；共78分）‎ ‎17. 已知．‎ ‎（1）求的值；‎ ‎（2）求的值．‎ ‎ ‎ ‎18. 已知函数 fx=2sinx+‎π‎3‎cosx．‎ ‎（1）若 ‎0≤x≤‎π‎2‎，求函数 fx 的值域；‎ ‎（2）设 ‎△ABC 的三个内角 A，B，C 所对的边分别是 a，b，c．若 A 为锐角且 fA=‎‎3‎‎2‎，b=2‎，c=3‎．求 cosA-B 的值．‎ ‎ ‎ ‎19. 已知关于直线对称，‎ 且圆心在轴上.‎ ‎（1）求的标准方程；‎ ‎（2）已知动点在直线上，过点引的两条切线、，切点分别为.‎ 高一数学理科 第12页（共4页）‎ 记四边形的面积为，求的最小值；‎ ‎ ‎ ‎20. 设等差数列 an 的前 n 项和为 Sn，且 S‎4‎‎=4‎S‎2‎，a‎2‎‎=2a‎1‎+1‎．‎ ‎（1）求数列 an 的通项公式；‎ ‎（2）设数列 bn 前 n 项和为 Tn，且 Tn‎+an‎+1‎‎2‎n=0‎．令 cn‎=‎b‎2nn∈‎N‎*‎．‎ 求数列 cn 的前 n 项和 Rn．‎ ‎ ‎ 高一数学理科 第12页（共4页）‎ ‎21. 已知中，角，，所对的边分别为，，，，且满足.‎ ‎（1）求的面积；‎ ‎（2）若，求的最大值.‎ ‎ ‎ ‎22. 已知数列满足，‎ ‎（1）求，的值；‎ ‎（2）求证：数列是等比数列，并求的通项公式；‎ ‎（3）设，若不等式‎15(1+‎1‎b‎1‎)(1+‎1‎b‎2‎)⋯(1+‎1‎bn)≥k‎10n+15‎对于 任意都成立，求正数的最大值.‎ 高一数学理科 第12页（共4页）‎ 高一数学理科答案 第一部分 ‎1、A 2、B 3、A 4、C 5、B 6、B ‎7、A 8、D 9、D 10、D 11、C 12、B 第二部分 ‎13. ‎‎4‎‎5‎ ‎14. 1‎ ‎【解析】根据实数 x，y 满足条件 x+y≥1,‎x-y+1≥0,‎‎2x-y-2≤0‎ 画出可行域，‎ ‎15. ‎ ‎16. ‎1‎ 或 ‎‎3‎ ‎【解析】cosBcosC‎=-‎b‎2a+c，‎ 即有 ‎-2acosB=bcosC+ccosB，‎ 即 ‎-2sinAcosB=sinBcosC+cosCsinB=sin B+C ‎=sinA，‎ 即有 cosB=-‎‎1‎‎2‎，‎ 由于 B 为三角形的内角，则 B=‎‎2π‎3‎，‎ 又 b‎2‎‎=a‎2‎+c‎2‎-2accosB，即有 ‎13=a‎2‎+c‎2‎+ac，‎ 又 a+c=4‎，‎ 解得，a=1‎，c=3‎ 或 a=3‎，c=1‎．‎ ‎16. ‎‎1‎‎4‎ ‎【解析】设向量 a，b 的夹角为 θ，‎0‎‎∘‎‎<θ<‎‎90‎‎∘‎，‎ 因为 ‎∣x+2y∣≤‎‎8‎‎15‎，‎ 高一数学理科 第12页（共4页）‎ 所以 ‎1≥‎15‎‎8‎∣x+2y∣‎．‎ 又 ‎∣xa+yb∣=1‎，则 x‎2‎‎+y‎2‎+2xycosθ=1‎，‎ 所以 cosθ=‎1-x‎2‎-‎y‎2‎‎2xy≥‎15‎‎8‎x+2y‎2‎‎-x‎2‎-‎y‎2‎‎2xy=‎‎-‎49‎‎64‎x‎2‎-‎1‎‎16‎y‎2‎+‎15‎‎16‎xy‎2xy 恒成立，‎ 因为 ‎-‎49‎‎64‎x‎2‎-‎1‎‎16‎y‎2‎+‎15‎‎16‎xy‎2xy‎=‎15‎‎32‎-‎1‎‎2‎‎49x‎64y‎+‎y‎16x≤‎15‎‎32‎-‎7‎‎8×4‎=‎‎1‎‎4‎，‎ 所以 cosθ≥‎‎1‎‎4‎．即 a‎⋅‎b 的最小值为 ‎1‎‎4‎．‎ 第三部分 ‎17（1）由 所以．‎ 则 ‎（2）因为，．‎ 所以 ‎18. （1） fx=sin‎2x+‎π‎3‎+‎‎3‎‎2‎，fx∈‎‎0,1+‎‎3‎‎2‎ .‎ ‎      （2） A=‎π‎3‎，a=‎‎7‎，sinB=‎‎21‎‎7‎，cosB=‎‎2‎‎7‎‎7‎，cosA-B=‎‎5‎‎7‎‎14‎．‎ ‎19. （1）由题意知，‎ 圆心在直线上，即，‎ 高一数学理科 第12页（共4页）‎ 又因为圆心在轴上，所以，‎ 由以上两式得：，，‎ 所以.‎ 故的标准方程为.‎ ‎（2）①如图，的圆心为，半径，‎ 因为、是的两条切线，‎ 所以，，‎ 故 又因为，‎ 根据平面几何知识，要使最小，只要最小即可.‎ 易知，当点坐标为时，‎ ‎.‎ 此时.‎ ‎20. （1） 设等差数列 an 的首项为 a‎1‎，公差为 d，‎ 由 S‎4‎‎=4‎S‎2‎，a‎2n‎=2an+1‎ 得 ‎ ‎4a‎1‎+6d=8a‎1‎+4d,‎a‎1‎‎+‎2n-1‎d=2a‎1‎+2n-1‎d+1,‎ ‎ 解得 a‎1‎‎=1‎，d=2‎．‎ 因此 an‎=2n-1‎n∈‎N‎*‎．‎ ‎      （2） 由题意知：Tn‎=-‎n‎2‎n-1‎．‎ 高一数学理科 第12页（共4页）‎ 所以 n≥2‎ 时，bn‎=Tn-Tn-1‎=-n‎2‎n-1‎+‎n-1‎‎2‎n-2‎，‎ 故 cn‎=b‎2n=‎2n-2‎‎2‎‎2n-1‎=‎n-1‎‎1‎‎4‎n-1‎n∈‎N‎*‎，‎ 所以 Rn‎=0×‎1‎‎4‎‎0‎+1×‎1‎‎4‎‎1‎+2×‎1‎‎4‎‎2‎+3×‎1‎‎4‎‎3‎+⋯+n-1‎×‎‎1‎‎4‎n-1‎，‎ 则 ‎1‎‎4‎Rn‎=0×‎1‎‎4‎‎1‎+1×‎1‎‎4‎‎2‎+2×‎1‎‎4‎‎3‎+⋯+n-2‎×‎1‎‎4‎n-1‎+n-1‎×‎‎1‎‎4‎n，‎ 两式相减得 ‎ ‎ ‎3‎‎4‎Rn‎=‎1‎‎4‎‎1‎+‎1‎‎4‎‎2‎+‎1‎‎4‎‎3‎+⋯+‎1‎‎4‎n-1‎-n-1‎×‎‎1‎‎4‎n‎=‎1‎‎4‎‎-‎‎1‎‎4‎n‎1-‎‎1‎‎4‎-n-1‎‎1‎‎4‎n,‎ ‎ 整理得 Rn‎=‎‎1‎‎9‎‎4-‎‎3n+1‎‎4‎n-1‎，‎ 所以数列 cn 的前 n 项和 Rn‎=‎‎1‎‎9‎‎4-‎‎3n+1‎‎4‎n-1‎．‎ ‎21解：‎ ‎（1）在中，，∴‎ ‎∵‎ ‎∴‎ ‎∵，∴‎ ‎∴‎ ‎（2）∵‎ ‎∴‎ ‎∴‎ ‎∴‎ 高一数学理科 第12页（共4页）‎ ‎∴当时，取最大值.‎ ‎22. 解：（1）‎ ‎（2）证明：a‎1‎‎=2，an+1‎=3an+‎2‎n-1‎，n∈‎N‎*‎，‎ 可得an+1+2n＝3（an+2n﹣1），‎ 所以{an+2n﹣1}是以3为首项、3为公比的等比数列，所以an+2n﹣1＝3n，‎ 则an＝3n﹣2n﹣1，n∈N*；‎ ‎（3）bn＝log （3n﹣2n﹣1+2n﹣1）+1＝log3n+1＝2n+1，‎ 不等式‎(1+‎1‎b‎1‎)(1+‎1‎b‎2‎)⋯(1+‎1‎bn)≥‎m‎15‎‎2n+3‎，即m‎15‎‎≤‎(1+‎1‎b‎1‎)(1+‎1‎b‎2‎)⋯(1+‎1‎bn)‎‎2n+3‎=‎‎4‎‎3‎•‎6‎‎5‎•‎8‎‎7‎‎⋯‎‎2n+2‎‎2n+1‎•‎1‎‎2n+3‎，‎ 设f（n）‎=‎‎4‎‎3‎•‎6‎‎5‎•‎8‎‎7‎‎⋯‎‎2n+2‎‎2n+1‎•‎1‎‎2n+3‎，‎f(n+1)‎f(n)‎‎=‎‎4‎‎3‎‎⋅‎6‎‎5‎⋅‎8‎‎7‎⋯‎2n+2‎‎2n+1‎⋅‎2n+4‎‎2n+3‎⋅‎‎1‎‎2n+5‎‎4‎‎3‎‎⋅‎6‎‎5‎⋅‎8‎‎7‎⋯‎2n+2‎‎2n+1‎⋅‎‎1‎‎2n+3‎ ‎=‎‎2n+4‎‎2n+3‎‎•‎2n+3‎‎2n+5‎‎=‎2n+4‎‎(2n+3)(2n+5)‎=‎2n+4‎‎4n‎2‎+16n+15‎＞‎2n+4‎‎4n‎2‎+16n+16‎=‎2n+4‎‎(2n+4‎‎)‎‎2‎=‎1，‎ 所以f（n+1）＞f（n），即当n增大时，f（n）也增大，‎ 所以只需f（n）min即可．因为f（n）min＝f（1）‎=‎‎4‎‎3‎•‎1‎‎5‎‎=‎‎4‎‎5‎‎15‎，‎ 所以，即k≤4，‎ 所以正数k的最大值为4．‎ 高一数学理科 第12页（共4页）‎ 高一数学理科 第12页（共4页）‎